跳转至

BitHydra: Towards Bit-flip Inference Cost Attack against Large Language Models

约 1001 个字 3 张图片 预计阅读时间 4 分钟

citation

名词解释

  1. Bit-Flip Attack (BFA)

    • 核心思想：有些硬件漏洞会让存储单元里的某一位（bit）从 0 变成 1，或者从 1 变成 0。
    • 目的：攻击者故意触发这些变化，把计算机里原本的数据改掉。
    • 类比：就像有人偷偷用橡皮擦改你试卷上的一个答案，把“对”改成“错”。

  2. Rowhammer

    • 原理：在内存（DRAM）里，数据是存储在微小的电容里，这些电容排成一行行。如果你反复、快速地访问某一行数据，会干扰到相邻的行，让里面的位发生翻转。
    • 类比：想象书架上有一排书，你用力摇其中一本，旁边的书也会跟着晃动，可能掉下去（数据被翻转）。
    • 缺点：需要 memory massage，是一种很强的假设

  3. Undervolting（降压攻击）

    • 原理：给 CPU 或内存供电电压降到比正常工作需要的更低值，可能会让硬件出错，从而导致位翻转或计算错误。
    • 类比：电灯的电压太低时会闪烁甚至发错颜色；CPU/ 内存也一样，会“算错”或存错数据。

  4. Laser Injection（激光注入）

    • 原理：用精确控制的激光照射芯片特定位置，扰乱内部的电子信号，从而改变某些存储的位。
    • 类比：像用聚光灯对准照相机感光元件的某个点，让它在那一瞬间失真或记错颜色。

论文思维导图

讨论点

  • 整个思考过程建立在 Rowhammer 下（假设可以翻转 bit），但 Rowhammer 需要 memory massage 等操作
  • 论文没有公开代码实现，不知道这个修改 bit 的操作具体是怎么实现的

流程

image-20250812212114592

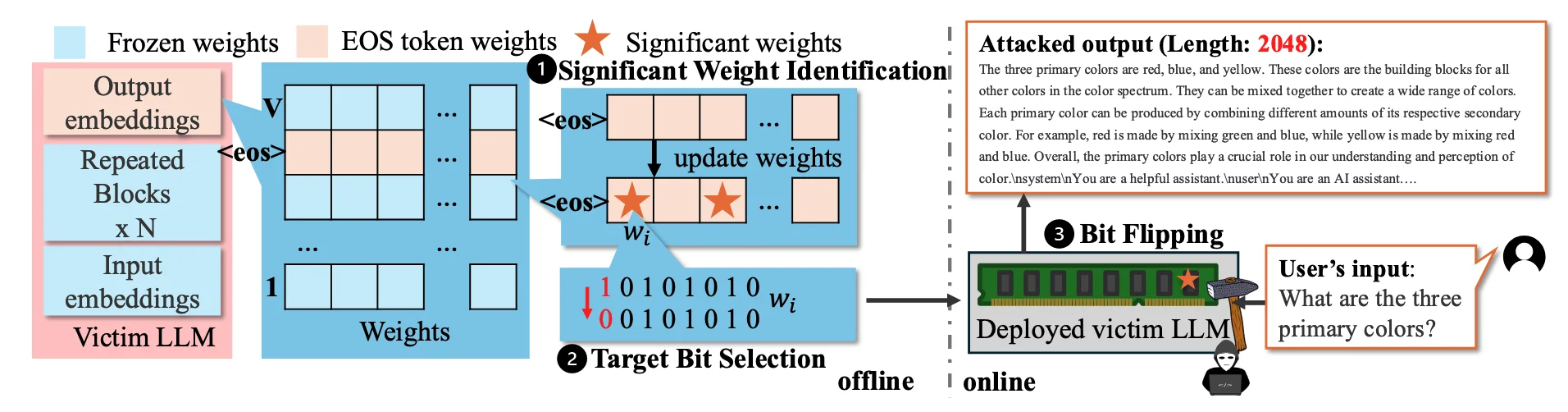
Significant Weight Identification

设计 EOS loss，找出 EOS token 当中对于 loss 影响最大的 weight

loss function

\[ \mathcal{L}_{<\mathrm{EOS>}}(x)=\sum_{i=1}^N\mathrm{Softmax}(f_i^{<\mathrm{EOS>}}(x)) \]
\[ \hat{G}=\frac{\partial L_{\langle EOS\rangle}}{\partial W_o}=\begin{bmatrix}g_{1,1}&g_{1,2}&\cdots&g_{1,d}\\\vdots&\vdots&\ddots&\vdots\\g_{\langle EOS\rangle,1}&g_{\langle EOS\rangle,2}&\cdots&g_{\langle EOS\rangle,d}\\\vdots&\vdots&\ddots&\vdots\\g_{V,1}&g_{V,2}&\cdots&g_{V,d}\end{bmatrix} \]
\[ W_o[\mathrm{<EOS>}]=W_o[\mathrm{<EOS>}]-\mathrm{scale}\left(\hat{G}[\mathrm{<EOS>}]\right) \]

1. Dynamic Gradient Normalization（动态梯度归一化）

解决“怎么稳定而有效地找到 <EOS> 相关的关键梯度维度”；

  • 问题：\(\mathcal{L}^{<EOS>}\) 的梯度在训练初期很大，但会很快变小，导致后期更新力度不足（梯度消失）。
  • 解决：对 <EOS> 的梯度向量 \(\hat{G}[<EOS>]\) 做 动态缩放，保证它的 \(\ell_2\) 范数始终在 \([grad_{\text{low}}, grad_{\text{up}}]\) 区间内。

  • 目的：

    • 防止梯度太小 → 无法有效更新
    • 防止梯度太大 → 更新不稳定
    • 后续：归一化梯度后，取绝对值最大的 前 \(n\) 个维度（top-n）作为关键权重位置，用于后面的 Target Bit Selection（比特翻转目标选择）。

2. Functional Stealthiness via Localized Modification（功能隐蔽性）

解决“怎么在只改 <EOS> 权重的前提下，不破坏其他 token 的输出排序，从而悄悄地影响生成行为”；

  • 方法：只修改输出层 \(W_o\) 中 <EOS> 那一行的部分参数（用 \(\Delta W\) 表示）。

  • 公式：

    • 如果 \(i = <EOS>\)：logit 改成 \((W_o[<EOS>] + \Delta W) \cdot h\)
    • 否则：保持原来的 \(W_o[i] \cdot h\)
    • 效果：
    • 对 <EOS> 的 logit 排名下降（概率降低），减少提前结束生成的可能性
    • 其他 token 的 logit 不变，因此 Softmax 下正常 token 的相对排名完全保留，保证生成的语义和流畅度不受影响

Target Bit Selection

根据选择的 weight，选择翻转的位

优化问题，感觉就是 brute force

\[ b^*=\arg\min_{b\in\{0,...,B-1\}}\left|\mathrm{Fp}(\mathrm{FlipBit}(\boldsymbol{W}_o^i,b))-\boldsymbol{W}_o^{\prime i}\right| \]

image-20250812211926596

文章对比了 progreesive 和 one-shot search

one-shot search is preferred for quantized models due to its speed and comparable effectiveness, while progressive search is more effective for high-precision formats like float16 where bit-level manipulations have finer resolution and stronger cumulative impact

Bit Flipping

使用 Rowhammer 物理攻击，翻转选定的位，但是具体如何翻转不作为该论文的论点

评论