03 | 无约束数值解法 ¶

约 1523 个字 5 张图片预计阅读时间 6 分钟

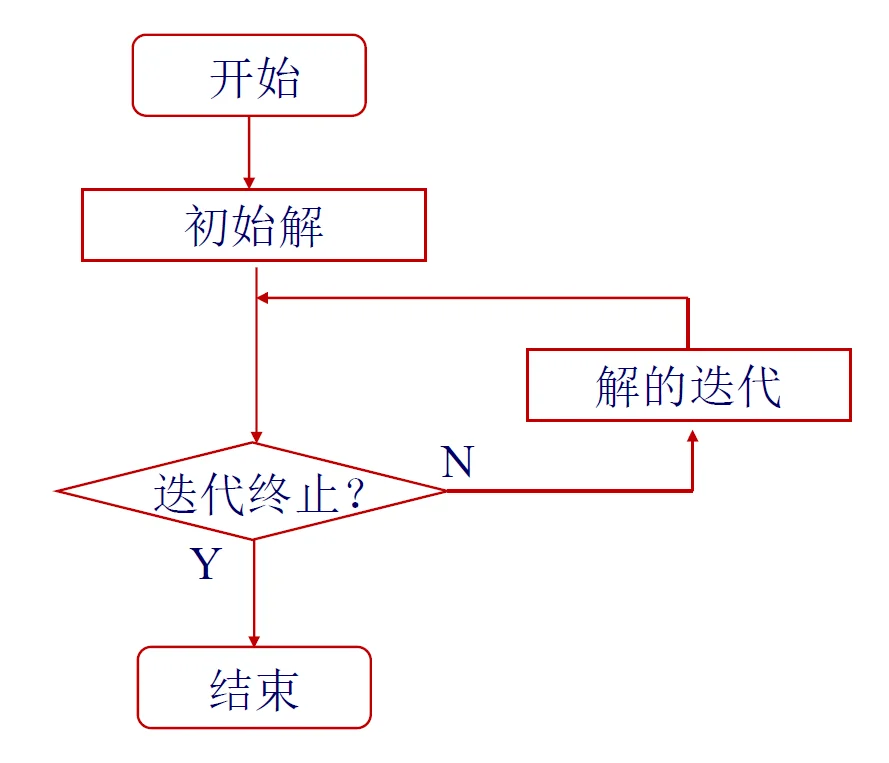
有三个核心的点需要考虑：

迭代方向
步长
终止条件

初始点 ¶

全 0
全随机

迭代方向 ¶

一阶 - GD - 迭代初期 ¶

又叫线搜索法 line search

方向：下降最快的方向是负梯度方向

性质：最优步长的时候 \(\nabla f(x^{k+1}) \perp \nabla f(x^{(k)})\)

优点：计算量小 ( 不需要求 Hessian 矩阵，以及求逆 )，适用于迭代初期

缺点：之字形的迭代路径，接近极值点的时候更严重

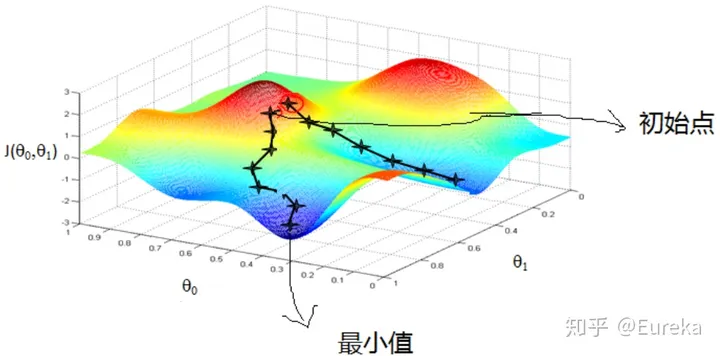
注意

梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

极小值附近的等值面是椭球面

\(X^T \cdot \mathbf{H} \cdot X = c\)

- 如果 \(\mathbf{H}\) 是对角矩阵，则显然是椭圆 - 如果不是的话，相似对角化以后\(X^TM^T \ \Lambda\mathbf{}\ M X = c\)

一阶 - improve GD ¶

problem with GD

Slow at plateaus
get stuck at saddle points

mini-batch SGD¶

批量梯度下降：使用全量样本 \(m\) 进行更新
Stochastic Gradient Descent (SGD) | 随机梯度下降指的是：使用单个样本进行更新
而 mini-batch 就是这两者的折衷，使用一个小批量 \(B< m\) 进行更新

\[ X \in \mathbb{R}^{B \times n}, y \in {1,\dots,K}^{B}\\ \theta := \theta - \frac{\alpha}{B} \sum_{i=1}^{B} \nabla_\theta L(h_\theta(x_i), y_i) \]

如果将小批量的总损失替换为小批量损失的平均值，需要如何更改学习率？

如果将小批量的总损失替换为小批量损失的平均值，则需要将学习率乘以批量大小。

这是因为在计算梯度时，我们使用了小批量中所有样本的信息。因此，如果我们将小批量的总损失替换为小批量损失的平均值，则相当于将每个样本的梯度除以批量大小。因此，我们需要将学习率乘以批量大小，以保持相同的更新步长

Momentum | 动量法¶

公式：

\[ v_t = \gamma v_{t-1} + \eta \nabla_\theta L(\theta) \]

\[ \theta \gets \theta - v_t \]

解释：

\(v_t\) 表示“速度”，\(\gamma\) 是惯性系数（通常 0.9）。
每次更新不仅看当前梯度，还参考之前的更新方向。
优点：减少在陡峭方向的震荡，加速收敛。
类比：小球滚下山，不只是顺着坡度走，还带上惯性，走得更顺畅。

Nesterov Accelerated Gradient (NAG)¶

公式：

\[ v_t = \gamma v_{t-1} + \eta \nabla_\theta L(\theta - \gamma v_{t-1}) \]

\[ \theta \gets \theta - v_t \]

解释：

先用惯性“预估”未来位置 \((\theta - \gamma v_{t-1})\)，再计算梯度。
优点：比普通 Momentum 更快、更精准，避免走过头。
类比：跑步时提前看前方路况，再调整速度和方向。

Adam | Adaptive Moment Estimation¶

公式：

\[ m_t = \beta_1 m_{t-1} + (1-\beta_1) \nabla_\theta L(\theta) \]

\[ v_t = \beta_2 v_{t-1} + (1-\beta_2) (\nabla_\theta L(\theta))^2 \]

\[ \hat{m}_t = \frac{m_t}{1-\beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1-\beta_2^t} \]

\[ \theta \gets \theta - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} \]

解释：
- \(m_t\) 是梯度的一阶矩（均值），\(v_t\) 是二阶矩（方差）。
- 每个参数都有自适应学习率，梯度大时步长小，梯度小步长大。
- 优点：收敛快，几乎适合所有任务。
- 缺点：有时泛化能力不如 SGD。
- 类比：开车时既看前方路坡度（梯度），又调节油门（自适应步长），稳又快。

如果你愿意，我可以帮你画一张 “梯度下降算法收敛路径对比图”，把 SGD / Momentum / NAG / Adam 的公式效果直观地画出来，记忆效果会更好。

你希望我画吗？

二阶 - 牛顿法 - 极值点附近 ¶

思路 ¶

使用泰勒展开

\[ \begin{align*} f(x+\Delta x) \approx f(x) + \nabla f(x)^T \Delta x + \frac{1}{2} \Delta x^T \nabla^2 f(x) \Delta x \end{align*} \]

这里的思想是使用替代函数的方法，我们如果求解出了某个点的梯度和 Hessian 矩阵，那么我们相当于可以得出这个点附近的二次函数 \(g(x)\)，那么我们就可以使用这个二次函数来近似原函数，从而求解出极值点。

对于这个替代函数而言，我们令

\[ \nabla g(\Delta x ) = \nabla f(x) + \nabla^2 f(x) \Delta x = 0 \]

求解这个方程，我们就可以得到极值点的迭代方向

\[ \Delta x = - \nabla^2 f(x)^{-1} \nabla f(x) = - H_k^{-1} \nabla f(x) \]

整理可得

牛顿法迭代公式

\[ x^{(k+1)} = x^{(k)} - H_k^{-1} g_k \]

迭代方向：牛顿方向

\[ p^{(k)}=-H_k^{-1} g_k \]

分析 ¶

优点：多利用了二阶导数的信息，极值点附近收敛速率快。

缺点： - 计算量大，不仅要求Hessian矩阵，还要求Hessian矩阵的逆矩阵； - \(H^{-1}\) 存在数值不稳定的情况（病态） - 远离极值点时，不一定是下降方向，需采用进一步修正（Taylor展开有邻域的限制）

为什么收敛快

至于为什么牛顿法收敛更快，通俗来说梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。

改进思路：不直接求逆

我们只需要得到 \(\nabla^2 f(x) \Delta x = - \nabla f(x)\) 的解，而不需要求逆矩阵；而这个问题的形式其实就是求解 \(Ax = b\) 这个矩阵方程的解，可以使用梯度下降等方法求近似解

二阶 - 修正牛顿法 - 解决数值稳定性问题 ¶

Levenberg-Marquardt 修正

因为 \(H^{-1}\) 存在数值不稳定的情况（病态），所以我们可以使用一个正则化项来保证 \(H^{-1}\) 的稳定性 , 变为正定矩阵 , 保证 \(p\) 是下降方向

求解方程

\[ \begin{align*} (\nabla^2 f(x)+\mu I) &\Delta x = - \nabla f(x)\\ &\Delta x = - (\nabla^2 f(x)+\mu I)^{-1} \nabla f(x) \end{align*} \]

其中 \(\mu\) 是一个正则化参数，用于控制 \(H^{-1}\) 的稳定性

\(\mu_{k} > \left|\lambda_{\text{min}}\right|\) 其中，\(\lambda_{\text{min}}\) 为 \(\nabla^2 f\left(x_k\right)\) 的最小负特征值
如果不求特征值，可以从较小的 \(\mu\) 值试探
- \(\mu \rightarrow 0\) : 牛顿法
- \(\mu \rightarrow \infty\) : 最速下降法

二阶 - 拟牛顿法 ¶

在牛顿法的迭代中，需要计算海森矩阵的逆矩阵 \(\boldsymbol{H}^{-1}\) ，这一计算比较复杂，考虑用一个 \(n\) 阶矩阵 \(\boldsymbol{G}_{k}=\boldsymbol{G}\left(x^{(k)}\right)\) 来近似代替 \(\boldsymbol{H}_{k}^{-1}=\boldsymbol{H}^{-1}\left(x^{(k)}\right)\) 。这就是拟牛顿法的基本想法。

要找到近似的替代矩阵，必定要和 \(\boldsymbol{H}_{k}\) 有类似的性质。先看下牛顿法迭代中海森矩阵 \(\boldsymbol{H}_{k}\) 满足的条件。首先 \(\boldsymbol{H}_{k}\) 满足以下关系：

在 \(x^{k+1}\) 处进行展开

\[ \nabla f(x)=g_{k+1}+\boldsymbol{H}_{k+1}\left(x-x^{(k+1)}\right) \]

将 \(\boldsymbol{x}=\boldsymbol{x}^{k}\) 代入

\[ g_{k}-g_{k+1}=\boldsymbol{H}_{k+1}\left(x^{(k)}-x^{(k+1)}\right) \]

记 \(y_{k}=g_{k+1}-g_{k}, \delta_{k}=x^{(k+1)}-x^{k}\) ，则

\[ \begin{aligned} y_{k} & =\boldsymbol{H}_{k+1} \delta_{k} \\ \delta_{k}& = \boldsymbol{H}_{k+1}^{-1} y_{k} \quad 拟牛顿条件(Secant\ equation) \end{aligned} \]

其次，如果 \(H_k\) 是正定的（\(H_k^{-1}\) 也是正定的），那么保证牛顿法的搜索方向 \(p_k\) 是下降方向。这是因为搜索方向是 \(p_k = -H_k^{-1}g_k\)。

由

\[ x^{(k+1)} = x^{(k)} - H_k^{-1}g_k \]

有

\[ x = x^{(k)} - \lambda H_k^{-1}g_k = x^{(k)} + \lambda p_k \]

则 \(f(x)\) 在 \(x^{(k)}\) 的泰勒展开可近似为

\[ \begin{align} f(x) = f\left(x^{(k)}\right) - \lambda g_k^T H_k^{-1} g_k \end{align} \]

由于 \(H_k^{-1}\) 正定，故 \(g_k^T H_k^{-1} g_k > 0\)。当 \(\lambda\) 为一个充分小的正数时，有 \(f(x) < f\left(x^{(k)}\right)\)，即搜索方向 \(p_k\) 是下降方向。

因此拟牛顿法将 \(G_k\) 作为 \(H_k^{-1}\) 近似。要求 \(G_k\) 满足同样的条件下，首先，每次迭代矩阵 \(G_k\) 是正定时，\(G_k\) 满足下面的拟牛顿条件：

\[ \begin{align} G_{k+1} y_k = \delta_k \end{align} \]

按照拟牛顿条件，在每次迭代中可以选择更新矩阵 \(G_{k+1}\)：

\[ \begin{align} G_{k+1} = G_k + \Delta G_k \end{align} \]

DFP 算法 ¶

在 DFP（Davidon-Fletcher-Powell）算法中，我们选择 \(G_k\) 作为 \(H_k^{-1}\) 的近似。假设在每次迭代中，矩阵 \(G_{k+1}\) 由 \(G_k\) 加上两个附加项构成：

\[ G_{k+1} = G_k + P_k + Q_k \]

其中，\(P_k\) 和 \(Q_k\) 是待定矩阵。那么，

\[ G_{k+1}y_k = G_k y_k + P_k y_k + Q_k y_k \]

为了使 \(G_{k+1}\) 满足拟牛顿条件，我们希望 \(P_k\) 和 \(Q_k\) 满足以下条件：

\[ \begin{aligned} &P_k y_k = \delta_k \\ &Q_k y_k = -G_k y_k \end{aligned} \]

因此，我们可以这样选择：

\[ \begin{aligned} &P_k = \frac{\delta_k \delta_k^T}{\delta_k^T y_k} \\ &Q_k = -\frac{\delta_k y_k^T G_k}{y_k^T G_k y_k} \end{aligned} \]

这将导致矩阵 \(G_{k+1}\) 的迭代公式为：

\[ G_{k+1} = G_k + \frac{\delta_k \delta_k^T}{\delta_k^T y_k} - \frac{\delta_k y_k^T G_k}{y_k^T G_k y_k} \]

如果初始矩阵 \(G_0\) 是正定的，那么可以证明在迭代过程中每个矩阵 \(G_k\) 也都是正定的。

可以证明 :

当目标函数为严格凸二次函数时 , 可经有限步迭代收敛于极值（二次终止性）。为什么不是 1 步 ?

共轭梯度法 ¶

参考文献：共轭梯度法的简单直观理解 -CSDN 博客

在这里插入图片描述

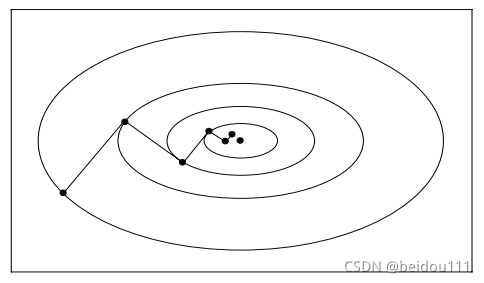
为什么会走出这一 Z 形线呢？因为梯度下降的方向恰好与 f 垂直，也就是说和等高线垂直。沿着垂直于等高线的方向，一定能让函数减小，也就是最快地下了一个台阶。但是最快下台阶并不意味着最快到达目标位置（即最优解），因为你最终的目标并不是直对着台阶的。

为了修正这一路线，采用另一个方向：即共轭向量的方向。

对照梯度下降法，每次向下走的方向不是梯度了，而是专门的一个方向 \(\vec{d}\) 除此之外和梯度下降法几乎一样。

共轭向量 \(p_i^T A p_j = 0\), 其中 A 是一个对称正定矩阵。\(p_i,p_j\) 是一对共轭的向量。

可见，共轭是正交的推广化，因为向量正交的定义为：\(p_i^T\cdot p_j = 0\)

共轭比正交中间只多了个矩阵 A，而矩阵的几何意义正是对一个向量进行线性变换（可见 Gilber Strang 的线代公开课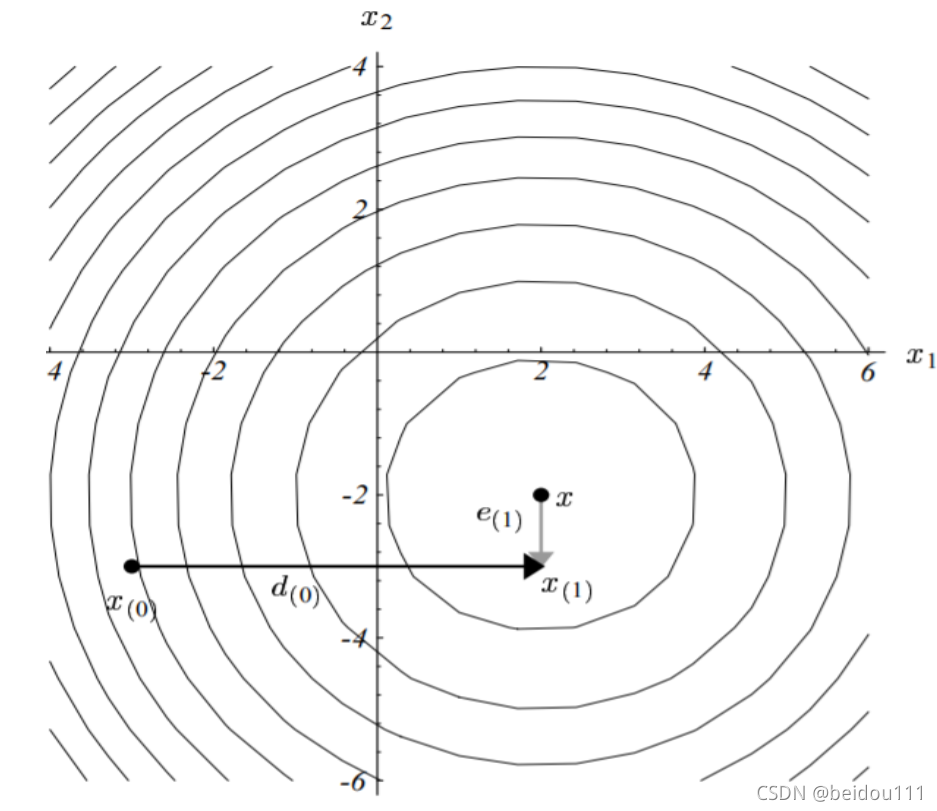）。因此共轭向量的意思就是一个向量经过线性变换（缩放剪切和旋转）之后与另一个向量正交。在这里插入图片描述

步长选择 - determine convergence ¶

精准法 ¶

设计思想：沿搜索方向的目标函数值最小

\[ \lambda_{k}=\arg \min \limits_{\lambda} f\left(x_k+\lambda p_k\right) \]

但是求解上边的优化问题代价比较大

Armijo 准则 ¶

选取 \(\sigma \in (0,1)\)

\[ f(x_k + \lambda p_k) \leq f(x_k) + \sigma \lambda \nabla f_k^T p_k \]

回退法 ¶

backtracking line search

Goldstein 准则 ¶

找一个步长点上下限

\(\sigma \in (0,\frac{1}{2})\)

\[ \begin{cases} f(x_k + \lambda p_k) \leq f(x_k) + \sigma \lambda \nabla f_k^T p_k\\ f(x_k + \lambda p_k) \geq f(x_k) + (1-\sigma) \lambda \nabla f_k^T p_k \end{cases} \]

固定步长 ¶

不一定能收敛

\[ \lambda_k = \lambda \]

Diminishing rule¶

\[ \lambda = \frac{1}{\sqrt{k+1}} \]

一定能保证收敛，只不过可能慢一点，用于测试模型的性能

迭代终止准则 Terminate ¶

前后差值够小 ¶

绝对误差准则

\[ \|x_{k+1} - x_k\| \leq \varepsilon_1 \quad |f(x_{k+1}) - f(x_k)| \leq \varepsilon_2 \]

相对误差准则

\[ \frac{\|x_{k+1} - x_k\|}{\|x_k\|} \leq \varepsilon_3 \quad \frac{|f(x_{k+1}) - f(x_k)|}{|f(x_k)|} \leq \varepsilon_4 \]

梯度够小 ¶

\[ \left\|\nabla f_k\right\| \leq \epsilon \]

完整算法案例 ¶

梯度下降算法

输入：目标函数 \(f(x)\) ，梯度函数 \(g(x)=\nabla f(x)\) ，计算精度 \(\varepsilon\)
输出： \(f(x)\) 的极小点 \(x^*\)
步骤：
1. 选取初值 \(x^{(0)}\)，令 \(k=0\)
2. 计算函数值 \(f(x^{(k)})\)
3. 计算梯度 \(\nabla f(x^{(k)})\)
  - 若 \(\|\nabla f(x^{(k)})\| < \varepsilon\)，停止迭代，输出 \(x^* = x^{(k)}\)
  - 否则，
    - 搜索方向：负梯度 \(p_k = -\nabla f(x^{(k)})\)
    - 求步长 \(\lambda_k\) 使得 :\(f(x^{(k)} + \lambda_k p_k) = \min_{\lambda \geq 0} f(x^{(k)} + \lambda p_k)\)
4. 更新： \(x^{(k+1)} = x^{(k)} - \lambda_k \nabla f(x^{(k)})\)
5. 若满足终止条件 :
  - \(|f(x^{(k+1)}) - f(x^{(k)})| < \varepsilon\) 或
  - \(\|x^{(k+1)} - x^{(k)}\| < \varepsilon\) 则停止迭代，输出 \(x^* = x^{(k+1)}\)
6. 否则 \(k = k+1\)，返回步骤 3

03 | 无约束 数值解法 ¶