01 | 基本概念 ¶

约 2532 个字 1 张图片预计阅读时间 10 分钟

基本定义 ¶

参考视频

随机过程 ¶

{ $X(t);t\in T$ } 在 $T$ 中取任一 $t$ 的随机变量集合。

股票 243 个交易日的价格走向

样本函数 ¶

$X(t)$ ，为 $t$ 的函数。（所有随机变量取到可能出现的值）

股票一天的走势；三角函数振幅给定

状态：给定 $t_0$ ，$X(t_0)$ 的与随机变量相关的值。
状态空间：所有状态取值构成的集合。

数字特征 ¶

大部分随机过程的数字特征都是在和求期望打交道

方差是用来度量单个随机变量的离散程度
协方差则一般用来刻画两个随机变量的相似程度（相关性）

如何理解协方差

如何直观地理解「协方差矩阵」？ - 知乎

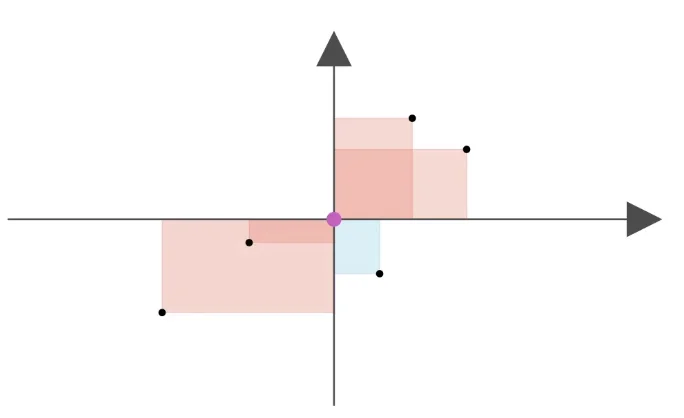
协方差：用与均值面积正负来刻画相关性 ( 一三象限是正相关，二四象限是负相关 )

把原点看作 $(\bar{x},\bar{y})$，那么 $\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})$ 就可以理解为这些矩形的面积了

图片出自如何通俗地解释协方差｜马同学图解数学 _ 哔哩哔哩 _bilibili

单个随机过程 ¶

均值函数 $\mu(t) = E\big(X(t)\big)$
方差函数 $\sigma^2(t) = E\big(X^{2}(t)\big) - \mu^{2}(t) = C(t,t)$
协方差函数 $C(s,t) = E\big(X(s)X(t)\big) - \mu(s)\mu(t)$
相关函数 $R(s,t) = E\big(X(s)X(t)\big)$, 是协方差函数的第一项

理解自相关的例子：家族男性当中：父子身高的相关性、爷孙身高的相关性
自协方差：$t$和$t+\tau$的信号幅值变化相同，想找一个函数来去掉直流分量的影响

$\text{Var}(A+B) = \text{Var}(A) + \text{Var}(B) + 2\text{Cov}(A, B)$
$\text{Var}(A) = \text{Cov}(A, A)$
$\text{Cov}(A, B) = E(AB) - E(A)E(B)$
$\text{Var}(A) = E(A^2) - [E(A)]^2$

两个随机过程 ¶

互协方差函数 $C_{XY}(s,t) = E\big(X(s)Y(t)\big) - \mu(s)\mu(t)$
互相关函数 $R_{XY}(s,t) = E\big(X(s)Y(t)\big)$

自己和别人的两个时刻的对比平稳随机过程的自相关和互相关（函数/系数）的性质 - 知乎

二阶矩过程的均值、自相关、自协方差都存在

正态过程 ¶

$\{X(t),t\in T\}$ 是一随机过程，对任意整数 $n\geq1$ 及

任意 $t_1,t_2,\cdotp\cdotp\cdotp t_n\in T,(X(t_1),X(t_2),\cdotp\cdotp\cdotp X(t_n))$ 服从 $n$ 维正态分布，则称 $\{X(t),t\in T\}$ 是正态过程。

正态过程的全部统计特性完全由它的均值函数和自协方差函数所确定。

如果对任意的 $t_1,t_2\in T$, 恒有 $C_XY(t_1,t_2)=0$ 称随机过程 $\left\{X(t)\right\}$ 和 $\left\{Y(t)\right\}$ 是不相关的。

题型 ¶

样本函数 ¶

设 $X(t) = A + Bt$, $t \geq 0$。这里随机变量 $A$ 和 $B$ 服从相同的 0-1 分布，$P(A = 1) = p \in (0, 1)$。若 $E[A(B - 1)] = 0$。则该过程的所有样本函数

选项：

A. 有两条，且分别为 $x_1(t) = 1 + t$, $x_2(t) = 0$。

B. 有四条，且分别为 $x_1(t) = 1 + t$, $x_2(t) = 0$, $x_3(t) = t$, $x_4(t) = 1$。

C. 有三条，且分别为 $x_1(t) = 1 + t$, $x_2(t) = 0$, $x_3(t) = t$。

D. 有三条，且分别为 $x_1(t) = 1 + t$, $x_2(t) = 0$, $x_3(t) = 1$。

答案：A

通过条件 $E[A(B - 1)] = 0$，可以知道 A 和 B 并不独立

求数字特征 ¶

需要搞清楚谁是随机变量

例题

3. 下列式子中的各记号同教材或课件，则等式成立的是 ()

\[ \begin{aligned}&(A)C_{XY}(s,t)=C_{YX}(s,t)\\ &(B)D_{X}(t)=C_{X}(t,t)\\ &(C)\mu_{X}(s)+\mu_{X}(t)=\mu_{X}(s+t)\\ &(D)R_{X}(s,t)=\mu_{X}(s)\mu_{X}(t)\end{aligned} \]

那为什么有时候说 $C_{XY}(s, t) \neq C_{YX}(s, t)$？

这是因为在随机过程中，$C_{XY}(s, t)$ 的两个维度含义不同：

$C_{XY}(s, t) = \mathrm{Cov}(X(s), Y(t))$
$C_{YX}(s, t) = \mathrm{Cov}(Y(s), X(t))$

你可以看到这两个表达式不是简单地交换了变量，而是交换了变量和时间索引的位置。

设随机过程 $X(t)=At+B$ ，其中 $A$、$B$ 独立同分布，$P(A=1)=0.6$ ，$P(A=-1)=0.4$ 。

(1) $X(t)$ 的所有样本函数为 $X(t)=t+1$ ；$X(t)=-t+1$ ；$X(t)=t-1$ ；$X(t)=-t-1$

(2) $X(1)=A+B$ 的分布律为 $P[X(1)=0]=0.48$ ； $P[X(1)=2]=0.36$ ；$P[X(1)=-2]=0.16$

(3) { $X(t);t∈T$ } 的均值函数为 $E[X(t)]=tE(A)+E(B)=0.2t+0.2$

(4) 自相关函数为

\[ \begin{aligned} R_X(t_1,t_2)&=E[X(t_1)X(t_2)]=E[(At_1+B)(At_2+B)]\\ &=t_1t_2E(A^2)+(t_1+t_2)E(AB)+E(B^2)=t_1t_2+0.04(t_1+t_2)+1 \end{aligned} \]

（求 $E^2(A)$ 应该直接带定义，比用方差和均值求方便一点）

随机相位正弦波 $X(t) = \alpha \cos(\beta t + \theta)$，$-\infty < t < +\infty$, 其中，$\alpha, \beta$ 为常数，$\theta$ 是在 $[0, 2\pi]$ 上均匀分布的随机变量，求 $X(t)$ 的均值函数、方差函数、相关函数、协方差函数

解：

$\theta$ 的概率密度为

$f(\theta) = \begin{cases} \frac{1}{2\pi}, & 0 \leq \theta \leq 2\pi \\ 0, & \text{其他} \end{cases}$

均值函数为：

\[ E(X(t)) = \int_{-\infty}^{+\infty} X(t) f(\theta) \, \mathrm{d}\theta = \int_{0}^{2\pi} \alpha \cos(\beta t + \theta) \frac{1}{2\pi} \, \mathrm{d}\theta = 0 \]

\[ \begin{align*} R(s, t) &= E(X(s) X(t)) = \int_{-\infty}^{+\infty} X(t) X(s) f(\theta) \, \mathrm{d}\theta\\ &= \int_{0}^{2\pi} \alpha^2 \cos(\beta t + \theta) \cos(\beta s + \theta) \frac{1}{2\pi} \, \mathrm{d}\theta \quad \rightarrow \text{积化和差}\\ &=\frac{\alpha^{2}}{2\pi}\frac{1}{2}\int_{0}^{2\pi}\cos\beta(t-s)+\cos(\beta(t+s)+2\theta)\mathrm{d}\theta\\ &=\frac{\alpha^{2}}{2}\cos\beta(t-s)\\ C(s,t)&=E\left(X(s)X(t)\right)-m(s)m(t)=R(s,t)\\ D(t)&=C(t,t)=\frac{\alpha^{2}}{2} \end{align*} \]

设随机过程 $X(t)=V\cdot t$, 其中 $V$ 是在 (0,1) 上服从均匀分布的随机变量

求过程 $X(t)$ 的均值和自相关函数

解：

已知随机变量 $V$ 的概率密度为：

$f(v)=\begin{cases}1,v\in(0,1)\\0,\text{其他}\end{cases}$

\[ \begin{aligned} &E\big(X(t)\big)=\int_{-\infty}^{+\infty}x(t)f(v)\:\mathrm{d}v=\int_{0}^{1}vt\:\mathrm{d}v=\frac{t}{2}\\ &R_{X}(t_{1},t_{2})=E\big(X(t_{1})Y(t_{2})\big)=E(Vt_{1}Vt_{2})=\int_{0}^{1}v^{2}t_{1}t_{2}\:\mathrm{d}v=\frac{t_{1}t_{2}}{3} \end{aligned} \]

设两个连续时间的随机相位信号 ,$X(t)=\sin(w_{0}t+\Phi)$,$Y(t)=\cos(w_{0}t+\Phi)$, 其中 $w_0$ 为常数，$\Phi$ 在 $(-\pi,\pi)$ 上服从均匀分布，求互协方差函数。

解：首先求两个信号的均值：

$E(X(t))=E(\sin(w_{0}t+\Phi))=\int_{-\pi}^{\pi}\sin(w_{0}t+\Phi)\frac{1}{2\pi}\mathrm{d}\varphi=0$

$E(Y(t))=E(\cos(w_{0}t+\Phi))=\int_{-\pi}^{n}\cos(w_{0}t+\Phi)\frac{1}{2\pi}\mathrm{d}\varphi=0$

互协方差函数为：

\[ C_{XY}(t_{1},t_{2})=R_{XY}(t_{1},t_{2})-E(X(t_{1}))E(Y(t_{2}))=R_{XY}(t_{1},t_{2}) \]

其中：

\[ \begin{aligned} R_{XY}(t_{1},t_{2})&=E(X(t_{1})Y(t_{2}))=E(\sin(w_{0}t_{1}+\Phi)\cos(w_{0}t_{2}+\Phi))\\ &=\int_{-\pi}^{\pi}\sin(w_{0}t_{1}+\Phi)\cos(w_{0}t_{2}+\Phi)\frac{1}{2\pi}\mathrm{d}\varphi\\ &=\frac{1}{4\pi}\int_{-\pi}^{\pi}\sin(w_{0}(t_{2}-t_{1}))+\sin(w_{0}(t_{1}+t_{2})+2\Phi)\mathrm{d}\varphi\\ &=\frac{1}{2}\sin(w_{0}(t_{2}-t_{1}))+\frac{1}{4\pi}\int_{-\pi}^{\pi}\sin(w_{0}(t_{1}+t_{2})+2\Phi)\mathrm{d}\varphi\\ &=\frac{1}{2}\sin(w_{0}(t_{2}-t_{1})) \end{aligned} \]

导函数的数字特征

⚠️这个题目不在考试范围内，也不是老师讲过的内容，是在 b 站视频里面看到的题目

设随机过程 $X(t)$ 的均值与自相关函数为 $m_{X}= 5\sin t$ , $R_{X}( t, s) = 3\mathrm{e} ^{- 0. 5( s- t) ^{2}}$ 试求$Y(t)=X^\prime(t)$的均值和自相关函数

\[ \begin{aligned}&E\big(Y(t)\big)=\frac{\mathrm{d}}{\mathrm{d}t}E\big(X(t)\big)=5\cos t\\&R_{Y}(t,s)=\frac{\partial^2}{\partial s\:\partial t}R_X(t,s)\end{aligned} \]

例题

随机过 $X(t)=A\cos wt,Y(t)=(1-B)\cos wt$, 其中 $A,B$ 同为均值为 2，方差为 $\sigma^2$ 的高斯随机变量，$A,B$ 统计独立，$w$ 为非零常数。求两个随机过程的均值、互相关函数、互协方差函数

\[ \begin{aligned} &E\big(X(t)\big)=E(A\cos wt)=2\cos wt\\ &E\big(Y(t)\big)=E\big((1-B)\cos wt\big)=-\cos wt\\ &R_{XY}(t_{1},t_{2})=E\big(X(t_{1})Y(t_{2})\big)=E\big(A\cos wt_{1}\times(1-B)\cos wt_{2}\big)=-2\cos wt_{1}\cos wt_{2}\\&C_{XY}(t_{1},t_{2})=R_{XY}(t_{1},t_{2})-E\big(X(t)\big)E\big(Y(t)\big)=0 \end{aligned} \]

例题

设 $X(t) = At^B$，其中 $A \sim N(1,1)$，$P(B=1) = P(B=2) = 0.5$，$A$ 和 $B$ 相互独立。计算：

(1) 随机过程 $\{X(t); t \geq 0\}$ 的均值函数和自相关函数；

(2) $P(X(2) < 4)$；

(3) $P(X(1) > 1, X(2) < 4)$。

答案：

(1) 均值函数和自相关函数：

\[ \mu_X(t) = \frac{t + t^2}{2} \]

\[ R_X(s, t) = ts + t^2s^2 \]

(2) $$ P(X(2) < 4) = P(B=1)P(A < 2) + P(B=2)P(A < 1) = 0.67 $$

(3) $$ P(X(1) > 1, X(2) < 4) = P(B=1)P(1 < A < 2) + P(B=2)P(A > 1, A < 1) = 0.17 $$

例题

设 $X(t) = A\cos t + B\sin t,\ t \geq 0$，其中 $A \sim N(1, 2),\ B \sim N(0, 2)$，且 $A, B$ 独立。

求：

自相关函数 $R_X(s,t)$
$X\left(\dfrac{3\pi}{4}\right)$ 的分布

答案：

自相关函数：

\[ R_X(s,t) = 3\cos s \cos t + 2\sin s \sin t \]

分布：

\[ X\left(\dfrac{3\pi}{4}\right) \sim N\left(-\dfrac{\sqrt{2}}{2},\ 2\right) \]

求分布函数 ¶

通过投掷一个硬币定义一个随机过程 :$X(t)=\begin{cases} \cos\pi t, 出现正面 \\ 2t, 出现反面 \end{cases}$(1) $F\left(\frac{1}{2},x\right), F(1,x)$(2) $F\left(\frac{1}{2},1,x,y\right)$

解 :

(1)(2)

$F\left(\frac{1}{2},x\right)$ 相当于是求 $X\left(\frac{1}{2}\right)$ 的分布函数，这里要注意 $X\left(\frac{1}{2}\right)$ 已经是一个随机变量

$X\left(\frac{1}{2}\right)=\begin{cases} \cos\frac{\pi}{2}, 出现正面 \\ 1, 出现反面 \end{cases}$

$X\left(\frac{1}{2}\right)$	0	1
	$\frac{1}{2}$	$\frac{1}{2}$

$F\left(\frac{1}{2},x\right)=P\left\{X\left(\frac{1}{2}\right)<x\right\}=\begin{cases} 0, -\infty < x \leq 0 \\ \frac{1}{2}, 0 < x \leq 1 \\ 1, 1 < x < +\infty \end{cases}$

$F\left(\frac{1}{2},1,x,y\right)=P\left\{X\left(\frac{1}{2}\right)<x,X(1)<y\right\}$

先求 $X(\frac{1}{2}), X(1)$ 的联合分布律 :

$X(\frac{1}{2})$	$X(1) = -1$	$X(1) = 2$
$0$	$\frac{1}{4}$	$\frac{1}{4}$
$1$	$\frac{1}{4}$	$\frac{1}{4}$

设 $X(t)=At+B,t≥0$，这里 $A$ 和 $B$ 相互独立服从相同分布，$P(A=1)=0.6$，$P(A=-1)=0.4$

(1) 写出 $X(t)$ 的全部样本函数；

(2) 求 $(X(1),X(2))$ 的联合分布律及 $X(2)$ 的边际分布律；

(3) 求 $\{X(t);t≥0\}$ 的均值函数和自相关函数。

答案

5 (1) - $x_{1}(t)=t+1$ - $x_{2}(t)=t-1$ - $x_{3}(t)=-t+1$ - $x_{4}(t)=-t-1$。

(2)

$X(1)$ $\backslash$ $X(2)$	-3	-1	1	3
-2	0.16	0	0	0
0	0	0.24	0.24	0
2	0	0	0	0.36
$P(X(2)=j)$	0.16	0.24	0.24	0.36

(3) - $E[X(t)]=EAt+EB=0.2t+0.2$ - $E[X(t)X(s)]=EA^{2}ts+E(AB)(s+t)+E(B^{2})=ts+0.04(t+s)+1$。

正态过程相关 ¶

下列关于随机过程的叙述正确的有

A. 二阶矩过程的自相关函数一定不小于自协方差函数。

B. 二阶矩过程的均值函数一定存在。

C. 对于随机过程 $\{X(t); -\infty<t<\infty\}$ 中给定的 $t$，$X(t)$ 是随机变量。

D. 若对任意 $t\in(-\infty,\infty)$，$X(t)$ 服从正态分布，则 $\{X(t); -\infty<t<\infty\}$ 是正态过程。

A. 二阶矩没有什么限制，虽然自协方差需要减两个均值，但是均值不一定是正数，这一点需要格外注意

D. 若随机过程 ${X(t),\ t \in T}$ 中，任取有限个时刻 $t_1, t_2, \cdots, t_n$，对应的随机向量 $(X(t_1), X(t_2), \cdots, X(t_n))$ 服从多元正态分布，则称其为正态过程。

需要联合分布也服从正态

设 {$X(t);t\geq0$} 是正态过程，$EX(t)=0$，$E\left[X(t)X(s)\right]=1+ts+0.5(t+s)$

则 $X(1)$ 服从 __ 分布，$X(0)+X(1)$ 服从 __ 分布，$X(1)$ 与 $X(-1)$ 独立吗？并说明理由 __ 。

答案 - N(0,3)，N(0,7)，是，因为它们是二元联合正态分布且协方差为0。

解析 📌 求 $X(0) + X(1)$ 的分布

$\mathbb{E}[X(0) + X(1)] = 0 + 0 = 0$
协方差函数和自相关函数是一样的，因为均值是 0
方差：$\mathrm{Var}(X(0) + X(1)) = \mathrm{Var}(X(0)) + \mathrm{Var}(X(1)) + 2\mathrm{Cov}(X(0), X(1))= 1 + 3 + 2(1.5) = 4 + 3 = 7$

📌 问题：$X(1)$ 与 $X(-1)$ 独立吗？

先注意：题目最初只说 $t \geq 0$，但这里又问了 $X(-1)$，我们暂时延拓过程到实数轴上，继续看协方差：

\[ \mathrm{Cov}(X(1), X(-1)) = R_X(1, -1) = 1 - 1 + 0 = 0 \]

又因为 $X(t)$ 是高斯过程（正态过程），而高斯过程中零协方差 ⇒ 独立性（只在联合正态情形成立）

设 $\{X(t); t \geq 0\}$ 是正态过程，$E[X(t)] = 2t$，$Cov(X(t), X(s)) = ts + 4$

(1) $X(t)$ 服从 $\underline{\qquad\qquad\qquad\qquad}$ 分布。

(2) $X(t) - X(s)$ 服从 $\underline{\qquad\qquad\qquad\qquad}$ 分布。

(3) $Cov(X(t+1) - X(t),\ X(s+1) - X(s)) = \underline{\qquad}$。

(4) 令 $Y(t) = X(t+1) - X(t)$，随机过程 $\{Y(t); t \geq 0\}$ 是宽平稳过程吗？为什么？$\underline{\qquad\qquad\qquad\qquad}$

答案与推导

(1) $X(t)$ 服从 $N(2t,\, 4 + t^2)$

均值 $E[X(t)] = 2t$
方差 $Cov(X(t), X(t)) = t^2 + 4$

(2) $X(t) - X(s)$ 服从 $N(2(t-s),\, (t-s)^2)$

均值 $E[X(t) - X(s)] = 2t - 2s = 2(t-s)$
方差：

\[ \begin{aligned} Var(X(t) - X(s)) &= Cov(X(t)-X(s), X(t)-X(s)) \\ &= Var(X(t)) + Var(X(s)) - 2Cov(X(t), X(s)) \\ &= (t^2+4) + (s^2+4) - 2(ts+4) \\ &= (t-s)^2 \end{aligned} \]

(3) $Cov(X(t+1) - X(t),\ X(s+1) - X(s)) = 1$

计算：

\[ \begin{aligned} &Cov(X(t+1)-X(t),\ X(s+1)-X(s)) \\ &= Cov(X(t+1), X(s+1)) - Cov(X(t+1), X(s)) - Cov(X(t), X(s+1)) + Cov(X(t), X(s)) \\ &= (t+1)(s+1)+4 - (t+1)s+4 - t(s+1)+4 + ts+4 \\ &= 1 \end{aligned} \]

(4) 是，因为 $Y(t)$ 首先因为$X(t)$是正态过程，线性组合仍然是二阶矩过程

均值 $\mu_t = 2$ 是常数
协方差 $C_Y(t, t+\tau) = 1$
自相关函数 $R_Y(t,t+\tau) = C_Y(t,t+\tau) +\mu_t\mu_{t+\tau} = 1+2\times2 = 5$

与 $t$ 无关，满足宽平稳过程的定义。

\(X(\frac{1}{2})\)	\(X(1) = -1\)	\(X(1) = 2\)
\(0\)	\(\frac{1}{4}\)	\(\frac{1}{4}\)
\(1\)	\(\frac{1}{4}\)	\(\frac{1}{4}\)

01 | 基本概念 ¶

基本定义 ¶

随机过程 ¶

样本函数 ¶

数字特征 ¶

单个随机过程 ¶

两个随机过程 ¶

正态过程 ¶

题型 ¶

样本函数 ¶

求数字特征 ¶

求分布函数 ¶

正态过程相关 ¶

习题 ¶