跳转至

06 | Infer Optimization

约 1066 个字 4 行代码 16 张图片 预计阅读时间 4 分钟

正在施工中👷..

Key-value cache

  • Key-value cache

原理

在 Decoder 阶段，使用 Auto Regressive 机制

\[ Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V \]

由于有 Mask 机制，每次有新的 token 加入的时候，只需要做 \(Q_{new}\) 和 \(K_{old}\) 的注意力计算，而不用重新计算整个序列。

所以，我们只需要保存 \(K_{old}\) 和 \(V_{old}\) ( 因为只用到了 KV)，就可以实现高效的增量生成。

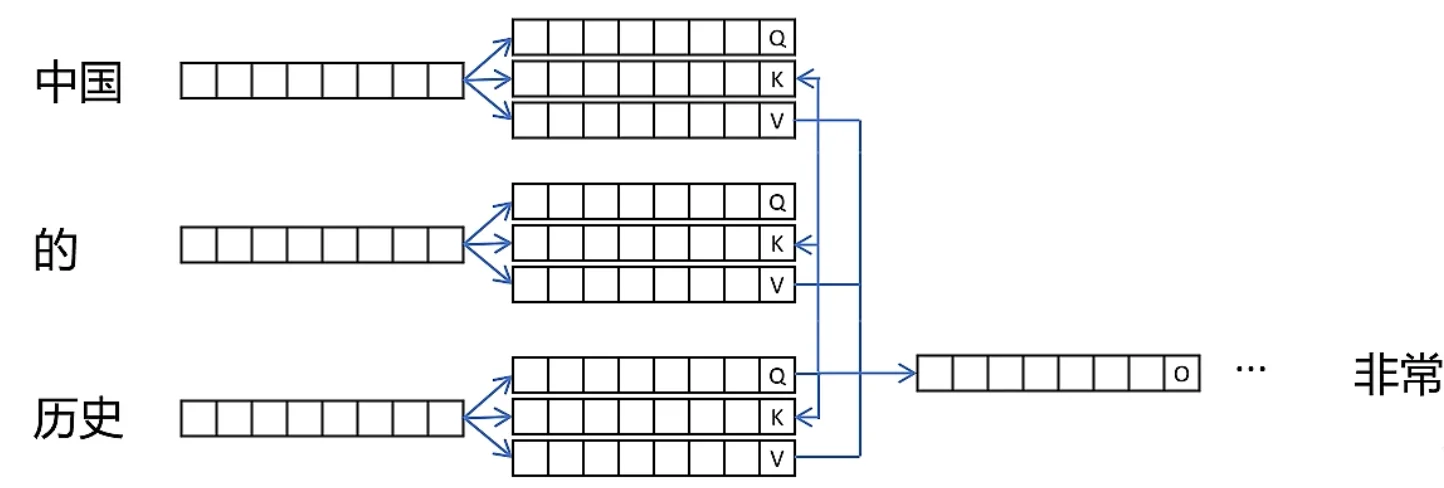
image-20250812230838959

值得注意的是，KV 缓存的大小通常和模型本身大小是同一级别，也是一种空间换时间的策略

pie
    title Memory Usage of 13B LLM on A100-40GB
    "Parameters" : 65
    "KV Cache" : 30
    "Others" : 5

Paged Attention

为什么需要

操作系统

操作系统需要给进程预先分配内存吗

每个页 4K

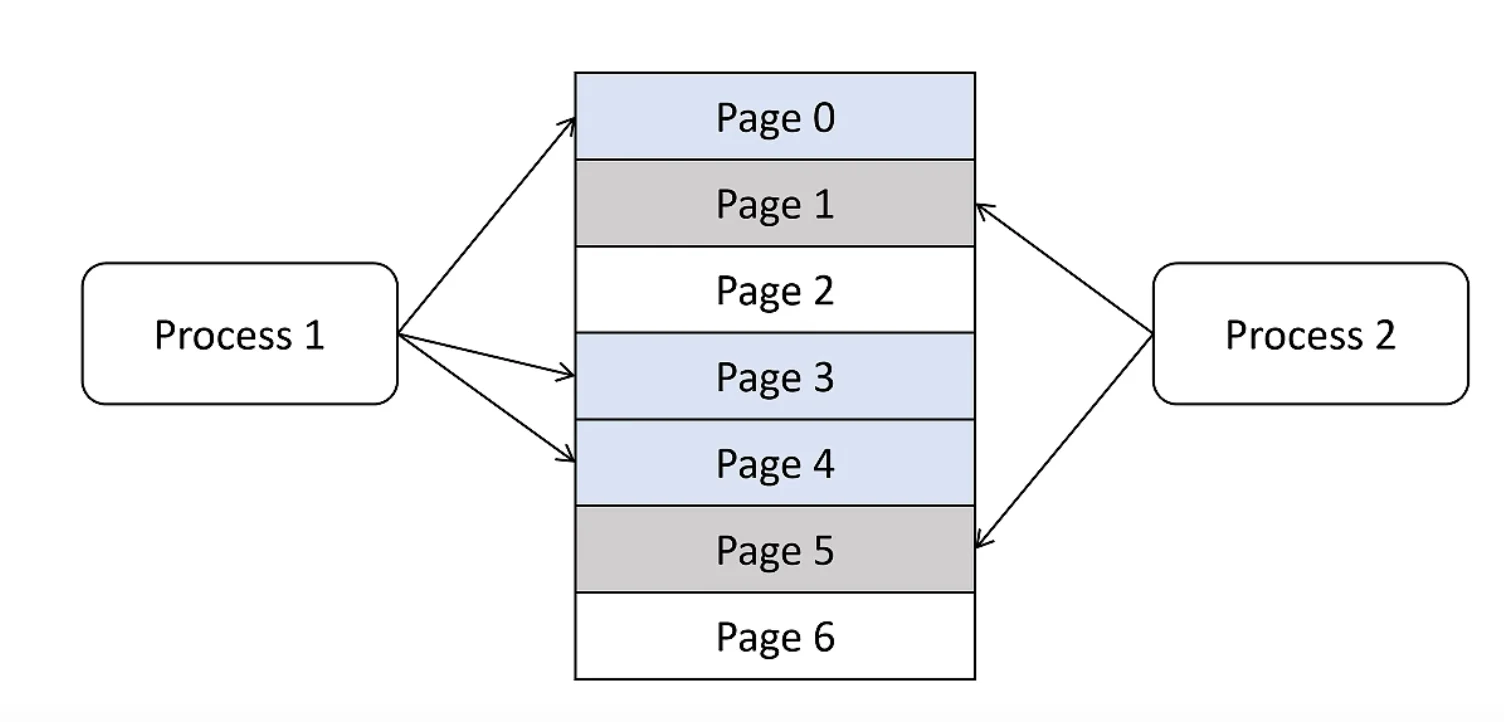
image-20250813000031813

原理

  • 不预分配，按需调用
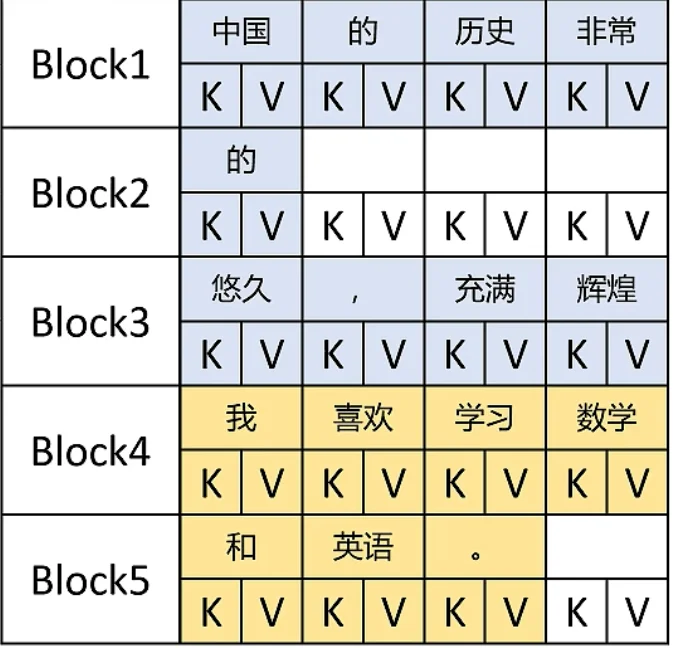
  • 按块 Block 分配内存，碎片更小 image-20250813000142399
  • 虚拟内存：逻辑内存是连续的，通过映射表链接到物理内存（实际分配不连续）；方便调用

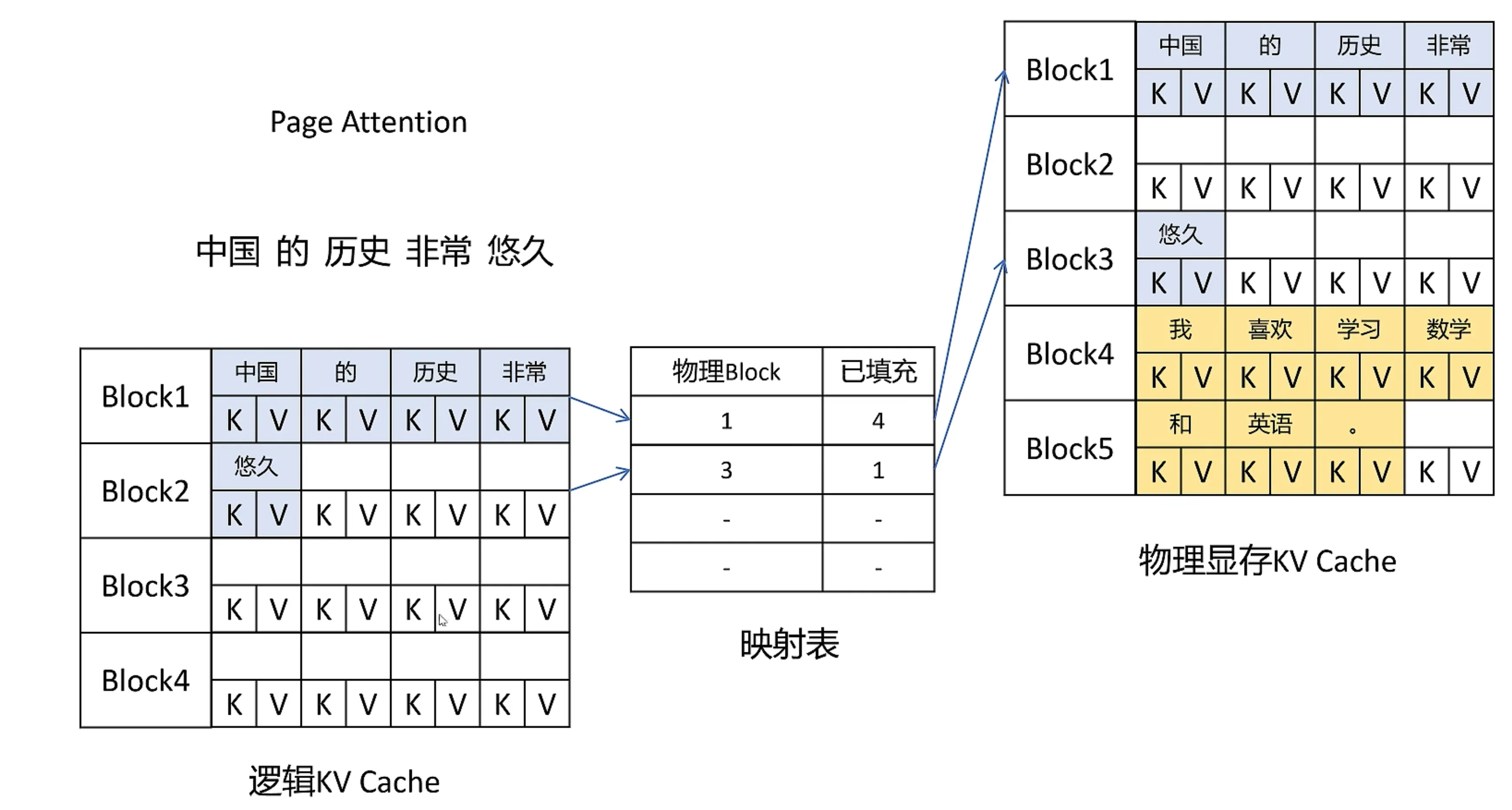
image-20250813000330631

Share KV Cache

copy on write机制：引用大于 1 的时候，不能直接写入，必须拷贝一份，再写入

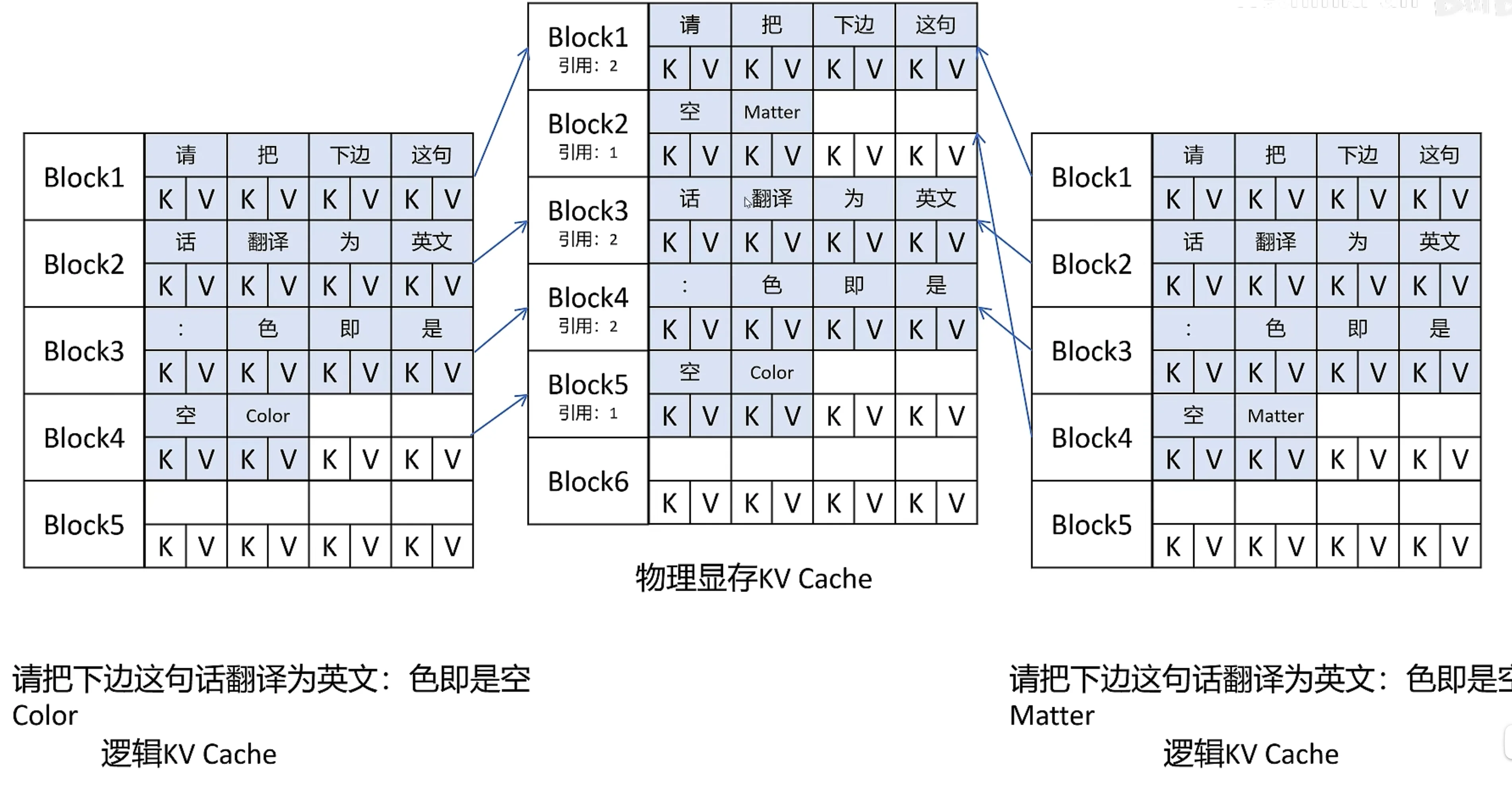
image-20250813001125290

还可以优化 beam-search

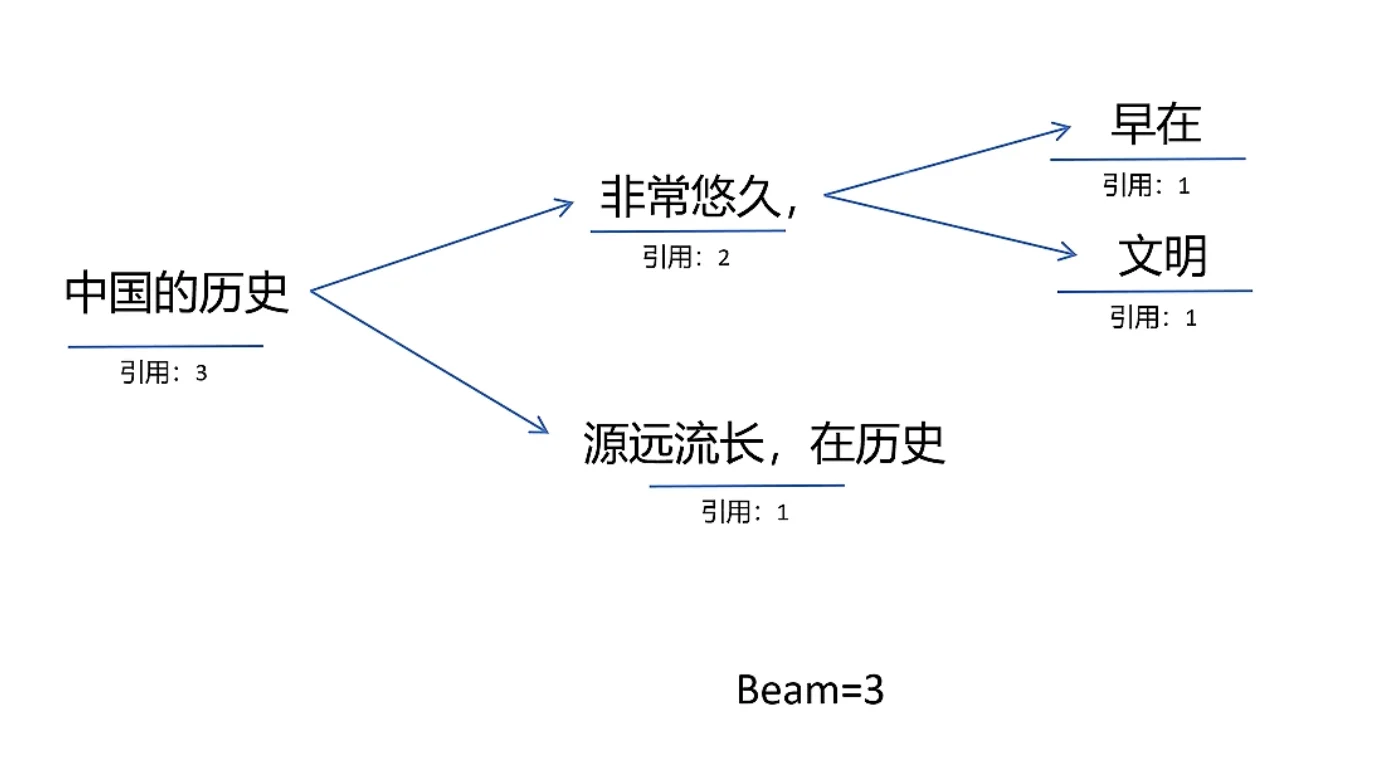
image-20250813001154648

Flash Attention

[2205.14135] FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

citationGitHub Repo stars

  • Fast
  • Memory-Efficient
  • Exact

为什么需要

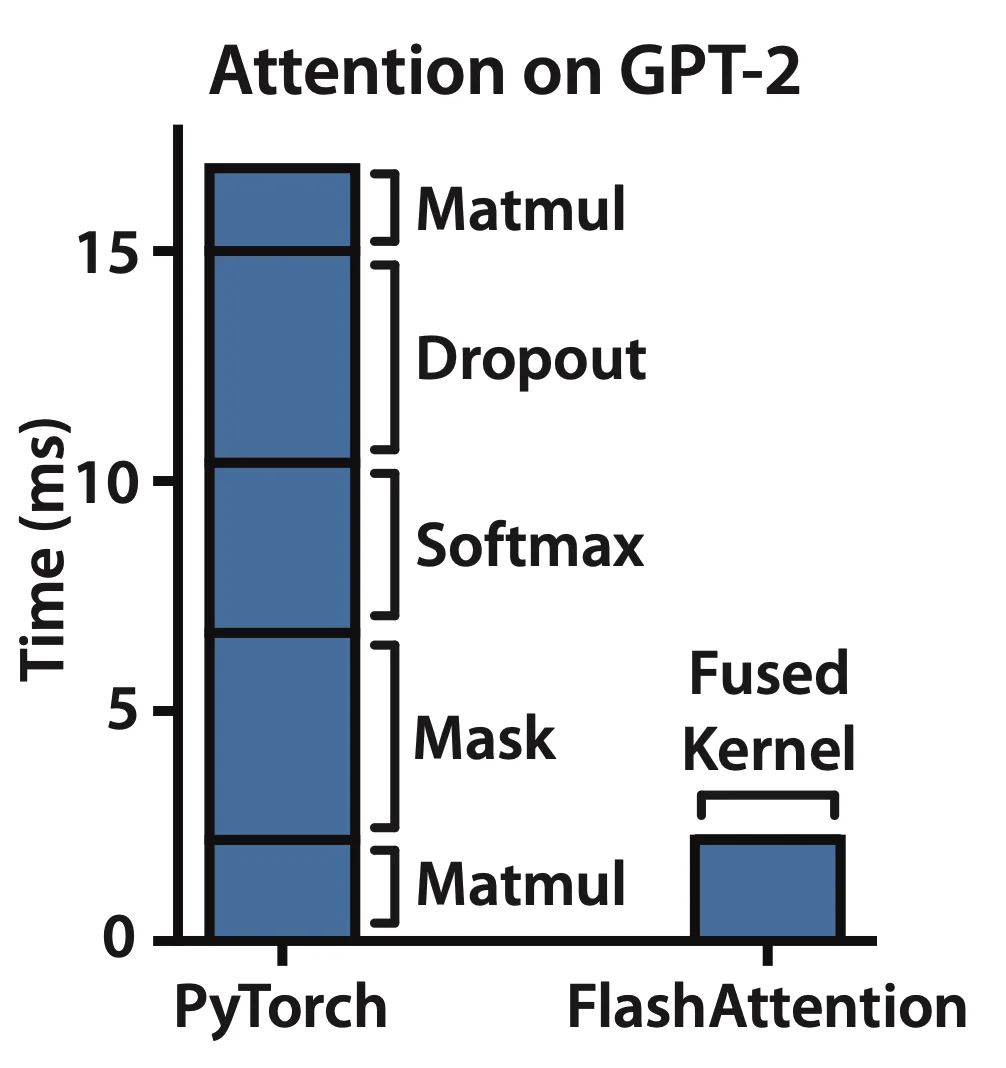
Transformers are slow and memory-hungry on long sequences, since the time and memory complexity of self-attention are quadratic in sequence length.

SRAM 读取快，HBM 读取慢

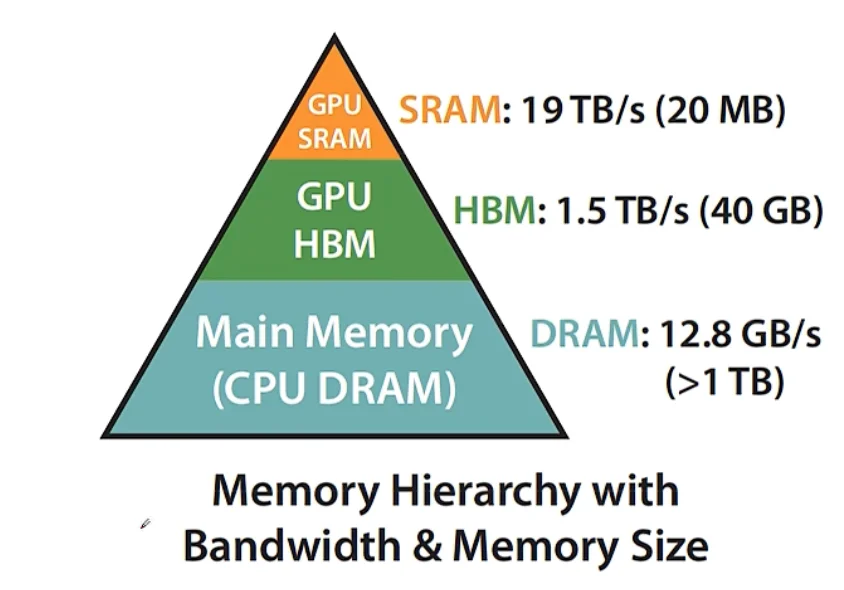
image-20250813002617202

  • Compute-bound: （数据等算力）
    • 大的矩阵乘法，多 channel 卷积
  • IO-bound:（算力等数据）
    • 按位操作：Relu，Dropout
    • 规约操作：sum、softmax

一般使用 fusion 融合操作，算结果时候只读取一次 HBM

原始 Attention 的实现

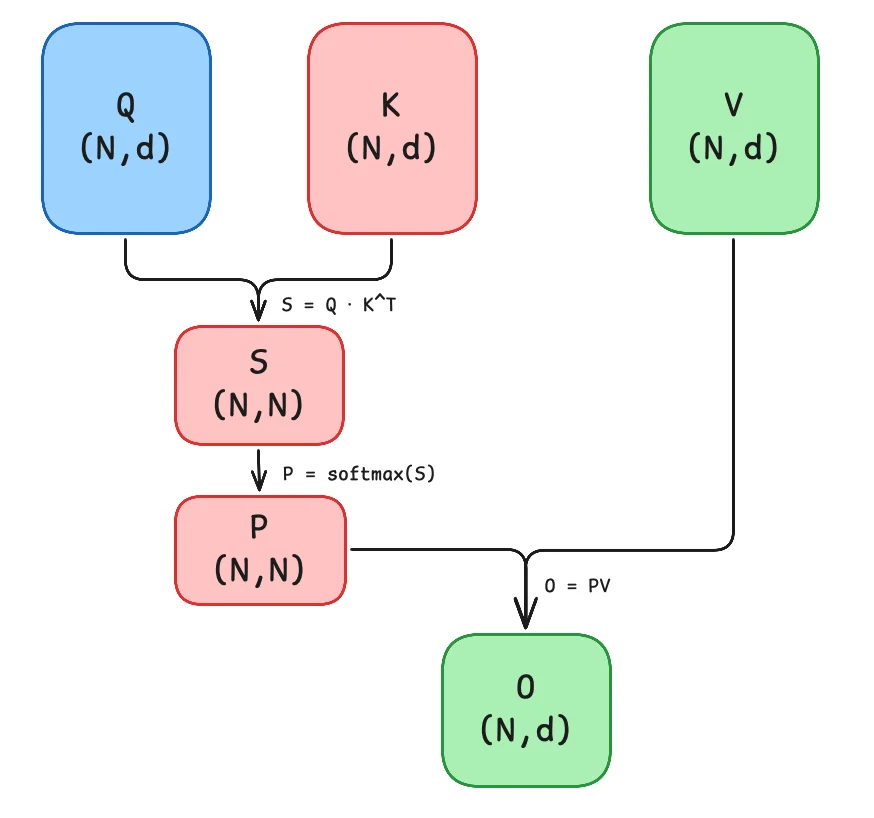
image-20250813143319708

矩阵 \(Q\), \(K\), \(V \in \mathbb{R}^{N\times d}\) 存储在 HBM。（\(N\) 是序列长度，\(d\) 是维度）

  1. 从 HBM 加载 \(Q\), \(K\) 到 SRAM
  2. 计算出 \(S = QK^T\)
  3. 将 \(S\) 写到 HBM
  4. 将 \(S\) 加载到 SRAM
  5. 计算 \(P = softmax(S)\)
  6. 将 \(P\) 写出到 HBM
  7. 从 HBM 加载 \(P\) 和 \(V\) 到 SRAM
  8. 计算 \(O = PV\)
  9. 把 \(O\) 写出到 HBM
  10. 返回 \(O\)

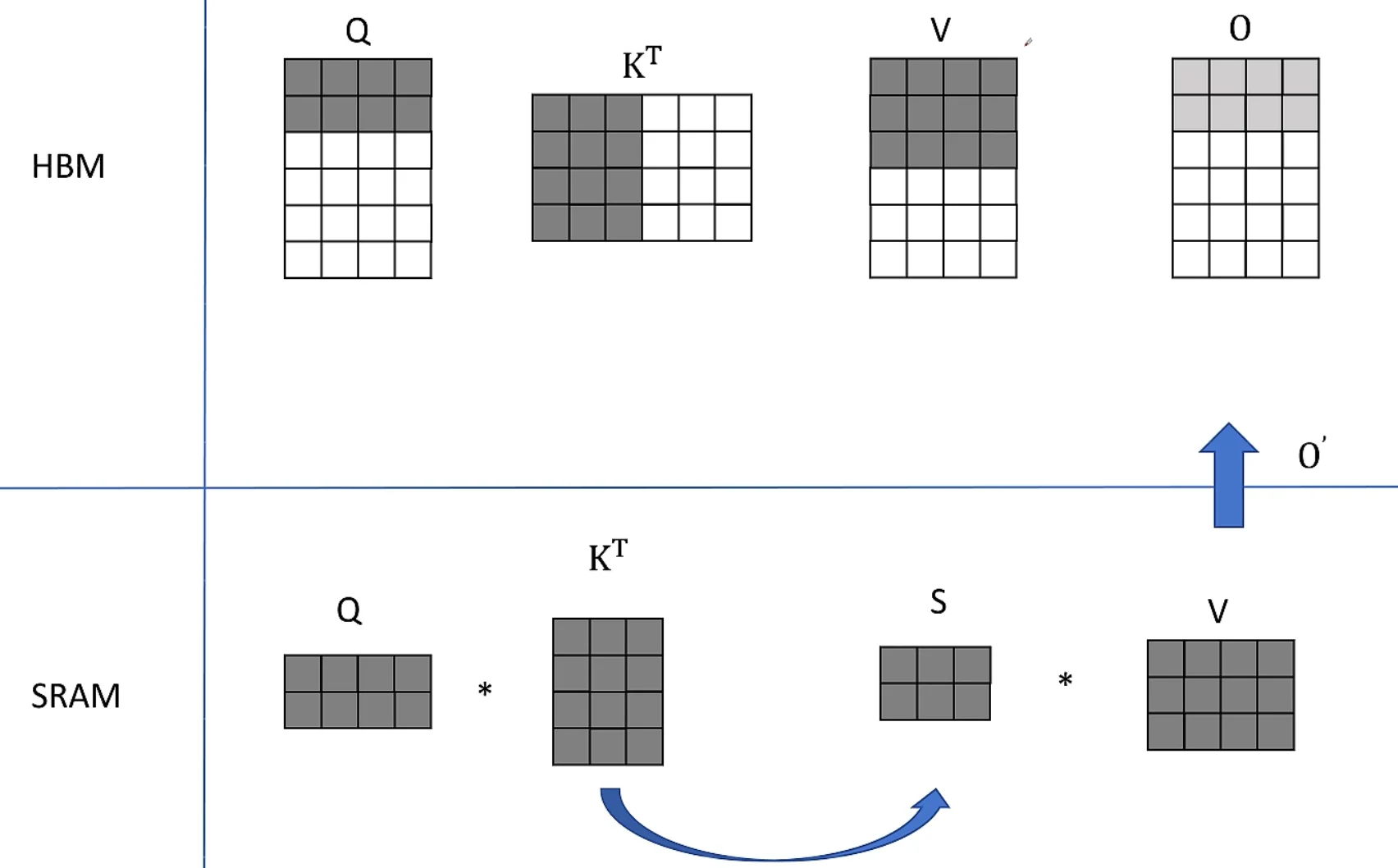
image-20250813142327972

tiling softmax

减少 IO 量

让 Attention 的所有计算都符合加法结合律

  • 通过分块计算，融合多个操作，减少中间结果缓存
  • 反向传播等时候，重新计算结果

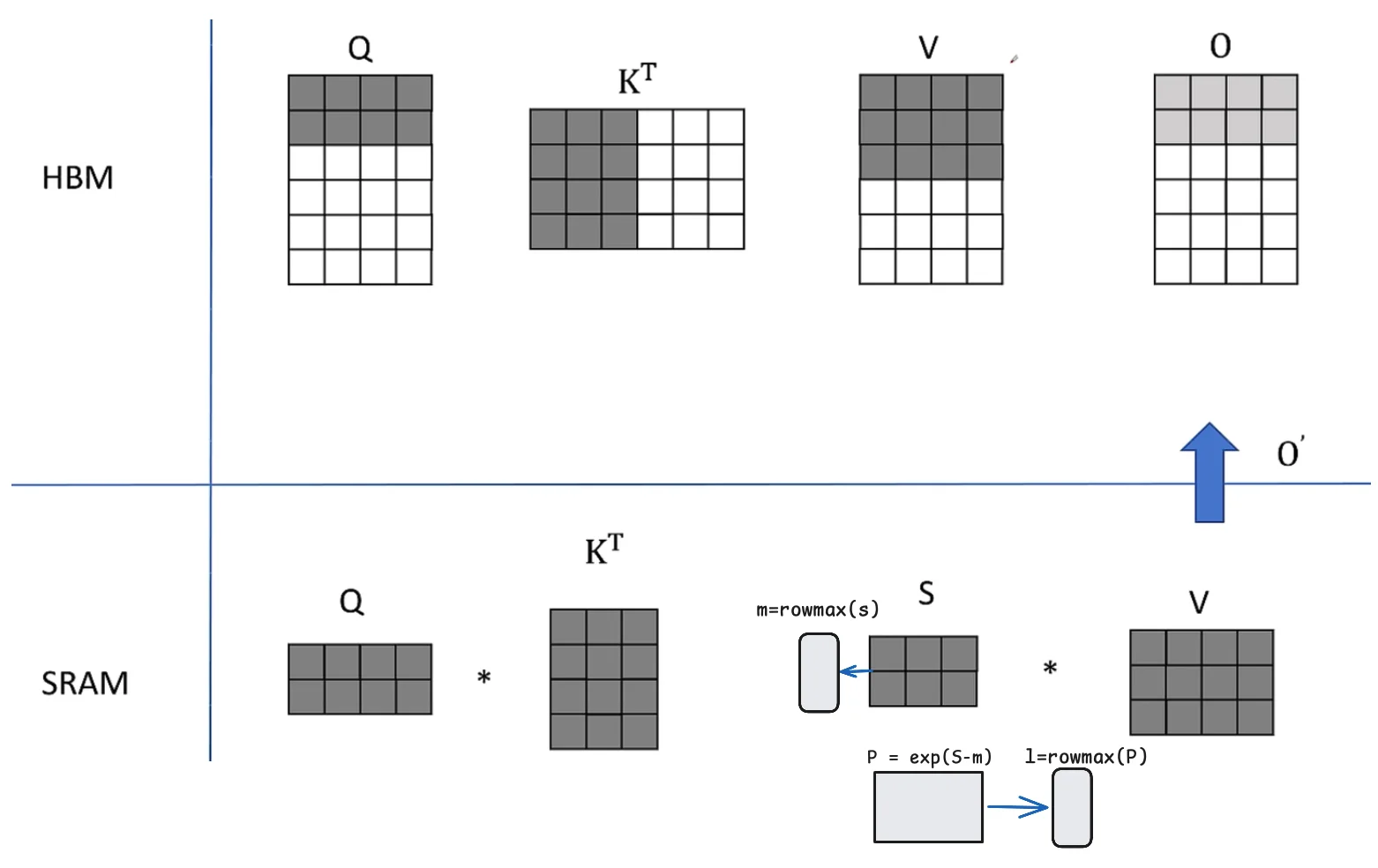
image-20250813002815635

softmax精度问题

\(e\) 的指数项可能超过精度，比如 65536

使用指数项可能会爆精，所以使用 safe_softmax

\[ \begin{aligned} m &= \max(x_1,...,x_N) \\ \mathrm{softmax}(\{x_1,...,x_N\}) &= \{\frac{e^{x_i}/e^m}{\sum_{j=1}^Ne^{x_j}/e^m}\}_{i=1}^N = \{\frac{e^{x_i-m}}{\sum_{j=1}^Ne^{x_j-m}}\}_{i=1}^N \end{aligned} \]

即如果计算了左侧的 softmax，右侧的 softmax 如何计算整体的

KV 在外循环 Q 在内循环

\[ \begin{aligned} & x = \lfloor x_1, \ldots, x_N, \ldots, x_{2N} \rfloor \\ & m(x) := \max(x) \quad \text{其中} \quad x = [x_1, \ldots, x_N] \\ & p(x) := [e^{x_1 - m(x)}, \ldots, e^{x_N - m(x)}] \\ & l(x) := \sum_i p(x)_i \\ & softmax(x) := \frac{p(x)}{l(x)} \end{aligned} \]

对于整体来讲

\[ \begin{aligned} & x^1 = [x_1, \ldots, x_N] \quad x^2 = [x_{N+1}, \ldots, x_{2N}] \\ & m(x) := \max(m(x^1), m(x^2)) \\ & p(x) := [e^{m(x^1) - m(x)} p(x^1), e^{m(x^2) - m(x)} p(x^2)] \\ & l(x) := e^{m(x^1) - m(x)} l(x^1) + e^{m(x^2) - m(x)} l(x^2) \\ & softmax(x) := \frac{p(x)}{l(x)} \end{aligned} \]
去掉最后一个 embedding 维度（4）
Q.shape[:-1] = (1, 1, 6)

[..., None] 会在最后增加一个维度，相当于：

(1, 1, 6) → (1, 1, 6, 1)

所以：

  • l.shape = (1, 1, Q_LEN, 1)
  • m.shape = (1, 1, Q_LEN, 1)
为什么是 (1, 1, Q_LEN, 1) 而不是 (1, 1, Q_LEN)？

作用：方便广播运算

在注意力计算时，l 和 m 是针对每个 query 位置存储的：

  • m → 这个位置的当前最大 logit（数值稳定 softmax 用）
  • l → 这个位置的 softmax 分母（sum(exp(...))）

在后续更新中，会用到像：

torch.exp(m_block_ij - mi_new)

这里的 m_block_ij 形状通常是 (1, 1, block_size, 1)， 如果 l 和 m 也有最后一个 1 维度，就可以无额外 reshape 直接广播。

另外一个原因：与 V 对齐

注意力输出是：

output = sum(softmax(QK^T) * V)

V 的形状是 (1, 1, KV_LEN, dim)， 而 l、m 只存每个 query 的一个标量，所以最后一维是 1， 这样在计算时既能和 (1, 1, Q_LEN, dim) 广播，也能和 (1, 1, Q_LEN, 1) 对齐。

需要额外存储

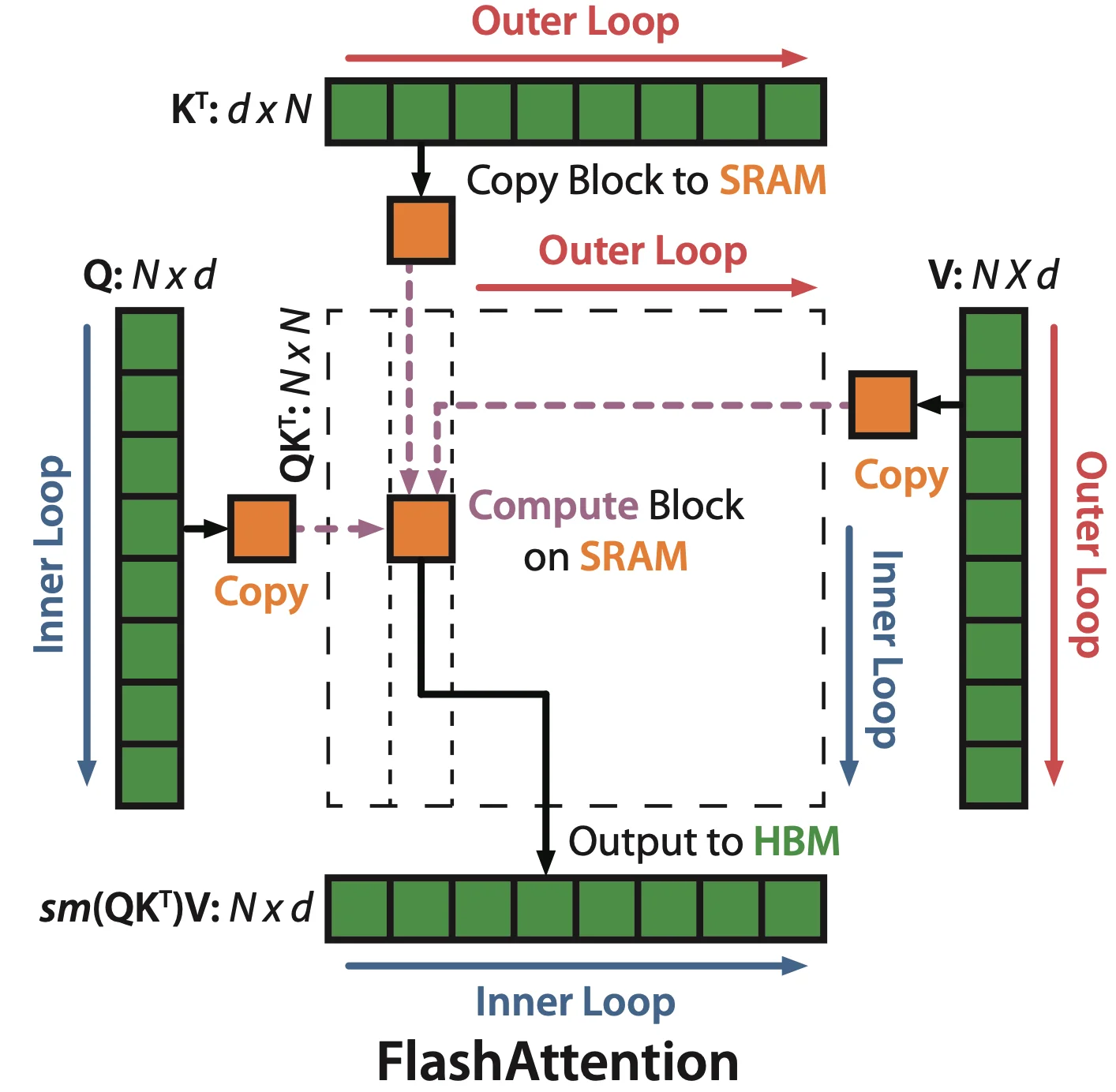
image-20250813003529043

image-20250813153517030

image-20250813142311190

反向传播 recomputation

前向的时候，会保存 softmax 统计值，\(m\) 和 \(l\)

image-20250813003543657

StreamLLM

在 nvidia-smi 中可以看到所有 GPU 的利用率会直接冲到 100%，直到这个超卡的请求全部生成完，才会恢复正常。这不就是典型的优先 prefill 暂停 decode 么，解决办法就是 chunked prefill size 啊，deepseek 都告诉你了。

评论