04 | 布朗运动 ¶

约 4091 个字 2 张图片预计阅读时间 16 分钟

Cheet Sheet¶

数字特征：

$\forall\;0\leq s<t\quad X(t)-X(s)\sim N(0,\sigma^2(t-s))$
- 正态分布的 pdf，在求特殊分布的时候有用

\[ f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \]

均值函数：$\mu_B(t)=0$
方差函数：$D_B(t)=t$
- $Var(A\pm B) = Cov(A\pm B,A\pm B) = Var(A) + Var(B) \pm 2Cov(A,B)$
自协方差函数：$C_B(t,s) =min(t,s)\qquad t,s>0$

性质：

写成增量的形式，增量之间互相独立

马尔科夫性：$B(t+\tau)-B(\tau)$ 也是标准布朗
自相似性：$\forall\;a\neq0\quad$ { $\frac1aB(a^2t);t\geq 0$ } 是标准布朗运动。
$0-\infty$对称性：$\overset{\sim}B(t)=\begin{cases}tB(\frac 1t)\quad t>0\\[2ex]0\qquad\quad t=0\end{cases}$ 则 { $\overset{\sim}B(t);t\geq0$ } 是标准布朗运动。

当遇到条件比现在大的情况如 $P(B(1)>1|B(2)=2)$ 一般都考虑使用相似或者对称性质进行求解，而不是使用贝叶斯

特殊分布：

首次击中时间：$P\left(\max_{s\leq t}B(s)\geq a\right) = P(T_a \leq t) = 2P(B(t)\geq a),\quad a > 0$

布朗桥

$X(t)=B(t)-tB(1)\quad 0\leq t \leq 1$

$X(0)=X(1)=0$ （桥的形状）
均值：$\mu_X(t)=0$
协方差：$C_X(s, t) = s(1 - t),\quad 0 < s < t < 1$

定义 ¶

直线上一质点每隔 $\Delta t$ 等概率向左或向右移动距离 $\Delta x$ ，且每次移动相互独立，$X(t)$ 为 $t$ 时刻质点的位置。

① $X(t)\sim N(0,\sigma^2)$

② $X(0)=0$

③ $\forall\;0\leq s<t\quad X(t)-X(s)\sim N(0,\sigma^2(t-s))$

样本轨道连续

独立增量

标准布朗运动的性质 ¶

齐次的独立增量过程
正态过程，分布完全由均值函数和自协方差函数确定

数字特征 * 均值函数：$\mu_B(t)=0$ * 方差函数：$D_B(t)=t$ * 自协方差函数：

  $$
  \begin{aligned}
  C_B(t,s) &= R_B(t,s) = D_B[\min (s,t)]\\
  &=min(t,s)\qquad t,s>0
  \end{aligned}
  $$

证明

我们考虑 $t \leq s$（不妨设 $t \leq s$，因为结果是对称的）：

我们将 $B(s)$ 拆成两个部分：

\[ B(s) = B(t) + (B(s) - B(t)) \]

将其代入协方差函数中：

\[ \begin{align*} \mathbb{E}[B(t) B(s)] &= \mathbb{E}[B(t)(B(t) + (B(s) - B(t)))]\\ &= \mathbb{E}[B(t)^2] + \mathbb{E}[B(t)(B(s) - B(t))]\\ &= \text{Var}(B(t)) + \mathbb{E}[B(t)]\mathbb{E}(B(s)-B(t))\\ &= t \end{align*} \]

注意：

$B(t)$ 与 $B(s) - B(t)$ 独立；
$\mathbb{E}[B(s) - B(t)] = 0$；
因为独立且后者期望为零，交叉项为 0。

因为我们设定 $t \leq s$，所以

\[ \mathbb{E}[B(t)B(s)] = \min(t,s) \]

布朗运动判定 ¶

布朗运动当且仅当它是正态过程，$E(B(t))=0$ 且 $E[B(t)B(s)]=t\wedge s.$

Markov 性 ¶

$\forall\;t\quad$ { $B(t+s)-B(t);s\geq 0$ } 是标准布朗运动。

起点的选取是任意的

证明

我们证明 $\{B(t); t \geq 0\}$ 是布朗运动。已知 $B(t)$ 是一个均值为 0，协方差函数为

\[ R_B(s,t) = \mathbb{E}[B(s)B(t)] = \min(s,t) \]

的随机过程。我们进行如下验证：

(1) 均值与方差

\[ \begin{aligned} \mathbb{E}[B(t) - B(s)] &= \mathbb{E}[B(t)] - \mathbb{E}[B(s)] = \mu_B(t) - \mu_B(s) = 0, \\ \mathbb{E}[(B(t) - B(s))^2] &= \mathbb{E}[B(t)^2] + \mathbb{E}[B(s)^2] - 2\mathbb{E}[B(t)B(s)] \\ &= R_B(t,t) + R_B(s,s) - 2R_B(t,s) \\ &= t + s - 2\min(t,s) = |t - s|. \end{aligned} \]

因此对于 $0 \leq s < t$，有

\[ B(t) - B(s) \sim \mathcal{N}(0, t - s). \]

(2) 独立增量

设任意的

\[ s_1 < t_1 \leq s_2 < t_2, \]

我们计算两个增量的协方差：

\[ \begin{aligned} \mathbb{E}[(B(t_1) - B(s_1))(B(t_2) - B(s_2))] &= \mathbb{E}[B(t_1)B(t_2)] - \mathbb{E}[B(s_1)B(t_2)] - \mathbb{E}[B(t_1)B(s_2)] + \mathbb{E}[B(s_1)B(s_2)] \\ &= R_B(t_1, t_2) - R_B(s_1, t_2) - R_B(t_1, s_2) + R_B(s_1, s_2) \\ &= \min(t_1, t_2) - \min(s_1, t_2) - \min(t_1, s_2) + \min(s_1, s_2) \\ &= t_1 - s_1 - t_1 + s_1 = 0. \end{aligned} \]

因此，增量 $B(t_1) - B(s_1)$ 与 $B(t_2) - B(s_2)$ 互相独立。

结合 $B(0) = 0$，可知 $\{B(t); t \geq 0\}$ 是具有独立增量的高斯过程。

(3) 正态过程

对任意整数 $n$ 和时间点

\[ 0 \leq t_1 < t_2 < \cdots < t_n, \]

考虑随机向量

\[ (B(t_1), B(t_2), \ldots, B(t_n)). \]

记增量为

\[ X_i = B(t_i) - B(t_{i-1}),\quad i=1,2,\ldots,n,\quad\text{其中 } t_0 := 0, \]

则

\[ (B(t_1), B(t_2), \ldots, B(t_n)) = (X_1, X_1 + X_2, \ldots, X_1 + \cdots + X_n), \]

是增量变量 $X_1, X_2, \ldots, X_n$ 的线性组合。

由于每个增量 $X_i$ 都服从正态分布且两两独立，因此整个向量服从多元正态分布。

故 $\{B(t); t \geq 0\}$ 是正态过程。

结论：

综上所述，$\{B(t); t \geq 0\}$ 是满足以下条件的随机过程：

$B(0) = 0$；
有独立增量；
每个增量 $B(t) - B(s) \sim \mathcal{N}(0, t - s)$；
是正态过程。

因此，$\{B(t); t \geq 0\}$ 是一个布朗运动。 $\blacksquare$

多元正太分布的线性变换依然是正态分布

自相似性 ¶

$\forall\;a\neq0\quad$ { $\frac1aB(a^2t);t\geq 0$ } 是标准布朗运动。

布朗运动的自相似性（self-similarity是它最核心、最优美的性质之一。在直觉上，它表达的是：

把布朗运动放大或缩小，看起来就像是原来的布朗运动。

自相似性是：

分形的核心特征（布朗运动是随机分形）
在金融中解释“不同时间尺度价格走势看起来相似”的数学基础
分析长时间行为时简化问题的重要工具

0 与 $\infty$ 对称性 ¶

令 $\overset{\sim}B(t)=\begin{cases}tB(\frac 1t)\quad t>0\\[2ex]0\qquad\quad t=0\end{cases}$ 则 { $\overset{\sim}B(t);t\geq0$ } 是标准布朗运动。

把布朗运动做“时间倒转 + 振幅缩放”，你又得到了一个标准布朗运动。

应用领域	举例说明
路径分析	某些 hitting time 与 maximum/minimum 问题在 0 和 ∞ 对称变换下形式不变
随机分形	说明布朗运动具有尺度不变性，是分形过程
金融建模	定价模型中分析小时间步和大时间尺度行为的一致性
理论物理	在量子场论中，布朗运动模型是路径积分的基础，体现“红外 - 紫外对称”思想

分形（Fractal）是一种数学和自然界中常见的结构，它具有局部和整体相似的特点，是许多复杂系统的本质特征。

虽然“分形”没有一个唯一公认的严格定义，但以下是 Benoît Mandelbrot（曼德博，分形理论之父）给出的经典定义之一：

一个几何形状，如果它的 Hausdorff 维数（分形维数）严格大于其拓扑维数，则称为分形。

图形	拓扑维数（整数）	分形维数（可为小数）
直线段	1	1
曼德博集	1	2
柯赫雪花曲线	1	≈ 1.2619
西尔皮斯基三角形	1	≈ 1.5849

所以“维数大于形状能容纳的维度”是分形的关键特征之一。

一个图形，在放大后细节仍然看起来和整体结构相似，且无限复杂，这种结构叫分形。

这种“局部与整体相似（自相似）”的性质，在自然界和数学中非常常见。

首次击中时 ¶

\[ \begin{aligned} \forall\;a>0\quad F_{T_a}(t)&=P(T_a\leq t) \end{aligned} \]

\[ \boxed{P\left(\max_{s\leq t}B(s)\geq a\right) = P(T_a \leq t) = 2P(B(t)\geq a)},\quad \text{对 } a > 0 \]

$\max_{s\leq t} B(s)$：布朗运动在时间区间 $[0,t]$ 中的最大值
$T_a = \inf\{s > 0 : B(s) = a\}$：布朗运动首次达到 $a$ 的时间
$B(t) \sim \mathcal{N}(0,t)$：在时间 $t$ 的布朗运动服从均值 0、方差 $t$ 的正态分布

直观解释

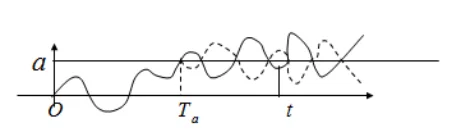
以价格为例，相当于求价格最高点不低于 / 不高于

左侧：$P(\max_{s\leq t}B(s)\geq a)$：表示“在时间 $t$ 以内，布朗运动是否曾经达到过或超过了 $a$”的概率。
中间：$P(T_a \leq t)$：布朗运动首次达到 $a$ 的时间是否早于或等于 $t$。这两个其实是同一件事：只要在 $[0,t]$ 里最大值超过了 $a$，那么 $T_a \leq t$。
右边：$P(B(t)\geq a)$：布朗运动在正好时刻 $t$ 达到 $a$ 或更高的概率。因为布朗运动是对称过程（正态分布对称），所以：

\[ P(B(t) \geq a) = P(B(t) \leq -a) \]

但我们要的是“曾经达到 $a$”的概率，远大于“正好在终点超过 $a$”的概率，因此乘 2：

\[ \boxed{P(\max_{s\leq t}B(s)\geq a) = 2P(B(t)\geq a)} \]

这个结果也叫做 反射原理（reflection principle） 的直接推论。

表达式	含义
$P(\max_{s\leq t} B(s) \geq a)$	布朗运动在 $[0,t]$ 曾超过 a 的概率
$P(T_a \leq t)$	首次达到 $a$ 的时间早于 $t$ 的概率
$2P(B(t) \geq a)$	利用布朗运动对称性 + 反射原理的结果

注意不同的形式：

最大值小于 $a$ 的概率

\[ \begin{aligned} P(\underset{0\leq s\leq t}{max}\,B(s)\leq a)&= 1-2P(B(t)\geq a)=2\Phi(\frac{\mid a\mid}{\sqrt t}) \end{aligned} \]

绝对值的形式：最小值一定小于 0，所以可以直接脱去绝对值符号
$X(t)=\mid \underset{0\leq s\leq t}{min}\,B(s)\mid = -\underset{0\leq s\leq t}{max}\,B_1(s)$

\[ \begin{align*} F_{X(t)}(y)=&P(X(t)\leq y)\overset{B_1(s)=-B(s)}{\longleftrightarrow}P(\underset{0\leq s\leq t}{max}\,B_1(s)\leq y)\\ =&1-2P(B_1(t)>y)\\ =&2\Phi(\frac y{\sqrt t})-1\qquad(t\geq 0) \end{align*} \]

对称性
$$ P(underset{0leq sleq t}{min},B(s)leq -y)=P(underset{0leq sleq t}{max},B(s)geq y) $$

换元

\[ \begin{aligned} P\{\underset{0\leq s\leq t}{max}\,\left[B(s)-B(t)\right]\leq x\}=&P\{\underset{0\leq s\leq t}{max}\,\left[B(t)- B(s)\right]\leq x\},\qquad x>0\\ =&P\{\underset{0\leq s\leq t}{max}\,B(t-s)\leq x\}\\ \overset{u = t-s}\longleftrightarrow &P\{\underset{0\leq u\leq t}{max}\,B(u)\leq x\}\\ =& 1-2P(B(t)\geq x) \end{aligned} \]

布朗桥运动 ¶

$X(t)=B(t)-tB(1)\quad 0\leq t \leq 1$

$X(0)=X(1)=0$

为正态过程

均值：

\[ \mu_X(t) = E[X(t)] = E[B(t) - tB(1)] = E[B(t)] - tE[B(1)] = 0 - t \cdot 0 = 0 \]

协方差（$0 < s < t < 1$）：

\[ \begin{align*} C_X(s, t) &= \operatorname{Cov}(X(s), X(t)) \\ &= \operatorname{Cov}(B(s) - sB(1),\; B(t) - tB(1)) \\ &= \operatorname{Cov}(B(s), B(t)) - t\operatorname{Cov}(B(s), B(1)) - s\operatorname{Cov}(B(1), B(t)) + st\operatorname{Cov}(B(1), B(1)) \\ &= \min(s, t) - t\min(s, 1) - s\min(1, t) + st \\ &= s - t s - s t + s t \\ &= s(1 - t) \end{align*} \]

例题 ¶

设 $\{B(t); t \geq 0\}$ 是标准布朗运动，则

\[ P\left( \max_{0 \leq s \leq 4} B(s) \geq 2 \right) = \underline{\qquad\qquad\qquad} \]

\[ P(B(3) < 3 \mid B(1) = 1, B(2) = 1) = \underline{\qquad\qquad\qquad} \]

设 $A \sim N(1,1)$，且 $A$ 与 $\{B(t); t \geq 0\}$ 独立，定义 $X(t) = B(t) + A t$，则：

$X(1)$ 服从 $\underline{\qquad\qquad\qquad}$ 分布，
$X(1) + X(2)$ 服从 $\underline{\qquad\qquad\qquad}$ 分布，
$\mathrm{Cov}(X(1) + X(2), X(1)) = \underline{\qquad\qquad\qquad}$

利用布朗运动最大值分布反射原理

\[ P\left( \max_{0 \leq s \leq t} B(s) \geq a \right) = 2 P(B(t) \geq a) = 2 \left(1 - \Phi\left(\frac{a}{\sqrt{t}}\right)\right) \]

取 $a=2, t=4$，得

\[ P\left( \max_{0 \leq s \leq 4} B(s) \geq 2 \right) = 2(1 - \Phi(1)) \approx 2 \times 0.1587 = 0.3174 \]

$(B(1), B(2), B(3))$ 是三元正态分布，条件分布计算后有

\[ P(B(3) < 3 \mid B(1) = 1, B(2) = 1) = P(B(1) < 3-1 = 2) = \Phi(2) = 0.98 \]

$X(1) + X(2) = B(1) + B(2) + 3A$

\[ \begin{align*} \mu &= \mu_{B(1)} + \mu_{B(2)} + 3\mu_A = 0 + 3 = 3\\ Var(B(1)+B(2)+3A) &= Var(B(1)) + Var(B(2))+Var(3A) + 2Cov(B(1),B(2))+2Cov(B(1),3A)+2Cov(B(2),3A)\\ &= 1+2 + 9 + 2 \min\{1,2\} + 0 + 0 (\text{独立})\\ &=14 \end{align*} \]

\[ \therefore X(1)+X(2) \sim N(3,14) \]

求协方差：

\[ \begin{aligned} \mathrm{Cov}(X(1) + X(2), X(1)) &= \mathrm{Cov}(X(1), X(1)) + \mathrm{Cov}(X(2), X(1))\\ &= \mathrm{Var}(X(1)) + \mathrm{Cov}(X(2), X(1))\\ &= 2 + \mathrm{Cov}(B(2)+2A,B(1)+A)\\ &= 2 + \mathrm{Cov}(B(2),B(1)) + 2\mathrm{Cov}(A,A)\\ &= 2 + \min\{2,1\} + 2\\ &= 5 \end{aligned} \]

设 { $B(t);t\geq0$ } 是标准布朗运动，则

（1）$B(3)-2B(1)$

服从 $N(0,3)$ 分布（$B(3)-2B(1)=B(3)-B(1)-B(1)\sim N(0,2+1)=N(0,3)$）

（2）$Cov(B(3)-2B(1),B(2))$

\[ \begin{aligned} Cov(B(3)-2B(1),B(2))&=Cov(B(3),B(2)) - 2Cov(B(1),B(2))\\ &=min\{3,2\} - 2\min\{2,1\} = 0 \end{aligned} \]

（3）$P(B(5.5)>5\mid B(1.1)=3,B(1.5)=1)$

转化成增量形式进行计算

\[ \begin{aligned} P(B(5.5)>5\mid B(1.1)=3,B(1.5)=1)&=P(B(5.5)-B(1.5)>4)\\ &=1-\Phi(2)=0.02 \end{aligned} \]

（4）$P(\underset{0\leq t\leq6.25}{max}\,B(t)<2.5)$

\[ \begin{aligned} P(\underset{0\leq t\leq6.25}{max}\,B(t)<2.5)&=1-P(\underset{0\leq t\leq6.25}{max}\,B(t)\geq2.5)\\ &=1-2[1-P(B(6.25)<2.5)]\\ &=2\Phi(1)-1=0.68 \end{aligned} \]

相似性 ¶

设 $\{B(t),t\geq0\}$ 是标准布朗运动，求

(1) $P\{B(0.5)\leq1|B(1)=1,B(2)=2\}$;

解：$\{B(t);t\geq0\}$ 是标准布朗运动 . 又 $B(t)=t\bar{B}(1/t)$, 所以

\[ P\{B(0.5)\leq1|B(1)=1,B(2)=2\}\\ =P\{0.5\bar{B}(2)\leq1|\bar{B}(1)=1,2\bar{B}(0.5)=2\}\\ =P\{\bar{B}(2)\leq2|\bar{B}(1)=1,\bar{B}(0.5)=1\}\\ =P\{\bar{B}(2)-\bar{B}(1)\leq1\}=\Phi(1)=0.8413 \]

(2) 在 $B(1)=1,B(2)=2$ 的条件下，$B(0.5)$ 服从什么分布？

即是在 $\bar{B}(1)=1,\bar{B}(0.5)=1$ 的条件下，

\[ \bar{B}(2)=1+(\bar{B}(2)-\bar{B}(1))\sim N(1,1) \]

所以 $B(0.5)=0.5\bar{B}(2)\sim N(0.5,0.25)$.

例题

$\{cB(t/4);\, t\geq0\}$ 仍是标准布朗运动的充要条件是 $c=$ ( )

(A) $\pm\frac{1}{2}$ (B) $\pm\frac{1}{4}$ (C) $\pm2$ (D) $\pm4$

答案：C

解析：

利用布朗运动的自相似性：$\forall\, a>0,\ \left\{\frac{1}{a}B(a^2 t);\, t\geq0\right\}$ 仍是标准布朗运动。

题中 $t \mapsto t/4$，即 $a^2 t = t/4 \implies a = 1/2$，所以

\[ \left\{\frac{1}{a}B(a^2 t)\right\} = \left\{2B(t/4)\right\} \]

仍是标准布朗运动。

因此 $c = \pm 2$，选 C。

条件分布的问题，使用 markov 性质和独立增量性质进行构造，注意这里会有自相似和对称性质的应用，均值会改变

6. 在 $B(1)=1$ 的条件下，$B(2)$ 的条件分布函数 $F_{B(2)|B(1)}(x|1)$ 为 ( )

(A) $\Phi(x)$ (B) $\Phi(x-1)$ (C) $\Phi(x+1)$ (D) $\Phi\left(\frac{x-1}{2}\right)$

解析：
$B(2)|B(1)= B(2) - B(1)+B(1) = 1 + N(0,1) \sim N (1,1)$，所以分布函数为 $\Phi\left(\frac{x-1}{1}\right)$，即选 (B)。

7. 在 $B(2)=2$ 的条件下，$B(1)$ 的条件密度函数 $f_{B(1)|B(2)}(x|2)$ 为 ( )

(A) $\sqrt{2}\varphi\left(\frac{x-1}{0.5}\right)$
(B) $\sqrt{2}\varphi\left(\frac{x-1}{\sqrt{0.5}}\right)$
(C) $\varphi\left(\frac{x-1}{0.5}\right)$
(D) $\varphi\left(\frac{x-1}{\sqrt{0.5}}\right)$

解析：

先应用 $0 \sim \infty$ 对称性 , 令 $B(t) = t\widetilde{B}(\frac{1}{t})$（注意这种写法，比较重要）

所以可以得到条件分布函数为

\[ \begin{align*} F_{B(1)|B(2)}(x|2) &= P\{B(1)\leq x|B(2)=2\} \\ &= P\{\widetilde{B}(1)\leq x | \widetilde{B}(\frac12)=1\} \\ &= P\{\widetilde{B}(1) - \widetilde{B}(\frac12)\leq x -1\} \\ &= \Phi\left(\frac{x-1}{\sqrt{0.5}}\right) \end{align*} \]

但是需要注意的是，这里求得是 pdf，所以需要对分布函数 $F_{B(1)|B(2)}(x|2)$ 求导

\[ f_{B(1)|B(2)}(x|2) = \frac{d}{dx}F_{B(1)|B(2)}(x|2) = \frac{1}{\sqrt{0.5}} \varphi\left(\frac{x-1}{\sqrt{0.5}}\right) = \sqrt{2}\varphi\left(\frac{x-1}{\sqrt{0.5}}\right) \]

所以选 (B)。

首次击中时 ¶

脑子里回想正态分布 pdf 的图像

击中时 + 绝对值

\[ P\left\{|\min_{1\leq t\leq 2} B(t)| \geq 2 \mid B(1)=0\right\} = \]

(A) 0.02 (B) 0.04 (C) 0.96 (D) 0.98

解析：

$\Phi(0.5) = 0.69,\Phi(1)=0.84,\Phi(2)=0.98,\Phi(2.5)=0.99$

\[ \begin{align*} P\left\{|\min_{1\leq t\leq 2} B(t) |\geq 2 \mid B(1)=0\right\} &=P\left\{-\min_{1\leq t\leq 2} B(t) - B(1) \ge 2 \right\} \quad \text{脱去绝对值}\\ &= P \left\{ -\min_{0\leq t\leq 1} B(t)\ge 2 \right\}= P \left\{ \min_{0\leq t\leq 1} B(t)\le -2 \right\} \quad \text{反射原理}\\ &= P \left\{ \max_{0\leq t\leq 1} B(t)\ge 2 \right\} \\ &= 2\cdot P \left\{ B(1)\ge 2 \right\} \\ &=2(1-\Phi(2)) = 0.04 \end{align*} \]

所以选 B

布朗桥 ¶

例题

已知 $B(t)$ 是一个标准布朗运动，请回答以下问题：

(1) $2B(1)-B(2)$ 符合什么分布？

(2) 证明 $(t+1)B\left(\frac{1}{t+1}\right)-B(1)$ 也是标准布朗运动。

(3) 求 $P\{B(1)>1|B(2)=2,B(114)=514\}$。

(4) 求 $P\{\min_{1\leq s\leq2}B(t)\leq-2|B(1)=-1\}$。

(5) 设 $X(t)=\{B(t),0<t<1|B(1)=0\}$，计算 $D_X(t)$。

答案：

(1) $N(0,2)$

解析： $2B(1) \sim N(0,4)$，$B(2) \sim N(0,2)$，且 $\operatorname{Cov}(2B(1),B(2)) = 2\operatorname{Cov}(B(1),B(2)) = 2$。

因此 $\operatorname{Var}(2B(1)-B(2)) = 4 + 2 - 2 \times 2 = 2$，所以 $2B(1)-B(2) \sim N(0,2)$。

(2) 书上两个定理结合下

解析：

法 1：使用性质 1 进行证明

性质 1 设 $\{X(t);t\geqslant0\}$ 是一样本轨道连续的随机过程，则 $\{X(t);t\geqslant0\}$ 是标准布朗运动当且仅当它是正态过程且 $\mu_X(t)=0,R_X(s,t)=\min\{s,t\}.$

设 $X(t) = (t+1)B(\frac{1}{t+1}) - B(1)$，需要证明 $X(t)$ 是标准布朗运动。

首先证明 $X(t)$ 是正态过程：
- $B(\frac{1}{t+1})$ 是正态过程
- $B(1)$ 是正态随机变量
- 因此 $X(t)$ 是正态过程
计算均值函数： $$ begin{align} E[X(t)] &= E[(t+1)B(frac{1}{t+1}) - B(1)] \ &= (t+1)E[B(frac{1}{t+1})] - E[B(1)] \ &= 0 end{align} $$
计算自相关函数： $$ begin{align} R_X(s,t) &= E[X(s)X(t)] \ &= E[(s+1)B(frac{1}{s+1}) - B(1)][(t+1)B(frac{1}{t+1}) - B(1)] \ &= (s+1)(t+1)E[B(frac{1}{s+1})B(frac{1}{t+1})] - (s+1)E[B(frac{1}{s+1})B(1)] - (t+1)E[B(frac{1}{t+1})B(1)] + E[B^2(1)] \ &= (s+1)(t+1)min(frac{1}{s+1},frac{1}{t+1}) - (s+1)min(frac{1}{s+1},1) - (t+1)min(frac{1}{t+1},1) + 1 \ &= min(s+1,t+1) - min(s+1,1) - min(t+1,1) + 1 \ &= min(s+1,t+1) - 1\ &= min(s,t) end{align} $$

因此，$X(t)$ 是标准布朗运动。

法二：使用性质 2 的组合进行证明

利用布朗运动的自相似性和时间反转性质：

markov 性质：$B(t+\tau)-B(\tau)$ 是标准布朗运动
时间反转：$\{tB(1/t); t > 0\}$ 是标准布朗运动

步骤

\[ \begin{align*} &\because \{B(t)\} \text{ 是标准布朗运动} \\ &\because \text{Markov性质：} \{B(t+\tau)-B(\tau)\} \text{ 是标准布朗运动} \\ &\therefore \{B(t+1)-B(1)\} \text{ 是标准布朗运动} \\ &\because \text{时间反转：} \{tB(1/t)\} \text{ 是标准布朗运动} \\ &\therefore \{(t+1)B(\frac{1}{t+1})-B(1)\} \text{ 是标准布朗运动} \\ &\blacksquare \end{align*} \]

(3) $\frac{1}{2}$ 解析：

\[ P\{B(1)>1|B(2)=2,B(114)=514\} = P\{B(1)>1|2B(\frac12)=2,114B(\frac1{114})=514\}\\ = P\{B(1)>1|B(\frac12)=1\} \]

在 $B(\frac12)=1$ 的条件下，$B(1)$ 服从

\[ \begin{align*} B(1) &= B(1) - B(\frac12) + B(\frac12)\\ &= N(0,\frac12) + 1\\ &= N(1,\frac12) \end{align*} \]

所以 $P(B(1)>1| B(\frac12)=1) = 0.5$

(4) $0.32$

解析：

由反射原理

\[ \begin{align*} P\{\min_{1\leq t\leq2}B(t)\leq-2|B(1)=-1\} &= P\{\max_{1\leq t\leq2}B(t)-B(1)\geq 1\} \\ &= P\{max_{0\leq t\leq1}B(t)\geq 1\} \\ &= 2[P\{B(1)\geq 1\}] \\ &= 2[1-\Phi(1)] \\ &= 2[1-0.84]= 0.32 \end{align*} \]

(5) $t(1-t)$

解析：

在 $B(1)=0$ 条件下，$X(t) = B(t) - tB(1)$，

而布朗桥运动的协方差为 $C_X(s, t) = s(1 - t),\quad 0 < s < t < 1$

所以 $D_X(t) = C_x(t,t) = \operatorname{Var}(B(t)) + t^2\operatorname{Var}(B(1)) - 2t\operatorname{Cov}(B(t),B(1)) = t + t^2 - 2t^2 = t(1-t)$。

注：第五题是布朗桥过程，这部分容易被忽视。

数字特征求解与特殊 ¶

已知 $B(t)$ 是标准正态函数，则 $\sum_{k=1}^{n}B(k)$ 符合_ 分布，$X(t)=e^{B(t)}$ 的均值函数是_。

解析：

$\sum_{k=1}^{n}B(k)$ 符合 $N(0,\frac{k(k+1)(2k+1)}{6})$ 分布，$X(t)=e^{B(t)}$ 的均值函数是 $e^{\frac{t}{2}}$

对于布朗运动 $B(t)$，我们知道 $B(k) \sim \mathcal{N}(0, k)$，并且 $B(k)$ 与 $B(k-1)$ 不独立（因为是一个过程）；改写成增量的形式

\[ B(k) = \sum_{i=1}^{k} \left[ B(i) - B(i-1) \right], \text{ 其中 } B(i)-B(i-1) \sim \mathcal{N}(0,1), \text{ 相互独立} \]

所以 $\sum_{k=1}^n B(k)$ 是这些正态变量的线性组合。我们将其写为：

\[ \begin{align*} \sum_{k=1}^n B(k) &= \sum_{k=1}^n \sum_{j=1}^k (B(j) - B(j-1)) = \sum_{j=1}^n (n - j + 1)(B(j) - B(j-1))\\ &= \sum_{j=1}^n (n - j + 1) \cdot \Delta B_j, \quad \Delta B_j := B(j) - B(j-1) \end{align*} \]

因为每个 $\Delta B_j \sim \mathcal{N}(0, 1)$ 且独立 ⇒ 此和是均值为 0 的正态分布

方差为：

\[ \operatorname{Var} \left( \sum_{j=1}^n (n - j + 1) \cdot \Delta B_j \right) = \sum_{j=1}^n (n - j + 1)^2\\ = \sum_{k=1}^n k^2 = \frac{n(n+1)(2n+1)}{6} \]

对数正态分布的均值函数是

\[ E[e^X] = e^{\mu + \frac{1}{2}\sigma^2} \]

而 $B(t)$ 的均值是 0，$\sigma^2 = t$

带入公式即可

对数正态分布均值求解

以下推导过程摘选自 x 服从正态分布 , 求 e^x 的期望？ - 知乎

如果 $f(x)$ 是随机变量 $X$ 的概率密度函数，那么我们有如下引理：

\[ E[g(X)] = \int_{-\infty}^{\infty} g(x) f(x) dx \]

在我们的问题里，$X \sim N(\mu, \sigma^2)$，所以

\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

根据引理，我们可以得：

\[ E[e^X] = \frac{1}{\sigma \sqrt{2\pi}} \int_{-\infty}^{\infty} e^x e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx \]

让我们对 $e^x e^{-\frac{(x-\mu)^2}{2\sigma^2}}$ 做一些调整可得：

\[ = e^{x-\frac{(x-\mu)^2}{2\sigma^2}} = e^{\mu + \frac{1}{2}\sigma^2} e^{x-\mu - \frac{1}{2}\sigma^2 - \frac{(x-\mu)^2}{2\sigma^2}} = e^{\mu + \frac{1}{2}\sigma^2} e^{-\frac{(x-\sigma^2)-\mu}{2\sigma^2}} \]

这个时候，

\[ E[e^X] = \frac{1}{\sigma \sqrt{2\pi}} \int_{-\infty}^{\infty} e^{\mu + \frac{1}{2}\sigma^2} e^{-\frac{(x-\sigma^2)-\mu}{2\sigma^2}} dx\\ = e^{\mu + \frac{1}{2}\sigma^2} \int_{-\infty}^{\infty} \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\sigma^2)-\mu}{2\sigma^2}} dx\]

令 $t = x - \sigma^2$，我们有：

\[ E[e^X] = e^{\mu + \frac{1}{2}\sigma^2} \int_{-\infty}^{\infty} \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt \]

右边这个项 $\int_{-\infty}^{\infty} \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt$ 是不是似曾相识？它其实是一个服从 $N(\mu, \sigma^2)$ 的随机变量的累积分布函数 (CDF)，所以

\[ \int_{-\infty}^{\infty} \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt = 1 \]

所以我们可以得到

\[ E[e^X] = e^{\mu + \frac{1}{2}\sigma^2} \]

在这里 $X \sim N(\mu, \sigma^2)$。

方法 2：用 Moment Generating Function 来解释

让我们用 $M_X(t)$ 表示随机变量 $X$ 的 Moment Generating Function，这里 $t \in \mathbb{R}$ 。那我们有

\[ M_X(t) = E(e^{tX}) \]

如果随机变量 $X \sim N(\mu, \sigma^2)$ ，那我们有

\[ M_X(t) = E(e^{tX}) = e^{t\mu + \frac{t^2}{2}\sigma^2} \]

当 $t = 1$ 的时候，即 $E(e^X) = e^{\mu + \frac{1}{2}\sigma^2}$ 。

2. $B(2) + B(1)$ 服从下列什么分布？

(A) $N(0,1)$ (B) $N(0,3)$ (C) $N(0,5)$ (D) $N(0,6)$

解析：
$B(2)$ 和 $B(1)$ 联合正态，$B(2) \sim N(0,2)$，$B(1) \sim N(0,1)$，且 $\operatorname{Cov}(B(2), B(1)) = 1$。

\[ \operatorname{Var}(B(2) + B(1)) = \operatorname{Var}(B(2)) + \operatorname{Var}(B(1)) + 2\operatorname{Cov}(B(2), B(1)) = 2 + 1 + 2 \times 1 = 5 \]

所以选 (C)。

例题 - pdf - 公式记忆

$B(2)$ 的密度函数 $f_{B(2)}(x)$ 为 ( )

(A) $\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$
(B) $\frac{1}{2\sqrt{\pi}}e^{-\frac{x^2}{2}}$
(C) $\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{4}}$
(D) $\frac{1}{2\sqrt{\pi}}e^{-\frac{x^2}{4}}$

解析：
$B(2) \sim N(0,2)$，标准正态密度调整方差为 $2$，即

\[ f(x) = \frac{1}{\sqrt{2\pi \cdot 2}} e^{-\frac{x^2}{2 \cdot 2}} = \frac{1}{2\sqrt{\pi}} e^{-\frac{x^2}{4}} \]

所以选 (D)。

独立增量拆分

已知标准布朗分布 $\{B(t);t\geq0\}$, 求 $E(B(2)B(4)B(6))$

\[ \begin{aligned} &\text{设 } A = B_2,\quad X = B_4 - B_2,\quad Y = B_6 - B_4 \\ &\text{则 } B_4 = A + X,\quad B_6 = A + X + Y \\ \mathbb{E}[B_2 B_4 B_6] &= \mathbb{E}[A (A + X)(A + X + Y)] \\ &= \mathbb{E}\left[ A(A + X)^2 + A(A + X)Y \right] \\ &= \mathbb{E}\left[ A^3 + 2A^2 X + A X^2 + A^2 Y + A X Y \right] \\ &= \mathbb{E}[A^3] + 2\mathbb{E}[A^2 X] + \mathbb{E}[A X^2] + \mathbb{E}[A^2 Y] + \mathbb{E}[A X Y] \\ &= 0 + 2 \cdot \mathbb{E}[A^2] \cdot \mathbb{E}[X] + \mathbb{E}[A] \cdot \mathbb{E}[X^2] + \mathbb{E}[A^2] \cdot \mathbb{E}[Y] + \mathbb{E}[A] \cdot \mathbb{E}[X Y] \\ &= E(A^3) = E(B^3(2)) \end{aligned} \]

$A$ 对称正态，奇次中心矩为 $0$

证明

我们来推导一个对称正态随机变量（如 $A \sim \mathcal{N}(0, \sigma^2)$）的奇数阶矩为 0，即：

设 $A \sim \mathcal{N}(0, \sigma^2)$，其概率密度函数为：

\[ f_A(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{x^2}{2\sigma^2} \right) \]

\[ \mathbb{E}[A^{2k+1}] = \int_{-\infty}^{\infty} x^{2k+1} f_A(x) \, dx \]

将 $f_A(x)$ 代入：

\[ \mathbb{E}[A^{2k+1}] = \int_{-\infty}^{\infty} x^{2k+1} \cdot \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{x^2}{2\sigma^2} \right) dx \]

被积函数：$x^{2k+1} \cdot \exp\left( -\frac{x^2}{2\sigma^2} \right)$ 是奇函数

$x^{2k+1}$ 是奇函数
$\exp\left( -\frac{x^2}{2\sigma^2} \right)$ 是偶函数
奇 × 偶 = 奇

奇函数在对称区间上积分为 0：

\[ \int_{-\infty}^{\infty} \text{奇函数}(x) \, dx = 0 \]

因此：

\[ \boxed{\mathbb{E}[A^{2k+1}] = 0} \]

因此：

\[ \boxed{\mathbb{E}[B_2 B_4 B_6] = 0} \]

也可以看 98 上的讨论随机过程布朗运动一道题 - CC98 论坛令X=B2，Y=B4-B2，Z=B6-B4，三者独立同分布N(0, 2)，然后把均值里面的三项乘开分别求。有XYZ的奇数次幂的项都为0（因为写成积分的话是个奇函数），结果算了个0

习题

已知 $X(t) = \cos (t + \Theta) + e^{-t} B(e^{2t})$，其中 $\Theta \sim U(0, 2\pi)$，$B(t)$ 为标准布朗运动，且 $\Theta$ 与 $B(t)$ 相互独立。

(1) 计算均值函数与自协方差函数，并证明 $\{X(t)\,|\, -\infty < X(t) < +\infty\}$ 是平稳分布。

(2) 判断是否有均值的各态历经性。

(3) 求其功率谱函数。

答：

\[ \begin{align*} &(1)\quad 0,\quad C_X(\tau) = \frac{1}{2}\cos\tau + e^{-|\tau|} \\ &(2)\quad \text{不具有均值的各态历经性} \\ &(3)\quad S_X(\omega) = \frac{2}{\omega^2+1} + \pi[\delta(\omega+1)+\delta(\omega-1)] \end{align*} \]

解答过程：

(1) 计算均值函数与自协方差函数

先计算均值函数：

\[ E[X(t)] = E[\cos(t+\Theta)] + E[e^{-t}B(e^{2t})]\\ = 0 + e^{-t} \cdot 0 =0 \]

再计算自协方差函数

这里计算过程中用到的 Brown 的性质比较关键

\[ \begin{align*} E[X(t)X(s)] &= E\left[\left(\cos(t+\Theta) + e^{-t}B(e^{2t})\right)\left(\cos(s+\Theta) + e^{-s}B(e^{2s})\right)\right] \\ &= E[\cos(t+\Theta)\cos(s+\Theta)] + E[e^{-t}B(e^{2t})e^{-s}B(e^{2s})] + E[\cos(t+\Theta)]E[e^{-s}B(e^{2s})] + E[\cos(s+\Theta)]E[e^{-t}B(e^{2t})] \\ &=\frac{1}{2} \cos(t-s) + e^{-(t+s)}E(B(e^{2t})B(e^{2s}))\\ &= \frac{1}{2} \cos(\tau)+e^{-(t+s)}\min(e^{2t}, e^{2s})\\ &= \frac{1}{2} \cos(\tau)+ e^{-|t-s|} \quad \text{可分 $t \geq s$ 和 $t < s$ 两种情况验证} \end{align*} \]

由于 $\Theta$ 与 $B(t)$ 独立，且 $E[\cos(t+\Theta)] = 0$，$E[B(\cdot)] = 0$，所以后两项为 0。

\[ C_X(t,s) = \frac{1}{2}\cos(t-s) + e^{-|t-s|} \]

由于 $C_X(t,s)$ 只与 $t-s$ 有关，且均值为常数，故 $X(t)$ 是平稳分布。

(2) 判断是否有均值的各态历经性

由于 $X(t)$ 包含 $\cos(t+\Theta)$ 项，$\Theta$ 是随机常数，导致 $X(t)$ 的均值对不同样本轨道不一样，因此不具有均值的各态历经性。

(3) 求其功率谱函数

功率谱为自相关函数的傅里叶变换：

又因为均值为 0，所以自相关等于自协方差

$\frac{1}{2}\cos(t-s)$ 的谱为 $\frac{\pi}{2}[\delta(\omega+1)+\delta(\omega-1)]$
$e^{-|t-s|}$ 的谱为 $\frac{2}{\omega^2+1}$

所以

\[ S_X(\omega) = \frac{2}{\omega^2+1} + \pi[\delta(\omega+1)+\delta(\omega-1)] \]

改编自课本 5.1.7

习题 ¶

4.21¶

设 $\{B(t);\, t \geq 0\}$ 是标准布朗运动，求：

(1) $P\{B(3.6) \leq 1 \mid B(1.6) = 0.8,\, B(2.39) = -0.1\}$；

由布朗运动的独立增量性质，有

\[ \begin{align*} &P\{B(3.6) \leq 1 \mid B(1.6) = 0.8,\, B(2.39) = -0.1\} \\ &= P\{B(3.6) - B(2.39) \leq 1 - (-0.1)\} \\ &= P\{B(3.6) - B(2.39) \leq 1.1\} \end{align*} \]

又 $B(3.6) - B(2.39) \sim N(0,\, 3.6 - 2.39 = 1.21)$，因此

\[ P\{B(3.6) - B(2.39) \leq 1.1\} = \Phi(1) \]

(2)$\operatorname{Cov}(B(8) - B(4),\, B(6))$；

\[ \begin{align*} \operatorname{Cov}(B(8) - B(4),\, B(6)) &= \operatorname{Cov}(B(8),\, B(6)) - \operatorname{Cov}(B(4),\, B(6)) \\ &= \min\{8, 6\} - \min\{4, 6\} \\ &= 6 - 4 = 2 \end{align*} \]

(3) $D(2B(1) + B(2))$。

\[ \begin{align*} D(2B(1) + B(2)) &= D(2B(1)) + D(B(2)) + 2\,\operatorname{Cov}(2B(1),\, B(2)) \\ &= 4D(B(1)) + D(B(2)) + 4\,\operatorname{Cov}(B(1),\, B(2)) \\ &= 4 \times 1 + 2 + 4 \times 1 \\ &= 10 \end{align*} \]

4.27¶

设 $\{B(t); t \geqslant 0\}$ 是标准布朗运动，计算：

(1) $P\left(B\left(\frac{1}{10}\right) \geqslant 1.5 \mid B\left(\frac{1}{6}\right) = 2,\, B\left(\frac{1}{4}\right) = 2.4\right)$；

由布朗运动的自相似性，令 $\widetilde{B}(t) = 12 B\left(\frac{t}{12}\right)$，则有

\[ \begin{align*} &P\left(B\left(\frac{1}{10}\right) \geqslant 1.5 \mid B\left(\frac{1}{6}\right) = 2,\, B\left(\frac{1}{4}\right) = 2.4\right) \\ &= P\left(\widetilde{B}(10) \geqslant 15 \mid \widetilde{B}(6) = 12,\, \widetilde{B}(4) = 9.6\right) \\ &= P\left(\widetilde{B}(10) - \widetilde{B}(6) \geqslant 3\right) \\ &= 1 - \Phi(1.5) \end{align*} \]

(2) 在 $B\left(\frac{1}{6}\right) = 2,\, B\left(\frac{1}{4}\right) = 2.4$ 的条件下，求 $B\left(\frac{1}{10}\right)$ 的条件分布。

因为自相似性，我们要求条件分布，即求 $F(B(\frac{1}{10})\leq x| B(\frac{1}{6})=2, B(\frac{1}{4})=2.4)$

根据自相似性，已知，$\widetilde{B}(6)=12$，$\widetilde{B(4)}=9.6$

又因为 Markov 性质，不需要管 $\widetilde{B}(4)$，所以

\[ \widetilde{B}(10)=\widetilde{B}(10)-\widetilde{B}(6)+12\thicksim N(12,4) \]

所以，这里构造的时候，要构造差值，要注意加上常数会改变均值

最后使用自相似性质

\[ B(\frac{1}{10})\sim\frac{1}{10}\widetilde{B(10)}\sim N(\frac{6}{5},\frac{1}{25}) \]

4.29¶

设 $\{B(t); t \geqslant 0\}$ 是标准布朗运动，对任意 $t>0, x>0$

(1) $P(|B(t)| \leqslant x)$；

解

\[ \begin{align*} P(|B(t)| \leqslant x) &= P(-x \leqslant B(t) \leqslant x) \\ &= 2\Phi\left(\frac{x}{\sqrt{t}}\right) - 1 \end{align*} \]

(2) $P\left(\max_{0 \leqslant s \leqslant t} B(s) - B(t) \leqslant x\right)$

解

\[ \begin{align*} &P\left(\max_{0 \leqslant s \leqslant t} B(s) - B(t) \leqslant x\right) \\ &= P\left(\max_{0 \leqslant s \leqslant t} (B(s) - B(t)) \leqslant x\right) \quad \text{（换元，令 $u = t - s$）} \\ &= P\left(\max_{0 \leqslant u \leqslant t} B(u) \leqslant x\right) = 1 - P\left(\max_{0 \leqslant u \leqslant t} B(u) \geqslant x\right) \\ &= 1 - 2P(B(t) > x) \\ &= 1 - 2\left[1 - \Phi\left(\frac{x}{\sqrt{t}}\right)\right] = 2\Phi\left(\frac{x}{\sqrt{t}}\right) - 1 \end{align*} \]

表达式	含义
\(P(\max_{s\leq t} B(s) \geq a)\)	布朗运动在 \([0,t]\) 曾超过 a 的概率
\(P(T_a \leq t)\)	首次达到 \(a\) 的时间早于 \(t\) 的概率
\(2P(B(t) \geq a)\)	利用布朗运动对称性 + 反射原理的结果

04 | 布朗运动 ¶

Cheet Sheet¶

定义 ¶

标准布朗运动的性质 ¶

布朗运动判定 ¶

Markov 性 ¶

自相似性 ¶

0 与 \(\infty\) 对称性 ¶

首次击中时 ¶

布朗桥运动 ¶

例题 ¶

相似性 ¶

首次击中时 ¶

布朗桥 ¶

数字特征求解与特殊 ¶

习题 ¶

4.21¶

4.27¶

4.29¶