02 | Linear Regression¶

OLS - 优化视角 ¶

考虑经典的线性回归模型：

其中：

• \(y \in \mathbb{R}^n\)：响应变量
• \(X \in \mathbb{R}^{n \times p}\)：满秩设计矩阵（列满秩）
• \(\beta \in \mathbb{R}^p\)：未知回归系数
• \(\varepsilon\)：独立同分布噪声，均值 0，方差 \(\sigma^2\)

残差平方和（Residual Sum of Squares, RSS）定义为：

也可以写成向量形式：

最小二乘估计（Ordinary Least Squares, OLS）就是选择使 RSS 最小的 \(\boldsymbol{\beta}\)：

• To estimate \(\beta\), we set the derivative equal to 0 \(\(\frac{\partial \text{RSS}}{\partial \beta} = -2 \mathbf{X}^\top (\mathbf{y} - \mathbf{X} \beta) = 0\)\)

• \(\mathbf{X}\) full rank \(\iff \mathbf{X}^\top \mathbf{X}\) invertible

性质 ¶

无偏

我们计算 \(\mathbb{E}[\hat{\beta}]\)：

方差

将 \(\mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}\) 代入：

有

UMVUE

Lehmann–Scheffé 定理告诉我们：

若某无偏估计量是充分统计量的函数，则它是 UMVUE。

我们来验证：

1️⃣ \(\hat{\beta}\) 是 \(\beta\) 的无偏估计量 → ✅

已证

2️⃣ \(X^T y\) 是充分统计量 → ✅

由因子分解定理：

• \(y \sim \mathcal{N}(X\beta, \sigma^2 I)\)
• 联合密度函数可以写成关于 \(X^T y\) 的函数和不含 \(\beta\) 的函数之积
• 所以 \(X^T y\) 是 \(\beta\) 的充分统计量

而 \(\hat{\beta}\) 是 \(X^T y\) 的函数 ⇒ 它是充分统计量的函数

✅ 满足 Lehmann–Scheffé 定理条件 ⇒ 是 UMVUE！

或者你也可以使用 Gauss-Markov 定理（非正态条件下）

但要注意：

• Gauss-Markov 定理 → 最优线性无偏估计（BLUE）
• Lehmann–Scheffé 定理（+ 正态性）→ 最小方差无偏估计（UMVUE）

Training Error & Test Error¶

OLS - 统计视角 ¶

首先定义拟合误差 :

其中假设噪声 \(e\) 服从白噪声高斯分布

使用高斯噪声的建模假设：模型的预测能力是比较好的，没有 outlier（超出 \(3\sigma\) 的离群值），比如上课一次不来，作业一次不交，考试考 100 分的样本

在这种时候使用高斯噪声建模，可以得到一个比较好的结果

因此条件概率可以写作 :

根据极大似然估计 , 我们需要找到一个 \(z\) 使得 \(p(b|Az)\) 最大 :

conditional pdf 对 b

likelihood function 对 z

DLS - 最小数据二乘 ¶

假设数据矩阵 \(A\) 存在误差（比如记录样本数据的时候写错了）

使用校正量 \(\Delta A\) 来表示误差 , 即考察下面的约束优化问题

underlying idea: 每个数据的误差不会特别大

对于有约束问题，写出拉格朗日函数

求导数并令导数为 0

可以解出

把 \(\Delta A\) 和 \(\lambda\) 代入 \(L(A, \lambda)\)，得到

变成了一个无约束的优化问题

• 方法 1: 使用梯度下降法求解 \(x^{t+1} = x^t - \eta \nabla J(x^t)\)
• 方法 2: 这是一个分式优化的问题 (Fractional Programming)，2018 IEEE TSP

• Fix \(x\), 那么 \(y\) 有闭式解
• Fix \(y\), 那么 \(x\) 是凸优化问题

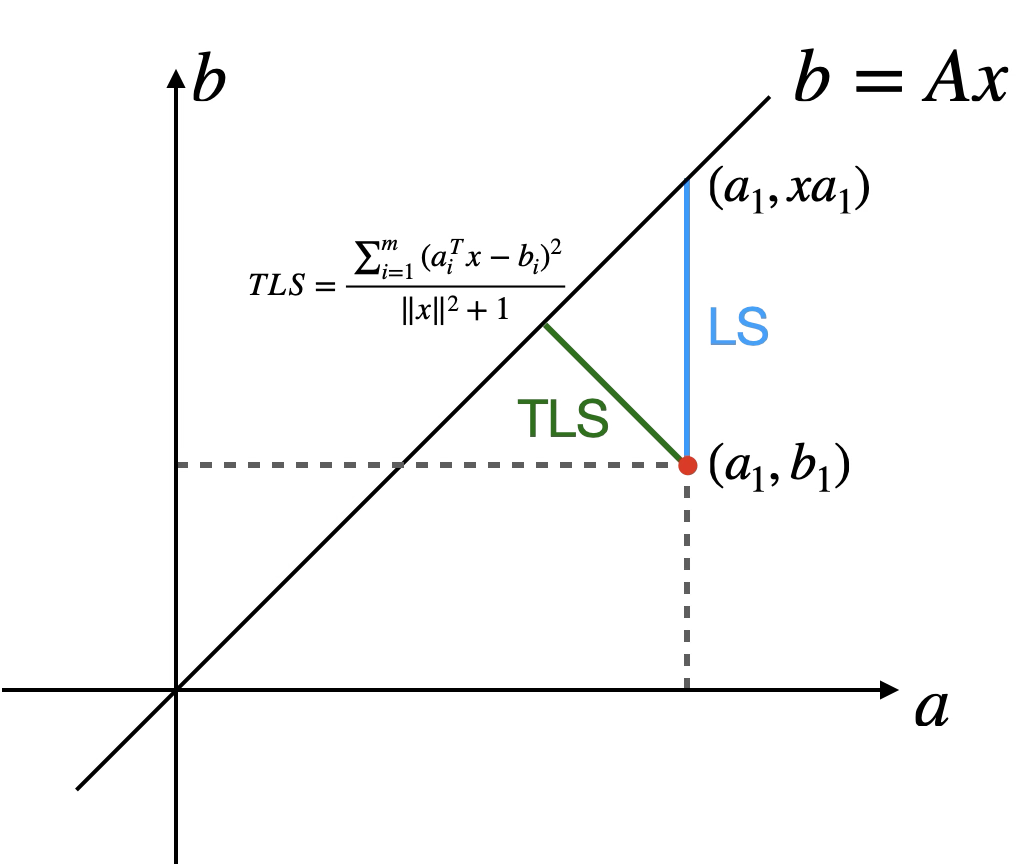
TLS - 总体最小二乘 ¶

优化问题：纠正最小 \(\Delta A\) 和 \(\Delta b\)，同时可以满足约束

步骤 ¶

1. input \(A\) 和 \(b\)
2. 增广矩阵 \(B = \begin{bmatrix} A & b \end{bmatrix}\)
3. \(B^HB = V \Sigma V^H\)
4. 找 \(\lambda_{min}\) 对应的特征向量 \(v_{min}\)
5. \(z^{\star} = v_{min} \times \frac{-1}{v_ {n+1}}\)

问题求解 ¶

写成分块矩阵的形式

令

所以原始问题可以写成

可以看出，TLS 是 DLS 在 \(b = 0\) 的特殊情况

使用拉格朗日乘子法

两个二次型相除：Rayleigh 商，有闭式解（在 PCA 和 TLS 中都有应用）

对 \(B^HB = V \Sigma V^H\) 进行特征值分解

那么最优解 \(z^{\star} = \begin{bmatrix} x^{\star} \\ -1 \end{bmatrix} = v_{min}\)（最小特征值对应的特征向量）

但是这里存在一个问题：\(v_{min}\) 的最后一行不一定是 \(-1\), 所以需要进行归一化，把最后一行构造成 \(-1\)

几何含义 ¶

普通 LS 是让竖直方向的距离误差最小

而 TLS 是让垂直方向上的距离误差最小 ; 即找到一条直线，让所有点到直线的距离最小

对于直线 \(Ax -b = 0\)，如果我们把 \(A\) 看作是横坐标变量，\(b\) 看作是纵坐标变量，那么点 \((a_1,b_1)\) 到直线 \(b = Ax\) 的距离就是

广义线性回归 ¶

logistic¶

线性回归有一个很强的假设，就是 y 是连续的；并且有更像邻近数的趋势 (MSE 对于线性回归不是一个好的 function)

• one vs. Rest

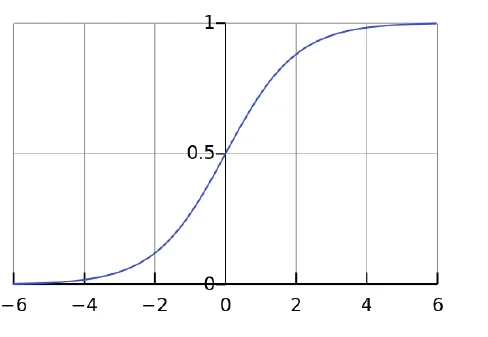
logistic function:

• sigmoid function: \(f(x) = \frac{1}{1+e^{-x}}\) CDF(累积分布函数)ofthe standard logistic distribution
  使用sigmoid函数将线性回归的输出转换为概率

为什么 loss function 要取 log - 为了方便求导 - 取log使得连乘变成连加，不会丢失信息

Assumptions behind logistic regression - l(a) = -sum_{iin I} log(1+e^{-y_i a^T x_i})

pros: - binomial distribution is a good assumption for classification - provide a probability - low computation, easy to optimize - support online learning:梯度下降的模型都支持在线学习

cons: - too simple:high bias & low variance

对于分类问题，只关心分类正确的类的值

Penalty¶

A unified framework is to minimize the objective function

where \(P_{\lambda}(\cdot)\) is a penalty function applied on the value of each parameter, and \(\lambda\) is a tuning parameter.

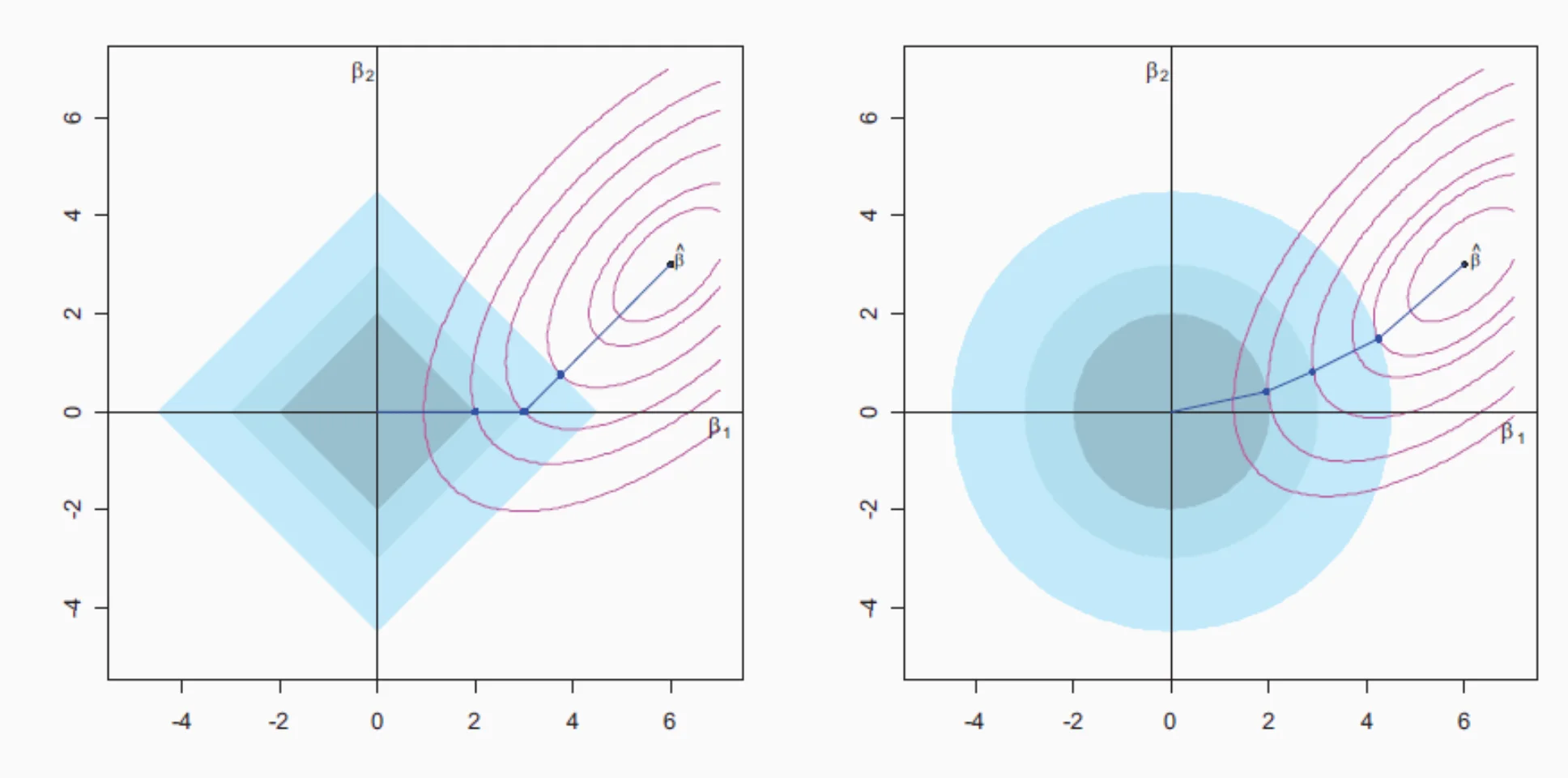
• Lasso: \(P_{\lambda}(\beta) = \lambda|\beta|\)
• Ridge: \(P_{\lambda}(\beta) = \lambda\beta^2\)
• Best subset: \(P_{\lambda}(\beta) = \lambda\mathbf{1}\{\beta \neq 0\}\)
• Elastic net: \(P_{\lambda}(\beta) = \lambda_1|\beta| + \lambda_2\beta^2\)

Lasso - l1¶

求解下面的优化问题

• Each value of \(\lambda\) corresponds to an unique value of \(s\).

Lasso 回归在正交设计下的推导与原理 ¶

假设：

• 设计矩阵满足 \(\mathbf{X}^\top \mathbf{X} = \mathbf{I}_p\)（即列向量正交，单位范数）
• 目标是求解 Lasso 回归问题：

步骤 1：插入 OLS 解

因为 OLS 解为：

我们将其插入目标函数：

其中最后一项为 0 是因为：

• 残差 \(\mathbf{r} = \mathbf{y} - \mathbf{X} \widehat{\boldsymbol{\beta}}^{\text{ols}}\) 垂直于 \(\operatorname{Col}(\mathbf{X})\)
• 而 \(\mathbf{X}(\widehat{\boldsymbol{\beta}}^{\text{ols}} - \boldsymbol{\beta}) \in \operatorname{Col}(\mathbf{X})\)

步骤 2：目标函数化简

因为第一项与 \(\boldsymbol{\beta}\) 无关，我们只需最小化第二项 + 正则项：

变量独立求解

目标函数可分解为每个参数的独立优化：

这就是经典的 Soft Thresholding 问题，解为：

即：

• 如果 \(|a| \leq \lambda/2\)，解为 0
• 否则，在方向上缩减 \(\lambda/2\)

Soft Thresholding = 变量选择机制

• Ridge 回归使用 \(\ell_2\) 惩罚：系数永远不会变为 0，只是变小
• Lasso 使用 \(\ell_1\) 惩罚：会直接把小的系数压成 0
• 所以 Lasso 能实现 变量选择（sparsity）

Ridge - l2¶

优化视角 ¶

最优化视角，即求解下面的最优化问题

Take derivative with respect to \(\beta\) and set to zero

PCA 视角 ¶

将协方差矩阵写成 PCA 形式：

• 说明协方差的主方向（特征向量）就是 \(V\)，对应特征值 \(d_j^2\)
• 第 \(j\) 个主成分为 \(X v_j = d_j u_j\)
• 大的奇异值方向：数据方差大，保留信息多
• 小的奇异值方向：容易过拟合，要强烈惩罚

Ridge 回归对响应变量的估计：

1. 把 \(\mathbf{y}\) 投影到每个主成分方向 \(u_j\)
2. 投影结果 \(u_j^\top y\) 被 缩小 了一个因子 \(\frac{d_j^2}{d_j^2 + \lambda}\)
3. \(d_j^2\) 小的方向（低方差）被惩罚得更严重，防止对噪声过拟合

贝叶斯视角 ¶

📌 先验假设

我们将回归系数 \(\boldsymbol{\beta}\) 视为一个随机变量，赋予如下先验分布：

这是一个零均值、高斯先验，对每个参数都做了 \(\ell_2\) 范数的惩罚。

🎯 似然函数（来自线性模型）

🧠 后验分布

利用贝叶斯定理（高斯 + 高斯 ⇒ 高斯），得到后验分布为：

其中后验 均值 正是 Ridge 回归的解析解：

Tikhonov 正则化 ¶

对于 OLS 问题，我们求解

但是如果 \(A\) 是病态的，那么 \((A^T A)^{-1}\) 会很大，导致 \(x_{LS}\) 不稳定

很直观的想法是让 \(A^{H}A\) 变得好一些，即

(Bayesian Linear Regression)

Tikhonov 证明求下面的优化问题和上面的等价

• 解决过拟合
• 解决病态问题，提高数值稳定性

• 代价函数对应的是 likelihood
• 正则项对应的是 prior

bias¶

Ridge 回归是有偏估计

• 因为 \(Z \neq I\)，所以 ridge 估计是 有偏的
• 随着正则化参数 \(\lambda\) 增大，bias² 增加
• 这是偏差 - 方差权衡的一部分

variance¶

自由度 ¶

• Ridge 回归虽然估计 \(\widehat{\boldsymbol{\beta}}^{\text{ridge}} \in \mathbb{R}^p\)，但由于 Shrinkage，不等价于使用所有 \(p\) 个变量的全部自由度。

• 自由度随着 \(\lambda\) 的变化而变化：

  • \(\lambda \to 0\): Ridge 退化为 OLS，\(\text{df} = p\)
  • \(\lambda \to \infty\): 所有参数被压缩到 0，\(\text{df} \to 0\)

  • 所以：

    \[ 0 \leq \text{df}(\lambda) \leq p \]

• 若对 \(\mathbf{X}\) 做奇异值分解（SVD）：

  \[ \mathbf{X} = UDV^\top, \quad \text{其中} \ D = \operatorname{diag}(d_1, \dots, d_p) \]

• 则自由度可写为：

• 每个主成分方向 \(j\) 的自由度贡献是一个 shrinkage 因子：

  $$ frac{d_j^2}{d_j2 + lambda} $$ * 方差小的方向（\(d_j\) 小）会被严重 shrink，自由度贡献也少 * 这是 Ridge 比 OLS 更稳健但有偏的原因

elastic¶

lasso 与 ridge 对比 - Ridge is \(\ell_{2}\) penalty - Lasso is \(\ell_{1}\) penalty - Best subset is \(\ell_{0}\) penalty - Bridge penalty is \(\ell_{q}\) normal

\(q = 4\)
\(q = 2\)
\(q = 1\)
\(q = 0.5\)
\(q = 0.1\)

\(\sum_{j}|\beta_{j}|^{q}\) for given values of \(q\).

Elastic-net is a hybrid of \(\ell_{1}\) and \(\ell_{2}\):

\(\lambda_{1}\|\beta\|_{1} + \lambda_{2}\|\beta\|_{2}^{2}\)

LDA¶

理解主成分分析（1）——最大方差投影与数据重建 - Fenrier Lab

简单理解线性判别分析 - 知乎

LDA 线性判别分析——投影的疑问解答 _lda 投影 -CSDN 博客

最小化类内方差

最大化类间方差

因为自变量只有 \(w\)，不一定二者都能同时达到最优，所以整合到一起取下式的最大值：

LDA——线性判别分析基本推导与实验 -CSDN 博客

二分类线性判别分析，看懂这篇就够了 - 知乎