04 | 有约束 解析解法
2436 9 张图片 10
Dual Ascent Method
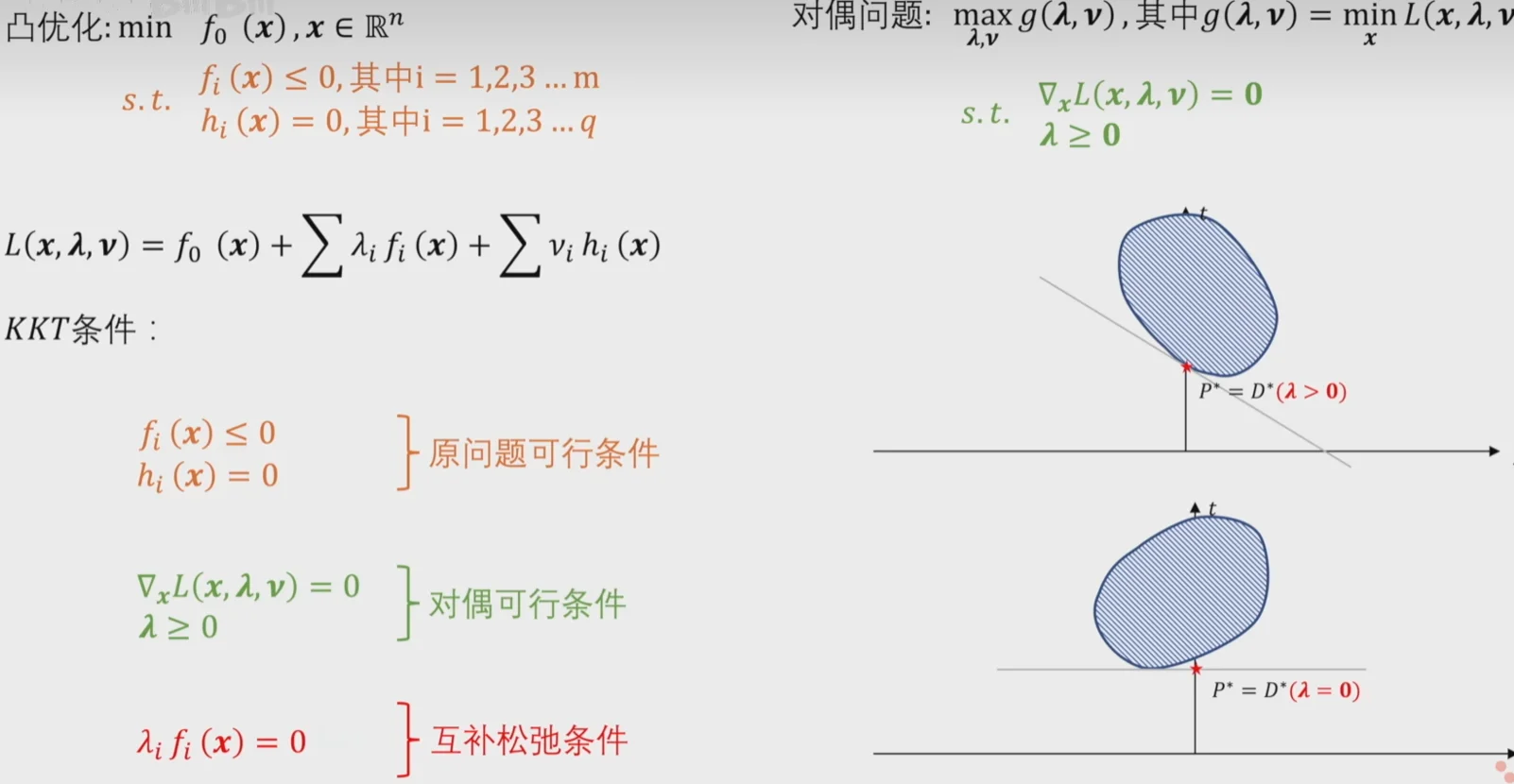
拉格朗日函数把约束问题转化为无约束问题
Fix \(\lambda,v\) ,update \(x_k\) :
\[
x_{k+1} = \arg \min_{x} L(x, \lambda_k, v_k)
\]
Fix \(x_{k+1}\) ,update \(\lambda,v\) :
\[
\lambda_{k+1},v_{k+1} = \arg \max_{\lambda,v} L(x_{k+1}, \lambda, v)
\]
we tweak the dual variables to improve the balance iteratively aimly to set as close as possible to the best solution that respects all of the constraints
有点像 fine-tuning
\[
\begin{array}{ll}
\min & f(x) \\
\text{s.t.} & h_i(x) = 0, \quad i = 1, 2, ..., m \\
& x \in \mathbb{R}^n
\end{array}
\]
拉格朗日函数
\[
L(x, \lambda) = f(x) + \lambda^T h(x) = f(x) + \sum_{i=1}^m \lambda_i h_i(x)
\]
其中,\(\lambda = [\lambda_1, \lambda_2, ..., \lambda_m]^T\) 。
对 \(L(x, \lambda)\) 0
\[
\frac{\partial L(x, \lambda)}{\partial x} \Big|_{x^*} = 0 \quad \Rightarrow \quad \nabla f(x^*) + \sum_{i=1}^m \lambda_i \nabla h_i(x^*) = 0
\]
\[
\frac{\partial L(x, \lambda)}{\partial \lambda} \Big|_{x^*} = 0 \quad \Rightarrow \quad h_i(x^*) = 0, \quad i = 1, 2, ..., m
\]
只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为 0
不等式约束
\[
\begin{array}{ll}
\min & f(x) \\
\text{s.t.} & g_i(x) \geq 0, \quad i = 1, 2, ..., m \\
& x \in \mathbb{R}^n
\end{array}
\]
可行方向判别条件(充分条件) 对于点 \(x^{(0)}\) \(p\) \(x^{(0)}\)
\[
\nabla g_j(x^{(0)})^T p \geq 0, \quad \forall j \in J(x^{(0)})
\]
其中,\(J(x^{(0)}) = \{j \mid g_j(x^{(0)}) = 0, j = 1, 2, ..., l\}\)
证明:根据 Taylor
\[
g_j(x^{(0)} + \lambda p) = g_j(x^{(0)}) + \lambda \nabla g_j(x^{(0)})^T p + O(\lambda)
\]
当 \(\lambda\) \(j \in J(x^{(0)})\) \(g_j(x)\)
\[
g_j(x^{(0)} + \lambda p) \geq 0
\]
如果 \(j \in J(x^{(0)})\) \(\nabla g_j(x^{(0)})^T p > 0\)
\[
g_j(x^{(0)} + \lambda p) \geq 0
\]
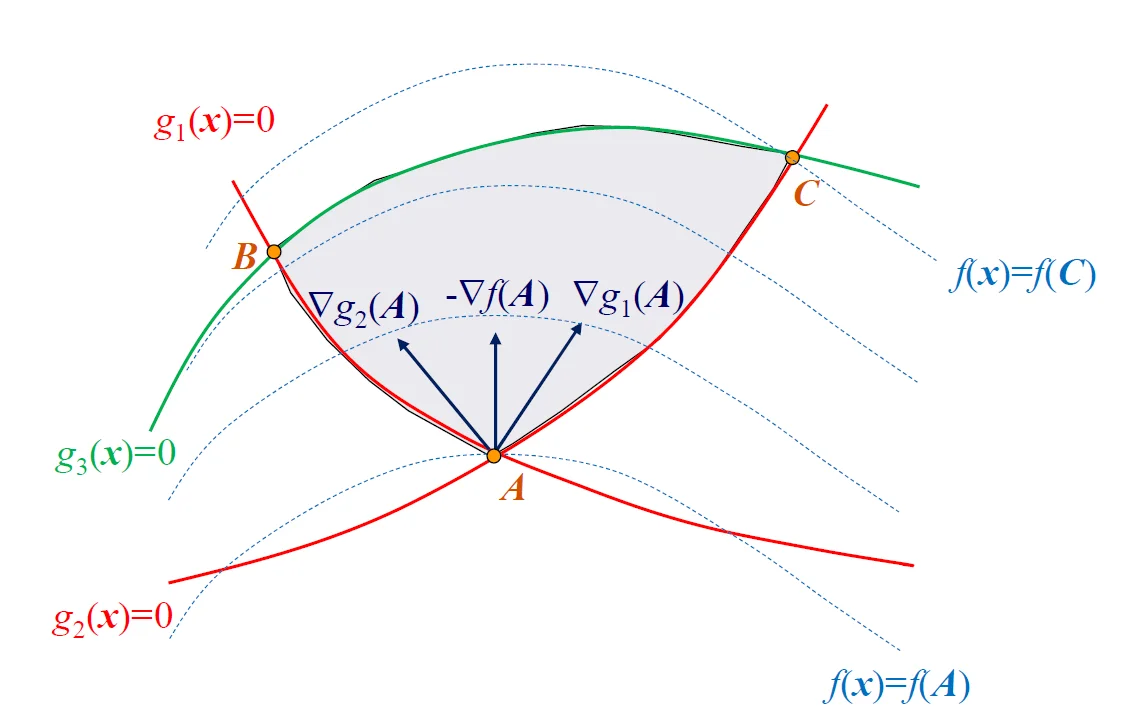
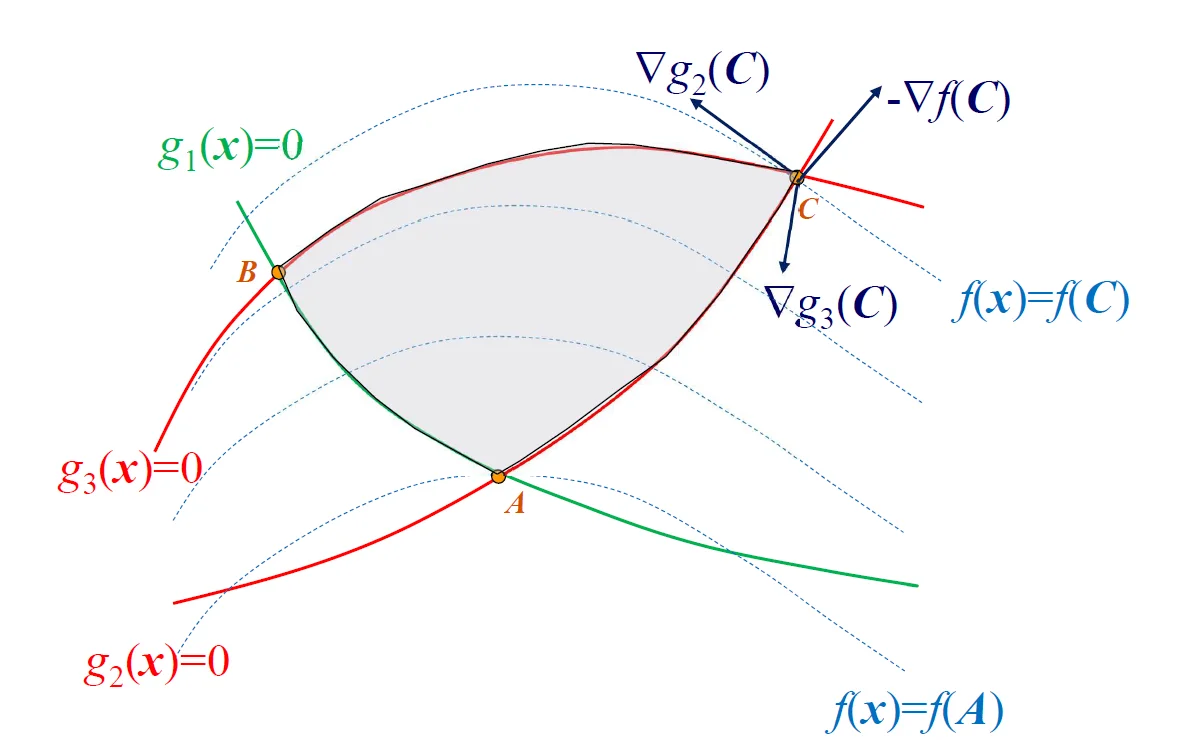
几何含义:与所有起作用约束梯度的夹角小于 \(90^\circ\)
局部极小值存在的直观条件
在点 \(x^*\)
\[
\nabla f(x^*)^T p < 0
\]
\[
\nabla g_j(x^*)^T p > 0, \quad j \in J(x^*)
\]
其中,\(J(x^*)\)
几何含义:不存在与 \(\nabla f(x^*)\) \(\nabla g_{j \in J(x^*)}\)
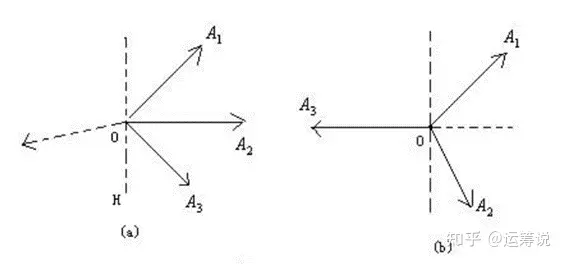
Gordan 引理设 \(B \in R^{m\times n}\) \(Bx < 0\) \(B^T y = 0, y \ge 0, y \ne 0\)
参考网址:运筹说 第 99 | 凸集分离定理中的 Gordan “拉格朗日对偶问题”如何直观理解? “KKT 条件” “Slater 条件” “凸优化”打包理解 _ _bilibili
翻译一下:\(B^T\) 是\(R^n\) 中一组基,由\(m\) 个\(n\) 维列向量组成,只存在两种情况:
存在一个方向,与 \(B^T\)
\(B^T\) 如果一组基的非负组合是一个凸锥,则等价为这组基的正组合表示不了原点,除非系数都是 0 \(b_j\)
正线性相关(positive linear dependence)
几何含义:\(a_j\)
正线性相关 \(\Rightarrow\)
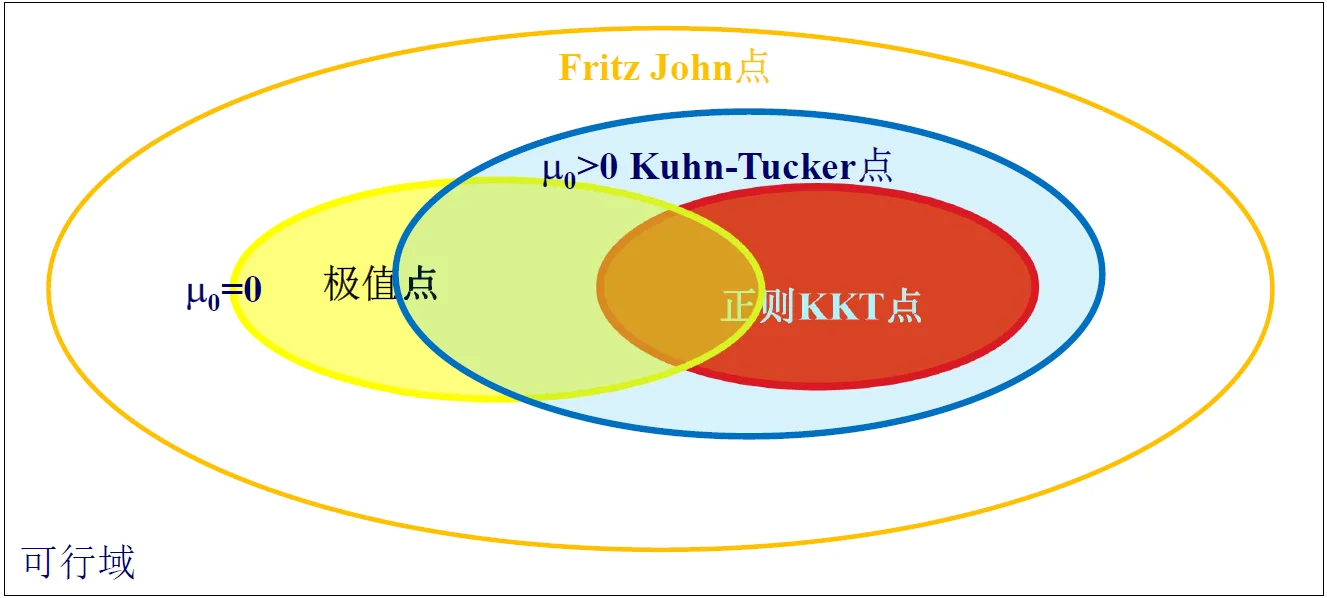
Fritz John 定理\[
\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \mu_i^* \nabla h_i(x^*) + \sum_{i=1}^m \mu_i^{**} \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
\]
\[
\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m (\mu_i^* - \mu_i^{**}) \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
\]
\[
\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
\]
其中,\(\gamma_i = \mu_i^* - \mu_i^{**}\) ,并且有:
\[
\mu_i^* \ge 0 \quad \mu_i^{**} \ge 0 \quad \Longrightarrow \gamma_i = \mu_i^* - \mu_i^{**} \text{ 无符号约束 } \quad i = 1, 2, ..., p
\]
注意,\(\mu_0\) 、\(\mu_j\) 、\(\gamma_i\) 不可同时为 0
\(\gamma_i\)
假设 \(x^*\) \(\mu_j^* (j=0, 1, 2, ..., m)\) \(\gamma_i (i=0, 1, 2, ..., p)\)
\[
\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0 \quad 拉格朗日条件
\]
\[
\mu_j^* g_j(x^*) = 0 \quad j = 1, 2, ..., m \quad 互补松弛条件\\
\gamma_i h_i(x^*) = 0 \quad i = 1, 2, ..., p \quad 等式互补松弛
\]
\[
\mu_j^* \ge 0 \quad j = 0, 1, ..., m\\
\sum_{j=0}^l \mu_j^* + \sum_{i=1}^m |\gamma_i^* |\neq 0 \quad 强非负条件
\]
对于紧致的约束条件,\(g(x^*) = 0\) ,但是 \(\sum_{j=1}^l \mu_j \nabla g_j(X^*)\) \(\lambda_i \neq 0\)
对于松弛的约束条件,将 \(x^*\) 0 的,最重要的是要让梯度在 \(\lambda_i\) \(\lambda_i>0\) \(\lambda_i=0\)
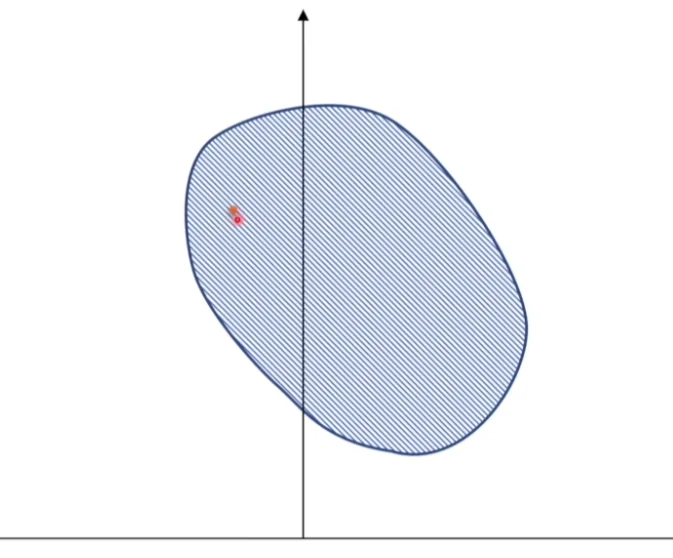
Slater 条件——强对偶的充分条件Slater 条件是指:存在一个点 \(x \in relint D\) \(relint D\) \(D\)
使得 \(f_i(x) < 0\) \(i = 1, 2, 3, ..., m\) \(Ax = b\) 。
换句话说,Slater 条件是指在可行域的内部存在一个点,使得所有约束函数的值都小于零。这个条件在线性规划和非线性规划中都有应用,是判断对偶问题是否具有强对偶性的充分条件之一 。
内部存在点
KKT 条件——强对偶的必要条件正则条件(regular condition)是指起作用约束 \(\nabla g_{i^*}(x^*)\)
性质:若极小值 \(x^*\) KKT \(x^*\) Fritz John 条件中的 \(\mu_i>0\)
Kuhn-Tucker 定理:若 \(x^*\) ) ,则 Kuhn-Tucker
对于问题来说
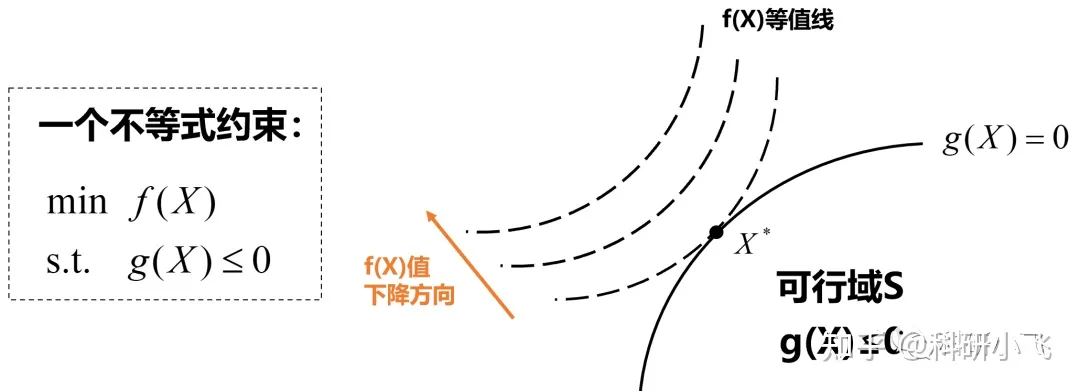
\(min f(x) \\s.t. \quad g(X) \le 0\)
求得 \(X^*\)
\(g(X^*) <0\) \(\lambda =0\) \(g(X^*) = 0\) \(\lambda \ge 0\) \(g(X^*) > 0\)
那如果想要不分类讨论 \(\lambda g(X^*) = 0\)
!!! note "能解出最优解的一定是等式,故式 (1)(2)(3)
式 (4) (5) "
(1)如果目标为最小化(Min)问题,那么不等式约束需要整理成“\(\le0\) ”的形式;
(2)如果目标为最大化(Max)问题,那么不等式约束需要整理成“\(\ge0\) ”的形式;
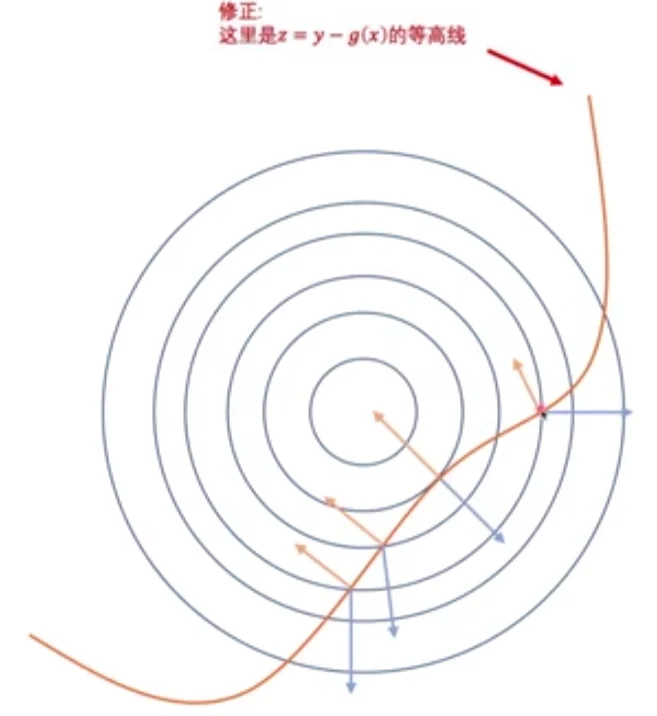
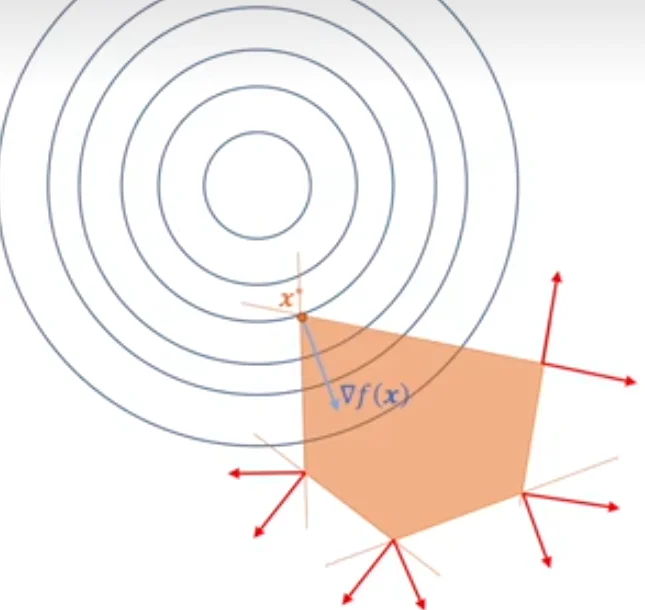
梯度方向垂直于函数等值线,指向函数值增长的方向。
(2)画出 f(X) ) :
梯度方向是函数值增长的方向,因此指向右下方;负梯度方向是函数值下降的方向,指向左上方;
(3)画出 g(X) 的梯度方向(下图蓝色方向):
由于曲线是 g(X)=0,右下方是 g(X)<0,是在下降,因此,g(X) 函数值增长的方向就是左上方了。
在最优解 X处, f(X*) 和 g(X*) 共线且方向相反。 向量共线且方向相反 * 在数学上的写法就是:
负梯度向量是另一个梯度向量的 \(lambda\) 。移项后发现,这不就是KKT 条件的第一个等式) +lambda nabla g(X^ ) = 0, lambda ge 0
end{align}
$$
KKT 条件的矩阵形式\[
\begin{align}
y^* =
\begin{bmatrix}
y_1^* \\
y_2^* \\
\vdots \\
y_m^*
\end{bmatrix}\\
\end{align}
\]
\[
\nabla h(x) =
\begin{bmatrix}
\nabla h_1(x) & \nabla h_2(x) & \cdots & \nabla h_m(x)
\end{bmatrix}
\]
\[
\nabla g(x) =
\begin{bmatrix}
\nabla g_1(x) & \nabla g_2(x) & \cdots & \nabla g_l(x)
\end{bmatrix}=
\begin{bmatrix}
\frac{\partial g_1}{\partial x_1} & \frac{\partial g_2}{\partial x_1} & \cdots & \frac{\partial g_l}{\partial x_1} \\
\frac{\partial g_1}{\partial x_2} & \frac{\partial g_2}{\partial x_2} & \cdots & \frac{\partial g_l}{\partial x_2} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial g_1}{\partial x_n} & \frac{\partial g_2}{\partial x_n} & \cdots & \frac{\partial g_l}{\partial x_n}
\end{bmatrix}^T
\]
Lagrange 驻点条件
\[
\nabla f(x^*) - \nabla h(x^*)y^* - \nabla g(x^*)\mu^* = 0
\]
互补松弛条件
\[
\mu^* \odot g(x^*) = 0 \\\Leftrightarrow \mu_j^* g_j(x^*) = 0 \quad j=1,2,...,l
\]
非负条件
\[
\mu^* \geq 0
\]
可行性条件
\[
\begin{aligned}
h(x^*) &= 0 \\
g(x^*) &\geq 0
\end{aligned}
\]
例题
\[
\min f(x_1, x_2) = (x_1 - 2)^2 + x_2^2 \\
s.t.
\left\{
\begin{array}{lr}
x_2 \le x_1 + 2 \\
x_2 \ge x_1^2 + 1 \\
x_1 \ge 0 \quad x_2 \ge 0
\end{array}
\right.
\]
列出向量
\[
\begin{align}
f(\mathbf{x}) = (x_1 - 2)^2 + x_2^2
\end{align}
\]
\[
\nabla f(\mathbf{x}) = \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right]
\]
\[
\mathbf{g}(\mathbf{x}) = \left[ \begin{array}{c} x_1 - x_2 + 2 \\ -x_1^2 + x_2 - 1 \\ x_1 \\ x_2 \end{array} \right]
\]
\[
\nabla \mathbf{g}(\mathbf{x}) = \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right]
\]
列出题目条件
\[
\begin{align*}
\nabla f(x^*) - \nabla h(x^*) y^* - \nabla g(x^*) \mu^* = 0
\end{align*}
\]
\[
\Longrightarrow \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right] - \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \mu_1 \\ \mu_2 \\ \mu_3 \\ \mu_4 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
\]
\[
\mu^* \otimes g(x^*) = 0 \quad \Longrightarrow \left[ \begin{array}{c} \mu_1 (x_1 - x_2 + 2) \\ \mu_2 (-x_1^2 + x_2 - 1) \\ \mu_3 x_1 \\ \mu_4 x_2 \end{array} \right] = 0
\]
\[
g(x^*) \ge 0 \quad \mu^* \ge 0
\]
得出方程
\[
\begin{align*}
2(x_1 - 2) - \mu_1 + 2 \mu_2 x_1 - \mu_3 = 0 \\
2x_2 + \mu_1 - \mu_2 - \mu_4 = 0 \\
\mu_1 (x_1 - x_2 + 2) = 0 \\
\mu_2 (-x_1^2 + x_2 - 1) = 0 \\
\mu_3 x_1 = 0 \\
\mu_4 x_2 = 0 \\
\mu_j \ge 0 \quad j = 1, 2, 3, 4 \\
x_2 \le x_1 + 2 \\
x_2 \ge x_1^2 + 1 \\
x_1, x_2 \ge 0
\end{align*}
\]
求解方程
观察可得:\(\mu_1 = \mu_3 = \mu_4 = 0\) (松弛性)
所以有:
\[
(1 + \mu_2) x_1 - 2 = 0
\]
\[
2x_2 - \mu_2 = 0
\]
\[
-x_1^2 + x_2 - 1 = 0
\]
求解得:
\[
\mu_2^* = 2.6219 \quad x_1^* = 0.5536 \quad x_2^* = 1.3064
\]
\[
f(x^*) = 3.7989
\]
条件与分析
KKT 条件是判断某点是极值点的必要条件 ,不是充分条件 。换句话说,最优解一定满足 KKT ,但KKT 条件的解不一定是最优解
对于凸规划 ,KKT 条件就是充要条件 了,只要满足 KKT 全局最优解 。