01 | 定义与数学建模
约 1308 个字 5 张图片 预计阅读时间 5 分钟
随想
这部分的几节课数学推导比较多,但是基本思想不是特别难。
使用到的主要是多元函数求导、偏导、极值、二次型等内容
凸集
定义
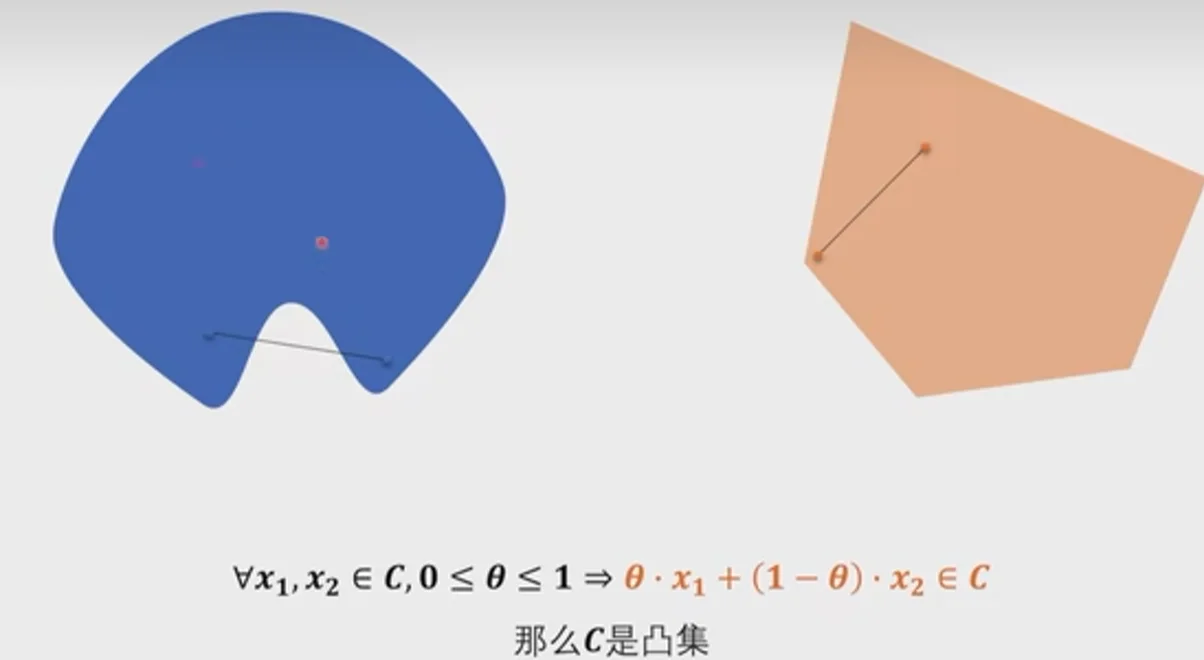
设集合 \(C \subseteq \mathbb{R}^n\),如果对于任意 \(x_1, x_2 \in C\) 和任意 \(\lambda \in [0,1]\),都有:
\[
\lambda x_1 + (1-\lambda)x_2 \in C
\]
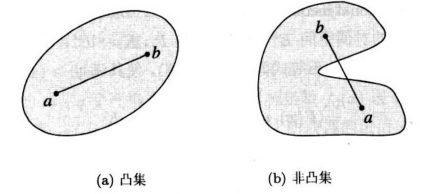
那么称集合 \(C\) 为凸集。
直观上说,凸集中任意两点的连线段都完全包含在该集合内。
性质
\[
h_{i}(x)=0 \quad g_{j}(x) \leq 0 \quad 凸集的交集为凸集
\]
- 如果最优解存在,最优解集合也为凸集,最优解的连线段均为最优解
\[
\begin{align}
f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}\right] \leq f\left(x_{1}^{*}\right)+(1-\lambda)\\ f\left(x_{2}\right)=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right) ,0<\lambda<1 \\
f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}^{*}\right]=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right)
\end{align}
\]
- 推论:线性规划问题的最优解集为所有最优顶点构成的多边形。(归纳法证)
\[
\begin{align}
x^{*}=\sum_{i=1}^{r} \alpha_{i} x^{*}_{i} \\ \sum_{i=1}^{r} \alpha_{i}=1 \\0 \le \alpha_{i} \le 1 \quad i=1, \cdots ,r
\end{align}
\]
凸函数
凸函数的定义
设函数 \(f(x)\) 在向量空间 \(\mathbb{R}^n\) 的某个凸子集 \(C\) 上有定义,如果对于任意 \(x_1, x_2 \in C\) 和任意 \(\lambda \in [0, 1]\),都有:
\[
f(\lambda x_1 + (1-\lambda) x_2) \le \lambda f(x_1) + (1-\lambda) f(x_2)
\]
那么函数 \(f(x)\) 就被称为定义在 \(C\) 上的凸函数。
这个定义意味着,对于定义域内的任意两点,函数曲线上的这两点之间的部分都在这两点的连线下方。
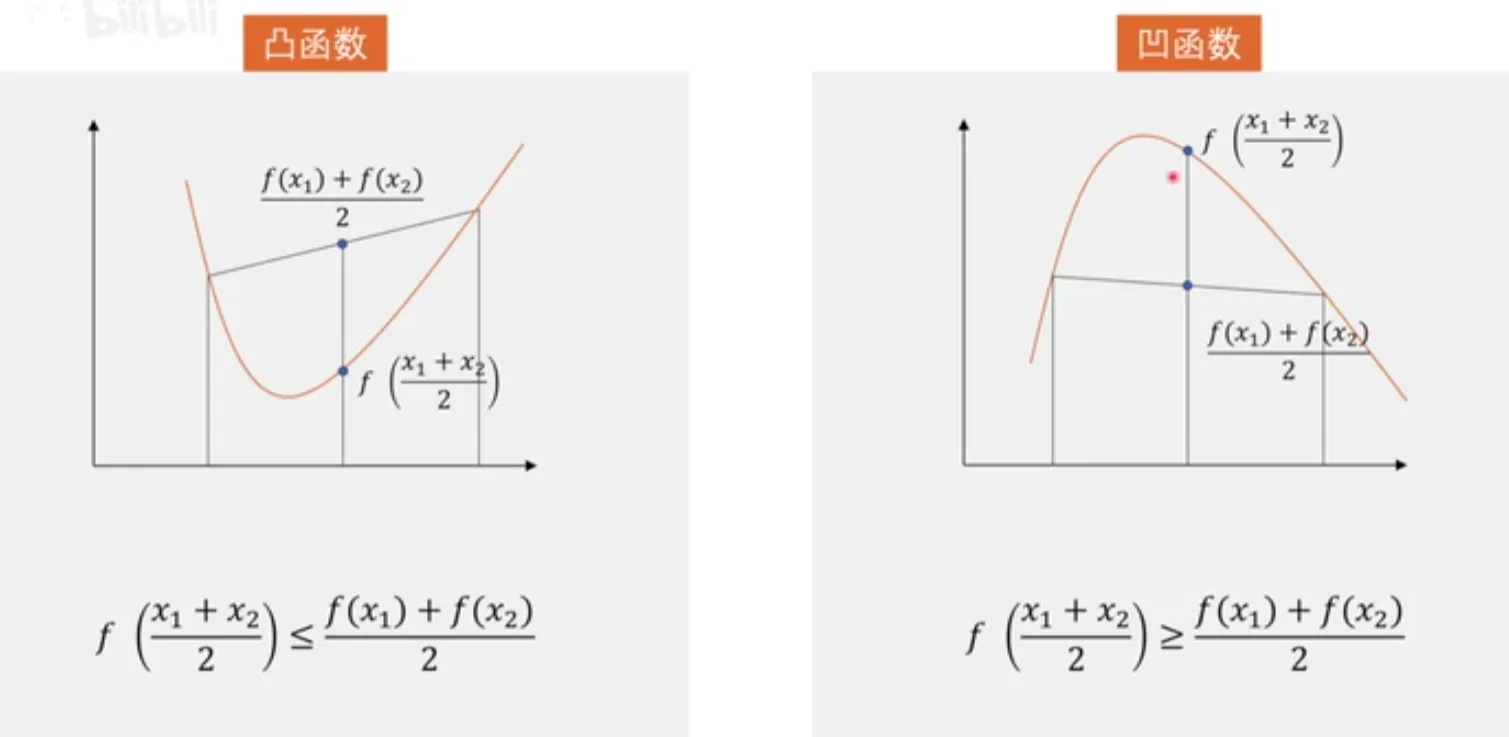
- convex function 凸函数
- concave function 凹函数
判定
一阶条件:
对于任意的 \(x_1, x_2 \in \mathbb{R}^n\),都有
\[
f(x_2) \geq f(x_1) + \nabla f(x_1)^T (x_2 - x_1)
\]
几何意义:任何一点的切线在凸函数曲线的下方。
二阶充分必要条件:
\[
H_x f(x) = \frac{\partial^2 f(x)}{\partial x \partial x^T} \succ 0,\forall x \in S
\]
即 Hessian 矩阵在整个凸集\(S\) 均正定
几何意义:函数曲线向上弯曲。
凸函数的性质
- 若 \(f(x)\) 是定义在凸集 \(\mathbb{R}^n\) 上的凸函数,则其 \(\beta\) 水平集 \(S_\beta\) 为凸集。
半平面是凸集
- 对于凸函数 \(f(x)\),若存在 \(x^* \in \mathbb{R}^n\) 满足
\[
\nabla f(x^*)^T (x - x^*) \geq 0 \quad \forall x \in \mathbb{R}^n
\]
则 \(x^*\) 为 \(f(x)\) 的全局最小点。
站在山谷底看,哪里都是向上走
- 对于凸目标函数,\(\nabla f(x^*) = 0\) 是 \(x^*\) 为极小值的充要条件。
凸优化
凸优化问题:函数是凸函数,可行域是凸集
凹函数求最大值其实是一样的,加一个负号就可以了
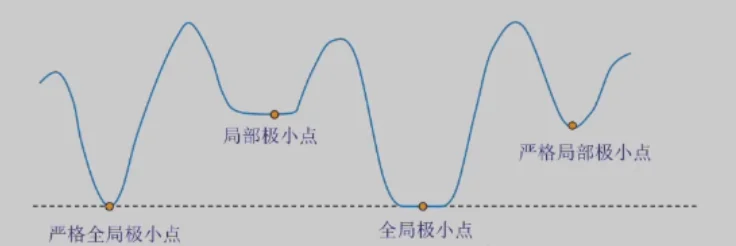
- 任何局部极值解也是全局最优解(目标函数为凸函数)最优解的唯一性为数值解法提供了方便。
-
若目标函数为严格凸函数,则如果全局最优解存在,必为唯一全局最优解。(反证法)
\[
f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}^{*}\right]<\lambda f\left(x_{1}^{*}\right)+(1-\lambda) f\left(x_{2}^{*}\right)=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right)
\]
凸优化问题
线性规划 (LP): linprog
* 混合整数线性规划 (MILP): intlinprog
二次规划 (QP): quadprog
* 二阶锥规划 (SOCP): coneprog
* 半定规划 (SDP): Yalmip 中调用 SDP 求解器
- 无约束极值问题:fminunc
- 有约束极值问题:fmincon
\[
\text { LPS } \subseteq \text { QPS } \subseteq \text { QCQPS } \subseteq \text { SOCPs } \subseteq \text { SDPs } \subseteq \text { 锥规划 } \mid \text { CPs }
\]
方法
- 松弛到更大的区域
- 分支定解法,拆解成多个凸集进行分布求解
变换方法 - 把非凸问题转换为凸问题
数学模型
\[
\begin{array}{ll}
\min_{x\in \mathbb{O}} & f(x) \\
\text{s.t.} & h_i(x) = 0, \quad i = 1, 2, ..., m \\
& g_j(x) \ge 0, \quad j = 1, 2, ..., l \\
\end{array}
\]
将等式约束变为不等式约束,可以得到
\[
\begin{array}{ll}
\mathop{min}_{x\in \mathbb{O}} & f(x) \\
\text{s.t.} & h_i(x) \ge 0, \quad i = 1, 2, ..., m \\
& -h_i(x) \ge 0, \quad i = 1, 2, ..., m \\
& g_j(x) \ge 0, \quad j = 1, 2, ..., l \\
\end{array}
\]
以求最小值为标准问题
原问题
\[
\begin{align*}
\min_x \ f_0(x), x \in \mathbb{R}^n \\
\text{s.t.} \quad f_i(x) \le 0, \text{其中} i=1,2,3...m \\
h_i(x) = 0, \text{其中} i=1,2,3...q
\end{align*}
\]
等价问题
\[
\begin{align}
\min_x \ \max_{\lambda, \nu} \ L(x, \lambda, \nu)
= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
\text{s.t.} \quad \lambda_i \ge 0 \\
\end{align}
\]
等价性的证明
\[
x 在可行域内
\left\{
\begin{array}{lr}
\lambda_i f_i(x) = 0 \quad 或 \lambda_i = 0 \quad n 或 f_i(x) = 0 \\
\nu_i h_i(x) = 0 \quad 或 \nu_i = 0 \quad 或 h_i(x) = 0
\end{array}
\right.
\]
- 当 \(x\) 在可行域内时,\(\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)\)
- 当 \(x\) 不在可行域内时,\(\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty\)
因此,\(\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)\)
对偶问题
\[
\begin{align}
\max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})=\\
s.t.= \left\{
\begin{array}{lr}
\nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
\lambda \ge 0
\end{array}
\right.
\end{align}
\]





