13 | 因果推断 ¶
约 4489 个字 22 张图片 预计阅读时间 18 分钟
进度 10%,待施工中
Acknowledgement¶
本节内容大部分参考《因果推断入门》学习笔记 | Peyton の杂货铺,同时也参考了 B 站教程
推荐入门教材
校内课程:研究生课《因果推断与机器学习》
http://bayes.cs.ucla.edu/PRIMER/
[ 因果推断 ] 增益模型(Uplift Model)介绍(三)_uplift 模型 -CSDN 博客
大白话谈因果系列文章(一
相关与因果 —— 什么是因果推断 ¶
相关性不等于因果性。
最早看到因果推断是在 CC98 论坛上有一次关于军训成绩与大一成绩之间的因果讨论军训成绩真的不重要吗?——用数据来说话 - CC98 论坛,帖主错把相关性当作因果性进行分析,掀起了关于军训与绩点态度的大讨论(十大镜像贴——为什么我认为“军训成绩重要论”是【有害的】 - CC98 论坛
这里节选用户板凳板凳长的一段发言
还是那句话,相关不是因果。即便得出来军训成绩与大一绩点相关的结论,也不能说明“军训成绩对后续的学习成绩到底有没有影响”。 关于相关性和因果性,一个经典的案例是夏季冰淇淋销量与溺水死亡的人数之间的正相关关系:夏季冰淇淋销量越多,溺水死亡的人数越多。但是并非冰淇淋销量上升导致了溺水死亡人数变多,而是夏季的高气温同时影响了冰淇淋销量和溺水死亡人数。 这种共变关系并非因果关系。再以一个浅显的例子说明,路旁小树与小孩身高之间存在正相关关系,但是却并非小树的高度影响了小孩身高,也并非小孩身高影响了小树高度,而是随着时间流逝小孩和树苗都在长高。 忽略了共同影响自变量和因变量的因素可能导致自选择偏误。比如,在军训绩点和大一绩点的关系中,可能一个人积极的学习态度和自律性同时影响了军训绩点和大一绩点,或者适应能力和团队精神同时影响了军训绩点和大一绩点,甚至是颜值同时影响了军训绩点和大一绩点。 这些结论都很平庸了,而且原楼主本来也就是这个意思,即在“真正的结论”的部分“上述若干点特质”的论述——但是这一部分论述,仅仅是经验推断,缺乏因果机制识别,所以这些结论站不住脚。
- 相关性≠因果性:图中是美国 1999-2009 年的自杀人数与科研经费花费的变化图。可以看到两个指标是高度相关。但是他们之间不存在因果性,即不可能因为减少科研经费而导致自杀人数急剧降低。实际上,相关性通常是对称的,因果性通常是不对称的(单向箭头
) ,相关性不一定说明了因果性,但因果性一般都会在统计层面导致相关性。
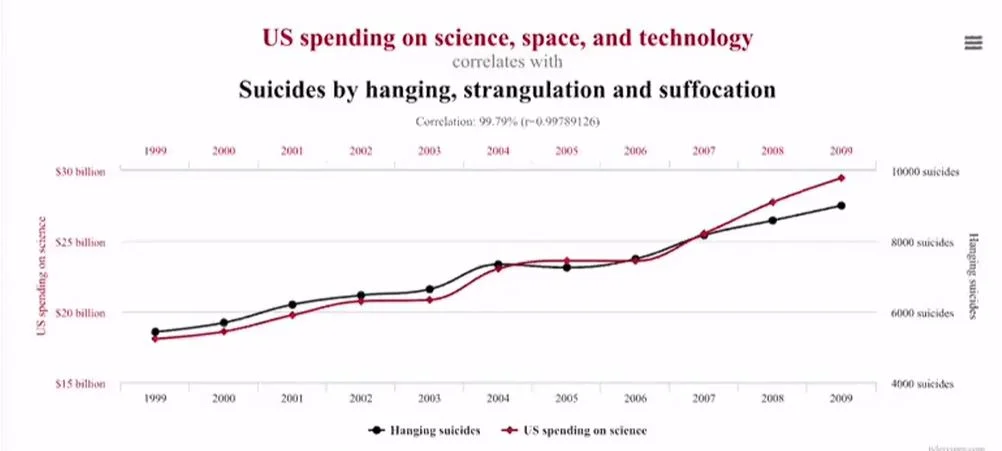
correlation is not equal to causation
因果推断是一整套统计框架
机器学习由模式识别转向因果推断 / 逻辑推断
施加干预可以验证因果性
因果关系有强调前后顺序的区别,而相关关系是依存关系
- 在时间序列上,原因必须出现在结果之前
- 两个变量在经验上有相关性:方向和强度的考量
- 两个变量的因果性不能被第三个变量解释,排除干扰变量
对因果关系的论证需要建立在理论分析的基础上,通过理论分析推断出解释变量和被解释变量之间存在逻辑上的因果关系,最终利用回归分析从实证角度进行理论推理
辛普森悖论:总体数据得到结论和分层得到的结论不一致
不一致的原因:存在干扰的变量——混淆变量
不仅取决于是否吃药(药的作用效果
如果同时影响原因和结果,应该去看分组数据
发展历史 ¶
- 三位因果推断领域著名的科学家:Juden Pearl(UCLA 计算机科学家
) ,Donald Rubin(Harvard 统计学家) ,James Robins(Harvard 流行病学、生物学家) 。
概统基础 ¶
条件独立和独立并不等价
不换门能最后选车,那么一开始就应该选车,概率 \(\frac13\) 换门后选车,一开始应该选门,概率\(\frac13\)
这里举到的例子是开门的例子
证明应该用贝叶斯的
可以这么理解:如果你第不改变选择,说明第一次就选中了 100w,那么 ⅓ 的概率 如果你改变了选择然后选中了 100w,说明你第一次选中的是 1 块,占 ⅔ 的概率
举另一个例子,可能更好更快理解 有 1w 扇门,有 9999 扇都是 1 块钱,只有一扇 100w 你选择一扇门之后,工作人员打开另外 9999 扇门中的 9998 扇,发现都是一块钱,这个时候你换不换
辛普森悖论(Simpson’s Paradox)¶
- 概念:在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论。下面用一个例子来进一步说明这个问题:下面第一个表为男性在接受某种药物治疗后的康复情况,发现经过治疗后的康复率为 0.93,而没有经过药物治疗的康复率为 0.86。第二张表是女性的情况,在经过药物治疗后的康复率为 0.73,而未经过药物治疗的康复率为 0.69。由上面数据我们可以发现:无论是男性女性,药物对治疗该疾病都是有帮助的。
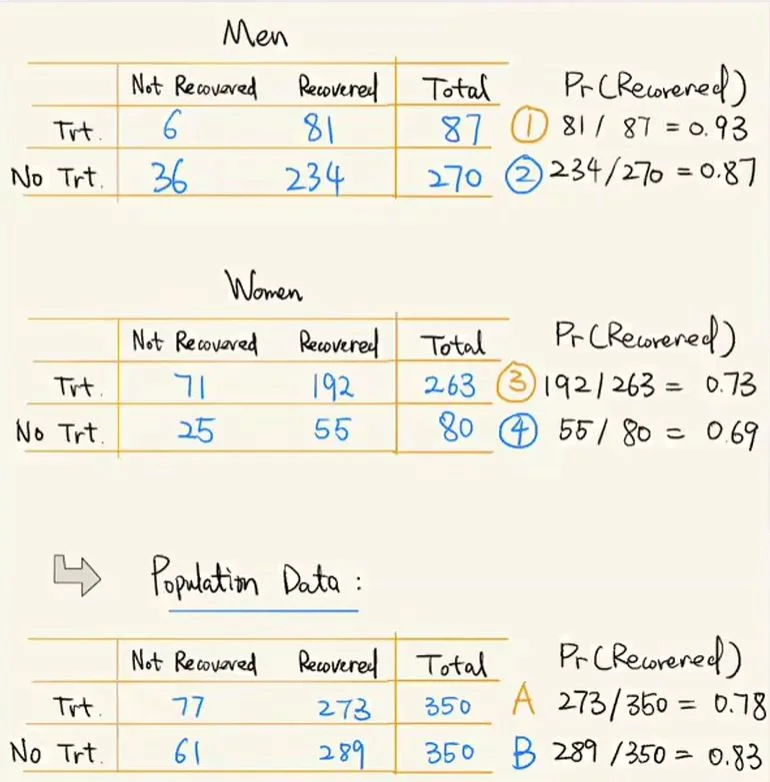
辛普森悖论例子
但是,第三个表格将男女数据全部合并,我们发现:药物对治疗该疾病是没有帮助的,反而是有害的。以上这个问题就是典型的辛普森悖论问题。
-
概率论解释与混淆变量:下面就用概率论的方法来解释上述现象发生的实质和原因。
首先,对变量进行编码表示:
| X | Y | Z | |
|---|---|---|---|
| 0 | Women | Not Recovered | No Treatment |
| 1 | Men | Recovered | Treatment |
那么上述的“辛普森悖论例子”图片中的①、②、③、④、A 以及 B 便可以用条件概率的形式来表示:
①:\(P(Y=1|X=1,Z=1)=0.93\) ②:\(P(Y=1|X=1,Z=0)=0.87\) ③:\(P(Y=1|X=0,Z=1)=0.73\) ④:\(P(Y=1|X=0,Z=0)=0.69\)
\(A\):\(P(Y=1|Z=1)=P(Y=1|Z=1,X=1)·P(X=1|Z=1)+P(Y=1|Z=1,X=0)·P(X=0|Z=1)\) \(B\):\(P(Y=1|Z=0)=P(Y=1|Z=0,X=1)·P(X=1|Z=0)+P(Y=1|Z=0,X=0)·P(X=0|Z=0)\)
这里我们假设 \(P(X=1|Z=1)\) 为 \(q\),则 \(P(X=0|Z=1)\) 为 \(1-q\)。假设 \(P(X=1|Z=0)\) 为 \(p\),则 \(P(X=0|Z=0)\) 为 \(1-p\)。那么 \(A\) 和 \(B\) 便可以表示为:
\(A=①·q+③·(1-q)\) \(B=②·p+④·(1-p)\)
为了更加形象的说明问题,我们将上述的两个式子转化成如下图:
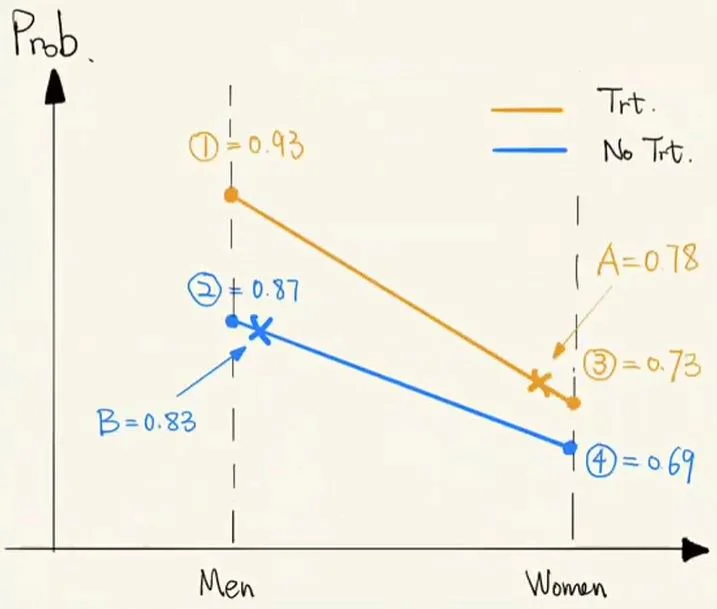
辛普森悖论概率论解释
可见 A 和 B 的取值分别由 p 和 q 取值来决定的。从上图中可以看到,出现 A<B 的内在条件是:1.A 点趋于③的位置(q 趋向于 0,即数据中的药物更多是在女性人群中使用
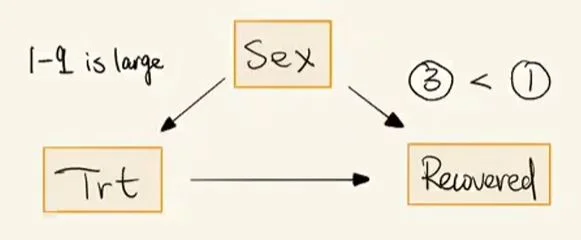
辛普森悖论因素影响图
也就是:性别会影响用药情况和人的恢复,而用药也会影响恢复。这里我们称 Sex 为混淆因素,它不仅会影响我们判断是否用药,也会影响最终的恢复情况。如果你是医生,想要判断该药是否对病情有恢复作用,就必须把 Sex 这一混淆因素去除掉。而去除混淆变量的方法很简单,我们只需要看分组数据(只看男性数据或者只看女性数据,而不是将男女数据合到一起而引入了混淆因素
-
因果中间变量:相对于上述的混淆变量,这里还有一类变量:因果中间变量。下面同样以一个例子来说明。
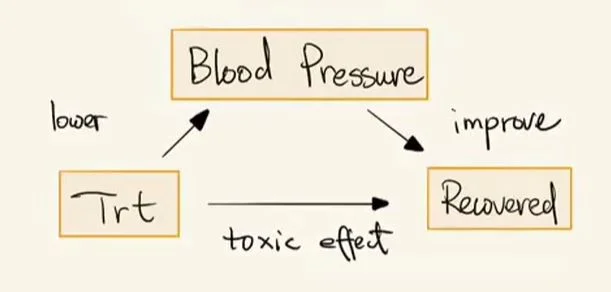
因果中间变量
上图中有三个因素:血压,是否用药以及治疗效果。其中用药对治疗效果有副作用,而另一方面用药可以降血压进一步来提升治疗效果。这里的血压我们称之为“因果中间变量”。

因果中间变量实例
上图是一组实际中的例子。第一行为低血压人群用药的治疗结果:对于没用药有 93% 治愈率,而对于用药人群只有 87% 的治愈率。第二行为高血压人群,对于没用药有 73% 治愈率,而对于用药人群只有 69% 的治愈率。通过这两行分类数据发现:无论是高血压人群还是低血压人群,药物只体现了其对康复的副作用。而第三行,将高血压和低血压人群合并,发现得到了药物对治疗有促进作用。如果你是医生,想知道药物对治疗疾病的真正效果,你会从分类角度(高血压 \ 低血压独立来看)还是整体角度来看?如果从分类的角度,则只是单独考虑了药物的副作用而忽略了血压的影响,但事实上药物对治疗的影响还存在一部分是血压带来的效益。所以从分类角度来看是有问题的。所以,对于这种因果中间变量模型,我们应该从整体的角度来评估药物对治疗的效果。
主要方法和流派 ¶
Causal Discovery,即因果关系的挖掘 ¶
研究因果关系应该研究因果通路
D-sep 算法:判断有向图中任意两个节点的相关性
概统前置知识 ¶
- 条件概率(Conditional Probability
) :
- 独立事件(Independence
) :
Independence: $\(P(A|B) = P(A)\)$
Conditional Independence: $\(P(A|B,C) = P(A|C)\)$
其中 Independence 和 Conditional Independence 是不相等的,如上式中,给定 C 使得 A 和 B 是条件独立的,但我们是无法得到 A 和 B 是独立的。举个例子:A 打电话与 B 打电话本身是独立事件,但是我们假定 A 和 B 都给你打电话,如果你的电话响了,那么对于你来说电话要么是 A 打的要么是 B 打的,这样 A 和 B 事件就是相关了。
- 贝叶斯法则(Bayes' rule
) :
- 期望(Expectation
) :
样本估计: $\(\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i\)$
条件期望: $\(E(Y|X=x) = \sum_y yP(Y=y|X=x)\)$
- 方差(Variance
) :
样本估计: $\(\hat{\sigma}_x^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})^2\)$
- 协方差(Covariance
) :
样本估计: $\(\hat{\sigma}_{XY} = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})\)$
- 相关系数(Correlation
) :
样本估计: $\(\hat{\rho}_{XY} = \frac{\hat{\sigma}_{XY}}{\hat{\sigma}_X \hat{\sigma}_Y}\)$
外生节点 - 集合 U - 根节点
内生节点 - 集合 V - 有父节点的集合
v-structure
- 有相关性,未必有因果性
- 有因果性,大部分时候有相关性,但也不一定
- 特殊例子:
- 原癌基因和抑癌基因
- 正是因为特殊例子,因果推断才困难
图基础知识 ¶
- 完全图(Complete graph):图中任意两个节点之间都存在一条连边。
- Parent 和 Child 节点:如果有一条有向边,那么这条有向边的起始点为 Parent 节点,而终止点为 Child 节点。
- ancestor 和 descendent:如果两个节点被一条有向路径连接,那么第一个节点被在这条路径上称为其他节点的 ancestor,而其他节点是第一个节点的 descendent。具体可以见下图所示。
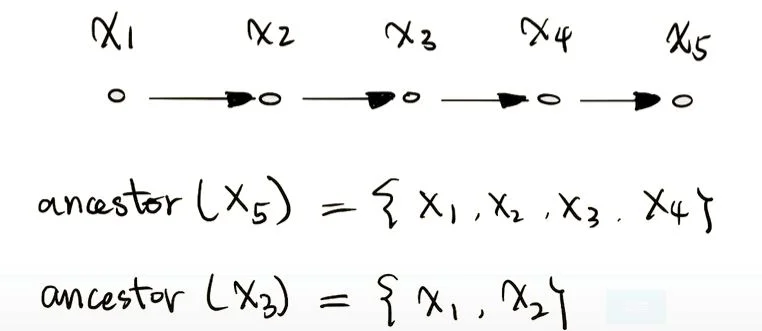
祖先与后代
- 闭环图(cyclic
) :含有闭环的有向图,如下图所示:
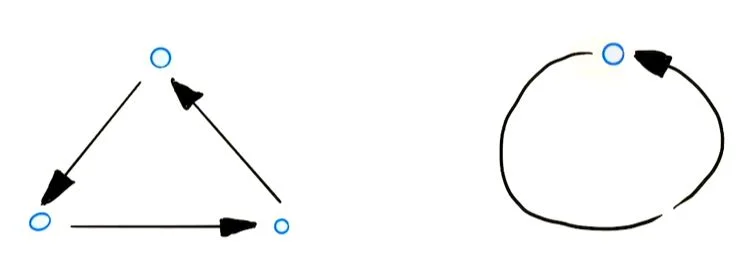
Cyclic
- 非闭环图(acyclic directed graph)DAG:不含闭环的有向图,如下图所示:
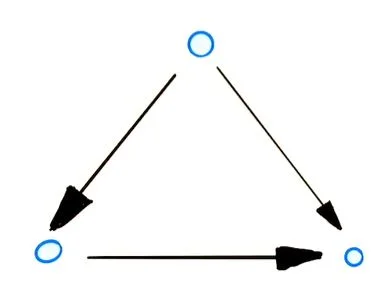
Cyclic
结构因果模型(Structural Causal Model)¶
SCM 这个结构中有一个重要假设叫 sufficiency assumption 即我们没有 unobserved confounder,confounder 就是同时对 t 和 y 都有因果影响的变量,这里要求所有的 confounder 都在我们的数据特征 X 中。所以前期的很多方法都需要满足这个假设
- 结构因果模型(SCM)刻画:假设原因 X 导致了结果 Y,那么这种直接关系就可以用 Y=f(X) 这一结构因果模型来表示。另一种情况,如果原因 X 导致结果 Z,而结果 Z 导致结果 Y,那么这种间接关系可以用 Y=f(g(X)) 这一结构因果模型来表示。无论是直接还是间接,X 都是 Y 的原因(cause
) 。
- 因果、SCM 以及图模型关系:下面就用 3 个例子来说明现实世界中的因果如何转化成结构因果模型以及图模型。首先,是直接因果关系的情况,即只需一条有向边表示即可。
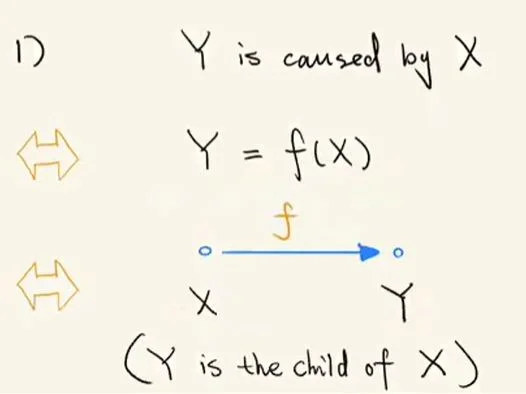
结构因果模型 1
其次是结果 Y 由两个原因 X、Z 共同导致的情况:
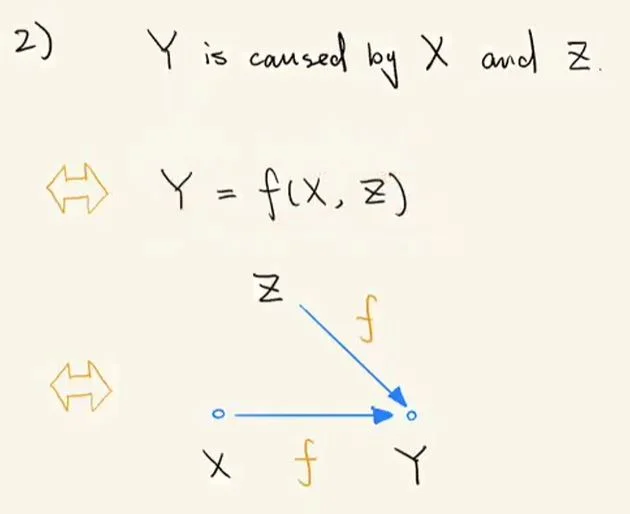
结构因果模型 2
最后是间接因果关系的情况,即前面提到复合函数的情况。
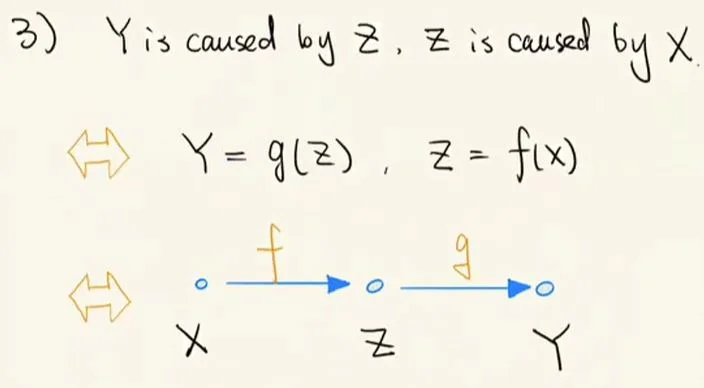
结构因果模型 3
- 外生节点与内生节点:上面我们提到了 3 种比较简单的因果模型,下面我们来看一个相对复杂一点的因果图模型。如下图,原因 X 和 W 共同导致了结果 Z,而结果 Z 导致了结果 Y。那么我们便可以画出对应的因果图模型如下所示。在图中,我们称 X 和 W 这类没有父亲的节点为外生节点(exogenous
) ,而称 Z 和 Y 这类有父亲的节点为内生节点(endogenous)。即:根节点<=>外生节点集合 U,根节点的后代节点(descendent)<=>内生节点集合 V,连边<=>对应的函数映射。
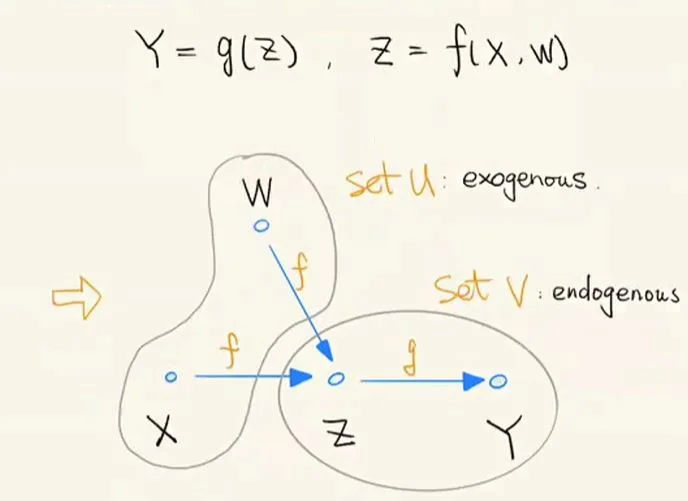
外生节点与内生节点
6. 因果与相关(Intransitive Case)
- 1. 如果两个变量统计相关,那么这两个变量未必具有因果性。
- 2. 如果两个变量存在因果性,那么这两个变量在大多数情况下是统计相关的,但未必一定相关。
- 下面用一个例子来说明上述结论 2 中“未必相关”的部分,下面是该例子的结构因果模型:
SCM:V={X,Y,Z},U={UX,UY,UZ},F={fx,fy,fz}fx:X=Uxfy:Y={aifX=1,Uy=1bifX=2,Uy=1cifUy=2fz:Z={iifY=c,Uz=1jifUz=2
根据上述的结构因果模型可以作得对应的图模型:
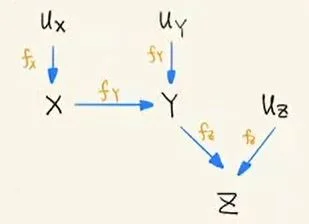
Intransitive case 图模型
从模型中我们可以发现,P(Z=i)=P(Z=i|X=1)=P(Z=i|X=2) 三者都是相等,即 Z 的取值实际上和 X 没有关系,而完全取决于 Uy 和 Uz,Z 和 X 之间便是独立的。因此,实际上两个还有因果关系的变量也未必存在统计相关性,这也给因果推断带来了困难。
链式结构(Chain)¶
- V-Structure 的三种结构:①chain、②fork、③collider(所谓 V-structure 就是含有三个顶点的图,是图模型的基本组件,掌握了这三个基本组件便一通百通
) ,具体对应的图模型见下图所示。
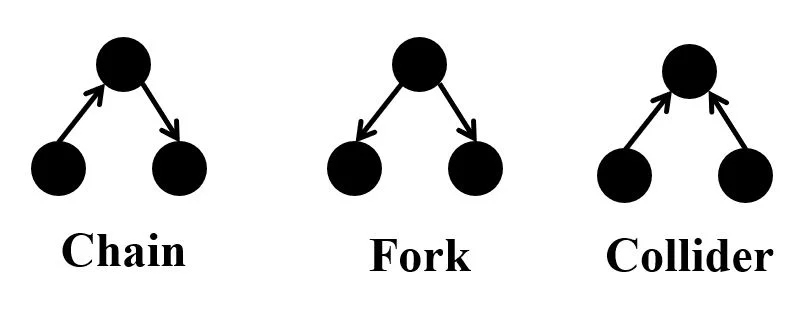
V-Structure
- Chain 上的条件独立结论:从下图(题注为:Chain 的性质)中,我们发现
X和Z之间存在很多的链式结构。按照前几节的内容可以得到下面结论:X与Y1...Yn都是大概率统计相关的,且Z与Y1...Yn也是大概率统计相关的。进一步可以得到Z和X也是大概率统计相关。
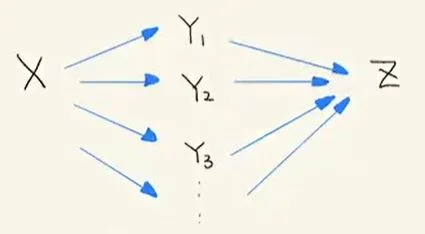
Chain 的性质
但是如果其中的Y是已知条件(即 Condition 在Y1..Yn上所有通路X和Z便是统计独立的(相当于X和Z间所有通路断开)——这是链式结构的重要性质。
8. 叉式结构(Fork)¶
- Fork 上的条件独立结论:从下图(题注为:Fork 的性质)中,我们发现
Ux、Uy以及Uz为三个外生变量,而X、Y和Z之间构成了 Fork 结构。按照前几节的内容可以得到下面结论:X与Y都是大概率统计相关的,且X与Z也是大概率统计相关的。进一步可以得到Y和Z也是大概率统计相关。
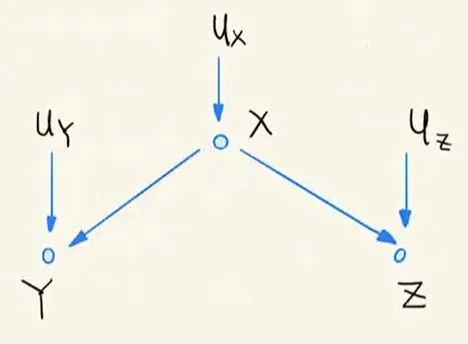
Fork 的性质
但是如果其中的X是已知条件(即 Condition 在X上Y和Z便是统计独立的(相当于Y和Z间不存在通路)——这是叉式结构的重要性质。
9. 对撞结构(Collider)¶
Collider 上的条件独立结论:从下图(题注为:Collider 的性质)中,我们发现Ux、Uy以及Uz为三个外生变量,而X、Y和Z之间构成了 Collider 结构。按照前几节的内容介绍,可以得到下面结论:X与Z都是大概率统计相关的,且Y与Z也是大概率统计相关的。而X和Y却是大概率统计独立的。
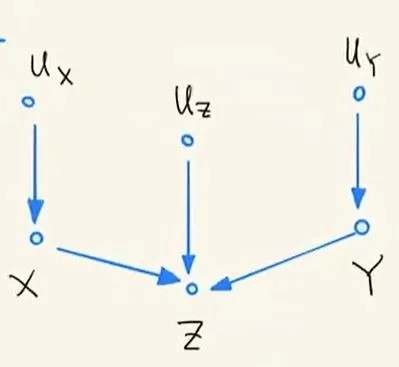
Collider 的性质
但是如果其中的Z是已知条件(即 Condition 在Z上X和Y便是统计相关的——这是对撞结构的重要性质。
注:如果Z还存在后代,那么 Condition 在Z后代上,X和Y依旧是大概率统计相关的。
D- 分隔(D-Separation) | 判断图中任意两个节点的相关性 ¶
- D- 分隔定义:有向图相关性的分隔。通过第 7、8、9 章的介绍,我们可以得到下表的结论:
| V-Structure | Uncondition | Condition |
|---|---|---|
| Fork | Unblock | Block |
| Chain | Unblock | Block |
| Collider(or descendents) | Block | Unblock |
注:其中的 Unblock 为 dependent,而 Block 为 independent。
- 对于Fork:X<—Z—>Y,
X和Y是 d-connected 的,即前面提到的 Unblock(连通通路) 。 - 对于Chain:X—>Z—>Y,
X和Y是 d-connected 的,即前面提到的 Unblock(连通通路) 。 - 对于Collider:X—>Z<—Y,
X和Y是 d-separated 的,即前面提到的 Block(阻断通路) 。
- 如果
X和Y是 d-connected,那么X和Y是相关的。反之,如果X和Y是 d-separated,那么X和Y是独立的。
- 在 Uncondition 的时候,对撞结构会阻断通路。而叉状和链状结构会连通相关通路。如果 Condition 在叉状和链状结构上,通路会被阻断;而 Condition 在对撞结构或其子节点上,通路就被打开。
- 如果
X和Y之间的每一条通路都被阻断,那么X和Y就被 D- 分隔。另一方面,如果X和Y之间存在一条通路连通,那么X和Y就是 D- 连接。
- 对于复杂的图,只要拆分成 V-structure 就可以用 D-Separation 理论来分析。下面是一个复杂图的 D- 分隔分析方法。其中
, ’≡‘表示变量间相关,而‘⊥’表示变量间独立。
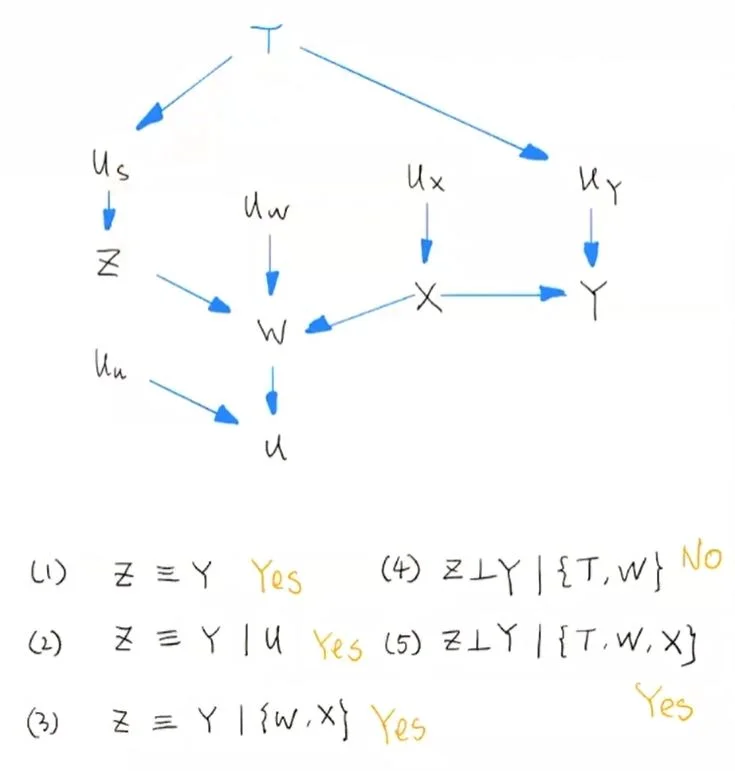
复杂图的 D-Separation
模型检验和等价类(Model Testing and Causal Search)¶
- 模型检验:通过给定图模型,可以从中确定出各个变量间的因果关系和统计相关性。而在实际中我们往往有这些变量的统计数据,需要做的就是从统计数据中估计出变量间的相关性和因果性,这里估计的方法有很多,如:变量间的线性回归或者非线性回归等等。图模型得到的因果推断和数据统计得到的因果结论应该是统一的,这便有了模型检验。
-
等价类:从前面的介绍我们可以得到 Fork 和 Chain 的很多性质都是相同的。但 Chain 和 Collider,Fork 和 Collider 的性质差异都很大。即:
- 叉状和链状结构在统计相关性上是等价的。
- 对撞和链式结构并不等价。
- 对撞和叉状结构也不等价。
- 有连通父节点的对撞结构也是等价类的一种情况
。 (collider 的两个父节点之间存在连边)
判断两个有向图等价就看他们是否有相同的骨架,也就是在两个有向图里去掉等价类的部分之后,剩下的部分是否等价。
乘积分解法则(Rule of Product Decomposition)¶
含义:对于每一个结构化因果模型所对应的联合分布,都可以进行乘积分解,这种乘积分解可以大大的减少联合分布的参数空间维度,使得在数据量有限的情况下,对因果模型联合分布有效的估计成为了可能。这种乘积分解将联合分布分解成若干项,每一项都是模型中的一个变量基于其父节点的条件概率。乘积分解公式的推导基于条件概率公式,用到了 D-Separation 中的链状结构。最终得到乘积分解法则:
P(X1,X2,…Xn)=Πni=1P(Xi|pa(Xi))
其中 pa(Xi) 是变量 Xi 的所有父节点。
下面用一个例子来证明该法则:
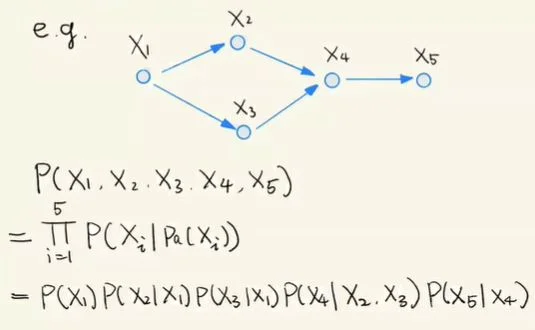
乘积分解法则例子
实际上只要证明下面的等式,而下面的等式只需要根据 D-Separation 即可得到。
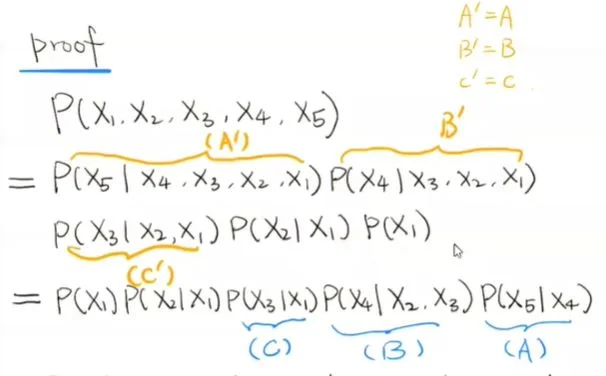
乘积分解法则证明
如何构建因果图 ¶
度量方法 ¶
ATE,CATE,ITE,
- 假设一个人没有去医院,他的健康状况是 \(Y_{0i}\),假设他去医院接受了治疗,他的健康状况是 \(Y_{1i}\)
- 我们想要的因果效应: $\(TE_{i} = Y_{1i} - Y_{0i}\)$
- 显然,我们并不可能同时观测到 \(Y_{0i}\) 和 \(Y_{1i}\)
- 假设 \(D_{i}\) 是人是否去医院的选择,那我们观察到的观测结果为 \(Y_{i}\) $$ Y_{i} = begin{cases} Y_{1i}, & text{if } D_{i} = 1 \ Y_{0i}, & text{if } D_{i} = 0 end{cases}$$
- 潜在结果模型:可观测结果和不可观测结果的关系式。 $\(Y_{i} = Y_{0i} + D_{i}(Y_{1i} - Y_{0i})\)$
对于我们想研究的一项政策 / 项目 / 干预,我们想得到其平均处理效应(Average Treatment Effect)
ATE 的计算公式里我们可以看出其中隐含的一条重要假设:个体处理效应独立(stable unit treatment value assumption, SUTVA
那么什么时候我们需要估计 ITE 呢?当整个 population 是 heterogeneous 的时候,即人群有异质性的时候,ATE 可能会误导结论。举个例子,我们衡量大众点评评分对餐馆的销量影响的时候,ATE 可能会误导,因为大城市的餐馆可能会更多被大众点评影响,小城市或农村可能影响更小。这时候其实我们要评估的每一个 subpopulation 的 ATE,也即 CATE(或者细粒度到每个 individual 的 ITE
假设:线性性质 + 同质性
ITE: Individual Treatment Effect
ATE : Average Treatment Effect
ATT : Average Treatment Effects on Treated
CATE: Conditional Average Treatment Effect
大白话
ITE:个体的因果效应,也可以看成是个体的 CATE
ATE:平均处理效应,如 AB 实验,受处理和未受处理的人群的效果的差的期望
ATT:受处理的人群的平均处理效应,受处理的人群通过 PSM 方法找出和他们一样的人做为替身,看他们的效果的差别
CATE:人群中某个 subgroup 的平均处理效应
ITE(Individual Treatment Effect)表示一个 individual 的 treatment effect。那么如果我们想看一个大群体(一个普遍现象
注意到,我们想要的是某个个体给券不给券的区别,而不是总体给券不给券的区别,所以这里就不是研究 ATE(average treatment effect
例子
如 Burde and Linden (2013) 论文中的例子
的例子,要比较村里有小学和村里没有小学(通勤去距离较远的小学)的孩子,他们的成绩表现是否有差别。
这里 ATE 是 text{ATE} = E[Y_{ij1}−Y_{ij0}] ,代表村里有小学和村里没有小学的成绩表现差异的期望。那有人会说,这些孩子可能本来就有特征差异,比如村里有小学,可能他们家庭条件就比较好。那这里 ATT 登场了,就来控制他们的这些混淆变量。
这里 ATT 是 ATT=E[Y_{ij1}−Y_{ij0}|T_{k} = 1] ,假设村里有小学的孩子,他们如果村里没有小学,会是什么样的表现呢?同一个人肯定没有办法既受处理又不受处理。那只能在没有小学的群体中用 PSM 等方法,找出和他们各种特征非常相似的人,如家庭背景、年龄啊,作为他们的替身。这样子就能在理想化的情况下,求同一批小孩,他们在有小学和没有小学的表现是否有差异。
CATE 呢?举一个增长领域的例子,我们考虑到投入和产出,要把钱花在刀刃上。人群中有些人是无论你推广了还是不推广,它都不会转化。我们应该要把钱投入到那些”如果不推广他们就不会转化,但是推广了就会转化的“人群身上,这就是 subgroup,我们就要计算给他们投放广告,能带来多少的效果提升(uplift
那什么情况下 CATE 是会等于 ATE 呢?当没有 effect modification(修饰效应)的时候,CATE=ATE。
修饰效应是什么呢?修饰效应指的是有没有一个因素的的不同,使得 treatment 对 outcome 的作用也产生了差异。比如是否存在某些因素使得 subgroup 和整个人群 population 的效果产生差异呢,是存在的,就是我们刚刚提到的人群特征。并且正是有了 effect modification 的存在,我们需要按照 effect modification 进行划分。
再举一个例子,实验看抽烟是否会导致肺癌。这里有一个性别的变量,如果性别的变量仅仅造成男女抽烟的比例不同,那它是一个 confounder(混淆变量
随机试验 ¶
- 观测数据
- 随机实验数据:可以证明因果性
随机试验是一种去除 cofounder 的方法:A/B test,外界的其他 confound 因素都去掉了
- 实验的数据是有干预的,数据生成机制发生了改变
混淆变量(Confounding Variable)¶
- 代表原因的变量:Treatment,代表结果的变量:Outcome。
- 混淆变量(Confounding Variable/Confounder
) :同时影响原因和结果的变量。混淆变量会引入非因果的统计相关性。
-
观测数据(Observational Study) VS 实验数据(Experiment)
- 观测数据是由被动观测和收集产生。观测数据中数据采集源和采集环境没有受到影响和干预。
- 实验数据是干预的环境下得到的结果。一般是先干预再观测。
例如:要想研究锻炼和感冒的关系。随机取选择样本,记录每一个人的锻炼量和感冒次数就属于观测数据。而实验数据:随机选择参与者,其中一部分进行干预(锻炼
) ,而另一部分不进行干预(不锻炼) ,记录感冒的次数。
- 随机试验一般是先招募试验个体,然后随机的给受验个体指定 Treatment 和 Control,然后再比较 Outcome 的区别。
- 观测数据中变量可能呈现相关性,但只有试验数据可以直接验证因果关系。因为随机实验能够去掉 Confounding 的影响。
观测数据与试验数据(Observation Study And Experiment)¶
- 观测数据中可能体现的仅仅是统计相关性,而可靠的试验数据可能直接揭示因果性,因为观测数据往往受混淆变量的影响,而随机试验可以消除这种影响。
- 随机试验使得试验组和对照组中个体的混淆变量的分布相同,因此 Outcome 的变化就可以归咎于 Treatment 的影响。
消除混淆:后门准则(Backdoor Criterion)¶
有了 d- 分离的概念基础,我们就可以回到一开始提到的混淆的问题,按照之前所述,我们希望消除混淆因子带来的“伪相关”,找出真正的因果关系。一种消除混杂的方法叫后门准则(backdoor criterion
变量 A 和 Y 之间的后门路径就是连接 A 和 Y 但是箭头不从变量 A 出发的路径。比如:A←L→Y,便称为 A 和 Y 之间的后门路径(backdoor path
后门准则可以简述如下:如果我们有足够的数据能够将所有A和Y 之间的后门路径全部阻断,那么我们就可以识别(identify)A和 Y之间的因果关系。
简单来说,混淆(confounding)就是因果变量之间的共因。而混淆因子(confounder)就是能够阻断因果变量之间所有后门路径的变量(可能混杂因子不止一个
因此,混淆因子也可以被更准确地定义如下:
- 【从结构角度定义】如果以某个变量 L 为条件使得变量 A 和 Y 之间的相关性发生了更改(即原来相关变为不相关、原来不相关变为相关
) ,那么该变量 L 为 A 和 Y 之间的混杂因子。 - 【从传统角度定义】当变量 L 满足以下三个条件时,L 便是 A 和 Y 之间的混淆因子:
- L 与 A 相关
- 当以 A 为条件时 L 与 Y 相关
- L 不在 A 到 Y 的因果关系路径中
要注意的是,结构角度的定义并不一定得到正确的判断,很多情况下会带来选择偏倚等错误判断,所以两个角度结合起来判断更好。
G-estimation¶
通过假想的随机试验进行计算
举一个西普森悖论的例子,相当于在 condition 上进行观测
没有混淆变量,干预与否不影响结果
- 干预前后 Y 的生成机制没有变化
准试验 ¶
Matching 匹配:常见的策略是 PSM(Propensity Score Matching,PSM 详解 ->
*Matching 缺点就是会浪费一些数据,同事对于高维的情况,我们会难以判断两个样本是否相似。
图:matching 概念图解
Weighting 加权:常用的策略是 IPW(Inverse Probability Weighting Estimator,IPW 详解 ->
理论上可以证明 IPW 估计出来的差异是 ATE(Average Treatment Effect,即我们想要知道的 treatment 的效果)的无偏估计,但是当具有某种特性的 x 的 units 在实验组或者对照组出现的比例很小的时候,会导致我们估计出来的倾向性得分趋进于 0 或者 1,然而倾向性得分是在 units 的权重函数的分母上面的,使得 IPW 虽然无偏(bias=0)但是波动很大(variance 很大
*IPW 的准确性直接取决于倾向性分数的构建
工具变量 Instrumental Variable, IV ¶
工具变量(IV)是一种用于解决回归分析中内生性问题的方法。内生性问题通常由于遗漏变量、测量误差、反向因果等原因导致解释变量与误差项相关,从而使得普通最小二乘法(OLS)估计结果有偏或不一致。
工具变量的核心思想 ¶
工具变量的核心思想是找到一个与解释变量相关,但与误差项不相关的变量,通过这个变量来估计解释变量对因变量的因果效应。工具变量应满足以下条件:
- 相关性:工具变量与解释变量存在相关性
- 外生性:工具变量与误差项不相关,即它不应该受到模型中其他变量的影响
- 排他性:工具变量不应该直接影响因变量,除了通过解释变量之外
个体分类 ¶
在工具变量分析中,根据个体对处理变量(解释变量)和工具变量的反应,可以将个体分为以下几类:
- Always Taker(始终接受者
) :无论工具变量取何值,这些个体总是会接受处理 - Never Taker(从不接受者
) :无论工具变量取何值,这些个体都不会接受处理 - Defier(反抗者
) :这些个体的行为与工具变量和处理变量的预期关系相悖 - Complier(依从者
) :这些个体的行为与工具变量的预期关系一致
判断个体类型 ¶
要判断个体属于哪一类,需要了解个体在工具变量(A)和处理变量(L)上的取值情况:
| 类型 | 条件 |
|---|---|
| Always Taker | 无论 A 的取值如何,L 总是为 1 |
| Never Taker | 无论 A 的取值如何,L 总是为 0 |
| Defier | A=1 时 L=0,或 A=0 时 L=1 |
| Complier | A=1 时 L=1,A=0 时 L=0 |
CAET 与识别方法 ¶
CAET(Causal Average Effect of Treatment,平均处理效应)是工具变量分析中的一个重要概念,它指的是在工具变量的作用下,处理变量对因变量的平均因果效应。
在工具变量分析中,通常关注的是依从者的平均处理效应(Complier Average Treatment Effect,CATE
反事实 ¶
很多时候我们无法做随机试验,无法干预数据,因果推断的主要话题也是围绕观测数据而展开的
condition 是观察数据,do 是随机 实验
- association
- intervention
- counterfactuals: parallel universe
对同一个个体构建一个相反的结果,观测结果的差异
同时去过医院和没有去过医院的差异(没有去过医院是去过医院的反事实,是无法观测到的)
常见的方法有:增益模型(Uplift model
Uplift model:用于估算 ITE(Individual Treatment Effect