05 | 平稳过程 ¶

约 4156 个字 6 张图片预计阅读时间 16 分钟

Cheet Sheet¶

本章题目比较格式化，大概都是这种流程，背公式就行了，对常用的傅立叶变换对要记忆清楚

一般都是第一问算均值和自相关函数，然后验证是不是宽平稳过程（有独立的就拆开，没有的利用 pdf 进行积分）
第二问算时间均值和时间相关函数，然后验证均值和自相关的各态历经性
求谱密度（与傅立叶变换相联系）

① 证明是宽平稳过程

$E[X(t)]$ 为常数
$R_X$ 为只和 $\tau$ 有关的函数

② 均值各态历经

$\langle X(t)\rangle\equiv\mu_X$
$\lim_{T\rightarrow\infty} \frac1T\int_0^\infty C_x(\tau) d\tau$
在 $\underset{\tau\rightarrow+\infty}\lim R_X(\tau)$ 存在的条件下，证明 $\underset{\tau\rightarrow+\infty}\lim R_X(\tau)=\mu_X^2$

③ 自相关函数各态历经

$\langle X(t)X(t+\tau)\rangle\equiv R_X(\tau)$

④ 功率谱密度：对自相关函数进行傅里叶变换 ; 实、非负、偶函数

\[ \begin{cases} P_{\xi}(\omega) = \int_{-\infty}^{+\infty} R(\tau) e^{-j\omega\tau} \, \mathrm{d}\tau \\ R(\tau) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} P_{\xi}(\omega) e^{j\omega\tau} \, \mathrm{d}\omega \end{cases} \]

傅立叶变换的性质：时域相乘等于频域卷积

时域	频域
$e^{-a\mid\tau\mid}$	$\frac{2a}{a^2+\omega^2}$
$\frac{sin\omega_0\tau}{\pi\tau}$	$\begin{cases}1\quad\mid\omega\mid\leq\omega_0\\[2ex]0\quad\mid\omega\mid>\omega_0\end{cases}$
$1$	$2\pi\delta(\omega)$
$\delta(\tau)$	$1$
$cos\omega_0\tau$	$\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]$

\[ \begin{aligned} e^{j\omega_0 \tau} &= \cos(\omega_0 \tau) + j\sin(\omega_0 \tau) \\ e^{-j\omega_0 \tau} &= \cos(\omega_0 \tau) - j\sin(\omega_0 \tau) \end{aligned} \]

因此

\[ \begin{aligned} \cos(\omega_0 \tau) &= \frac{1}{2}(e^{j\omega_0 \tau} + e^{-j\omega_0 \tau}) \\ \sin(\omega_0 \tau) &= \frac{1}{2j}(e^{j\omega_0 \tau} - e^{-j\omega_0 \tau}) \end{aligned} \]

平稳随机过程 ¶

一维分布与时间 $t$ 无关

二维分布只与时间间隔 $\tau$ 有关

均值和 $t$ 无关
方差与 $t$ 无关
自相关函数与时间间隔有关，与时间起点无关

无线电设备中热噪声电压 $X(t)$ 是由于电路中电子的热运动引起的，这种热扰动不随时间而变；连续测量飞机飞行速度产生的测量误差$X(t)$，是由很多因素（如仪器振动、电磁波干扰、气候等）引起的，但主要因素不随时间而变；

严平稳过程 ¶

各维概率密度函数都不随时间的推移而变化

$\{X(t);t\in T\}$ 中所有 $X_t$ 同分布，且 $\forall\;n\geq2\quad(X_{t_1},X_{t_2},\dots,X_{t_n})$ 的分布仅与时间差 $t_i-t_{i-1}$ 有关，而与起始时间 $t_1$ 无关。

宽平稳过程 ¶

均值为常数，自相关函数仅仅是时间间隔的函数

存在二阶矩的严平稳过程。平稳过程均指宽平稳过程。

均值函数：$\mu_X(t)=E[X(t)]=E[X(0)]\overset{记为}\Longrightarrow\mu_X\;$( 常数 )
方差函数：$D[X(t)]=R_X(0)-\mu_X^2\;$( 常数 )
自相关函数：
- $E[X(t)X(t+\tau)]=E[X(0)X(\tau)]=R_X(\tau)$( 为时间差的函数 )
- $E[X^2(t)]=R_X(0) = Var(X)$( 常数 )
自协方差函数：$C_X(\tau)=R_X(\tau)-\mu_X^2$

平稳相关过程 ¶

若 { $X(t);t\in T$ }、{ $Y(t);t\in T$ } 是两个平稳过程，$X(t),Y(t)$ 的互相关函数也为时间差 $\tau$ 的函数 $\overset{记为}\Longrightarrow R_{XY}(\tau)$，称 $X(t),Y(t)$ 是平稳相关 / 联合（宽）平稳的。

平稳过程自相关函数的性质 ¶

功率特性
- $R_X(0)=E[X^2(t)]=\psi_X^2\geq0 = S$
  - 物理意义 : 随机过程的平均功率
- $R(\infty) = E^2[\xi(t)] = a^2$
  - 物理意义 : 随机过程的直流功率
  - 推导 : 时间间隔无限大时 , $\xi(t)$ 与 $\xi(t+\tau)$ 趋于独立
  - $R(\infty) = \lim_{\tau \to \infty} E[\xi(t)\xi(t+\tau)] = \lim_{\tau \to \infty} E[\xi(t)]E[\xi(t+\tau)] = E[\xi(t)]E[\xi(t)] = E^2[\xi(t)]$
- $R(0) - R(\infty) = E[\xi^2(t)] - a^2 = \sigma^2$
  - 物理意义 : 随机过程的交流功率对应方差公式
对称性
- $R_X(-\tau)=R_X(\tau)$ ( 偶函数 )
- $R_{XY}(-\tau)=R_{YX}(\tau)$ ( 非奇非偶 )
有界性
- $\mid R_X(\tau)\mid\leq R_X(0)$
- $\mid C_X(\tau)\mid\leq C_X(0)=\sigma_X^2$
  - 给出了自相关函数的上界 , 与自身时刻相关性最大
- $\mid R_{XY}(\tau)\mid^2\leq R_X(0)R_Y(0)$
- $\mid C_{XY}(\tau)\mid^2\leq C_X(0)C_Y(0)$
- 相关 / 协方差函数在时间差 $\tau$ 为 0 时取得最大值
非负定性 $R_X(\tau)$ 是非负定的，即 $\forall\;t_1,t_2,\dots,t_n\in T$ 和 $\forall\;a_1,a_2,\dots,a_n\in R$ ，有

$$ sum_{i,j=1}^n R_X(t_i-t_j)a_ia_jgeq0 $$
周期性 $\{X(t);t\in T\}$ 是周期为 $T_0$ 的平稳过程 $\Leftrightarrow$ $R_X(t)$ 是周期为 $T_0$ 的函数

各态历经性 ¶

只有一个样本函数，如何刻画

$x(t)$ 为随机过程的任意一个实现（样本函数）

时间均值 ¶

$\langle X(t)\rangle=\underset{T\rightarrow+\infty}\lim\frac 1{2T}\int_{-T}^TX(t)dt$

$\langle X_n\rangle=\underset{N\rightarrow+\infty}\lim \frac 1N\sum_{n=1}^NX_n$

时间相关函数 ¶

$\langle X(t)X(t+\tau)\rangle=\underset{T\rightarrow+\infty}\lim\frac 1{2T}\int_{-T}^TX(t)X(t+\tau)dt$

$\langle X_nX_{n+m}\rangle=\underset{N\rightarrow+\infty}\lim \frac 1N\sum_{n=1}^NX_nX_{n+m}$

各态历经性 ¶

均值具有各态历经性 $P(\langle X(t)\rangle=\mu_X)=1$ / $P(\langle X_n\rangle=\mu_X)=1$ （即时间均值恒等于均值函数）

自相关函数具有各态历经性 $\forall\;\tau\quad P(\langle X(t)X(t+\tau)\rangle=R_X(\tau))=1$ （即时间相关函数恒等于自相关函数）

含义：

随机过程中的任一实现都经历了随机过程的所有可能状态
化“统计平均”为“时间平均”，用任意一个样本函数刻画整个随机过程的所有特征，简化实际的测量和计算

各态历经性推出平稳 ; 平稳不能推导各态历经性

均值各态历经定理 ¶

设 $\{X(t), -\infty < t < \infty\}$ 为平稳过程，则 $P\left\{ \langle X(t) \rangle = \mu_X \right\} = 1$, 等价于 $\lim_{T \to +\infty} \frac{1}{T} \int_0^T C_X(\tau) \, d\tau = 0$

推论：在 $\underset{\tau\rightarrow+\infty}\lim R_X(\tau)$ 存在的条件下，若 $\underset{\tau\rightarrow+\infty}\lim R_X(\tau)=\mu_X^2$ ，则均值具有各态历经性，反之不具有。

平稳过程的功率谱密度 ¶

定义 ¶

假定 $f(t)$ 为随机过程 $\xi(t)$ 的任一实现，对其进行 $T$ 长度的截断，记为 $f_T(t)$，其傅里叶变换为 $F_T(\omega)$，则任一实现的功率谱为：

\[ P_f(\omega) = \lim_{T \to \infty} \frac{|F_T(\omega)|^2}{T} \]

故 $\xi(t)$ 的功率谱密度为：

\[ P_{\xi}(\omega) = E\left[P_f(\omega)\right] = \lim_{T \to \infty} \frac{E\left[|F_T(\omega)|^2\right]}{T} \]

维纳 - 辛钦定理 ¶

$S_X(\omega)$ 是 $\omega$ 的非负实偶函数，与自相关函数 $R_X(\tau)$ 是一对 $Fourier$ 变换对。

平稳随机过程 $\xi(t)$ 的功率谱密度函数 $P_{\xi}(\omega)$ 和自相关函数 $R(\tau)$ 为一对傅里叶变换对。

\[ \begin{cases} P_{\xi}(\omega) = \int_{-\infty}^{+\infty} R(\tau) e^{-j\omega\tau} \, \mathrm{d}\tau \\ R(\tau) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} P_{\xi}(\omega) e^{j\omega\tau} \, \mathrm{d}\omega \end{cases} \]

或

\[ \begin{cases} P_{\xi}(f) = \int_{-\infty}^{+\infty} R(\tau) e^{-j2\pi f\tau} \, \mathrm{d}\tau \\ R(\tau) = \int_{-\infty}^{+\infty} P_{\xi}(f) e^{j2\pi f\tau} \, \mathrm{d}f \end{cases} \]

\[ R(\tau) \Leftrightarrow P_{\xi}(f) \]

$\omega = 2\pi\cdot f$ 所以积分的时候有变换关系

因为 $S_X\;R_X$ 都是实偶函数，所以 $R_X\overset{F}\longleftrightarrow S_X\quad S_X\overset{F}\longleftrightarrow 2\pi R_X$

性质 ¶

实、非负、偶

功率谱密度具有非负性：$P_{\xi}(f) \geq 0$

功率谱密度是偶函数：$P_{\xi}(-f) = P_{\xi}(f)$

单边、双边功率谱密度互换：$P_{\xi\text{单边}}(f) = \begin{cases} 2P_{\xi\text{双边}}(f) & f \geq 0 \\ 0 & f < 0 \end{cases}$

平均功率计算方法 ¶

利用自相关函数计算

\[ S = R(0) = E\left[\xi^{2}(t)\right] \]

利用功率谱密度

\[ S = \int_{-\infty}^{+\infty} P_{\xi}(f) \, \mathrm{d}f = \frac{1}{2\pi} \int_{-\infty}^{+\infty} P_{\xi}(\omega) \, \mathrm{d}\omega \]

常用傅立叶变换对 ¶

这部分的题目和信号与系统相关知识联系比较紧密，可以对照着进行学习

时域	频域
$e^{-a\mid\tau\mid}$	$\frac{2a}{a^2+\omega^2}$
$\begin{cases}1-\frac{\mid\tau\mid}{T}\quad\mid\tau\mid\leq T\\[2ex]0\quad\mid\tau\mid>T\end{cases}$	$(\frac{sin(\omega T/2)}{\omega T/2})^2$
$\frac{sin\omega_0\tau}{\pi\tau}$	$\begin{cases}1\quad\mid\omega\mid\leq\omega_0\\[2ex]0\quad\mid\omega\mid>\omega_0\end{cases}$
$1$	$2\pi\delta(\omega)$
$\delta(\tau)$	$1$
$cos\omega_0\tau$	$\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]$
$R_X(\tau)cos\omega_0\tau$	$\frac12[S_X(\omega+\omega_0)+S_X(\omega-\omega_0)]$

各种常见信号傅里叶变换需要记住

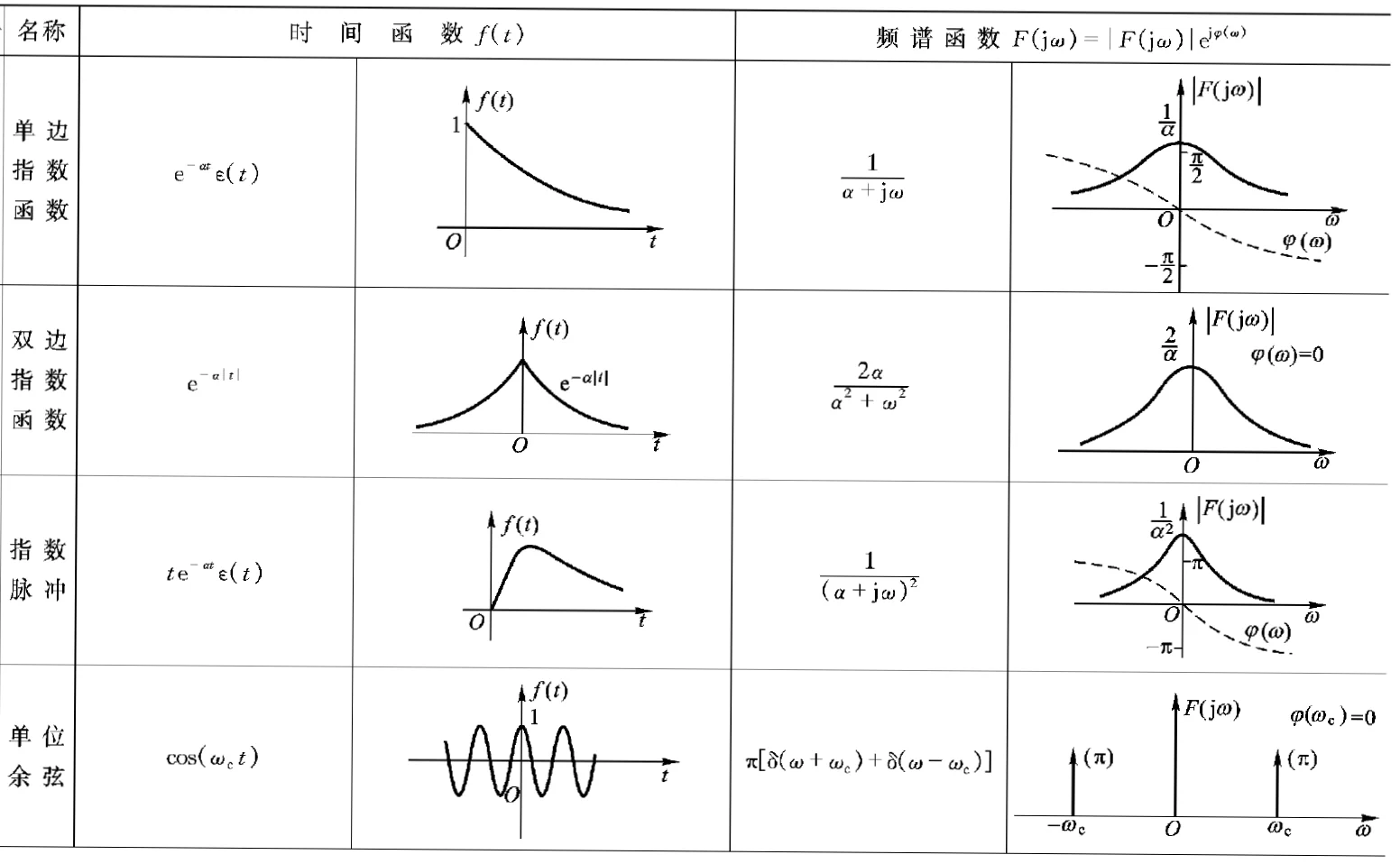
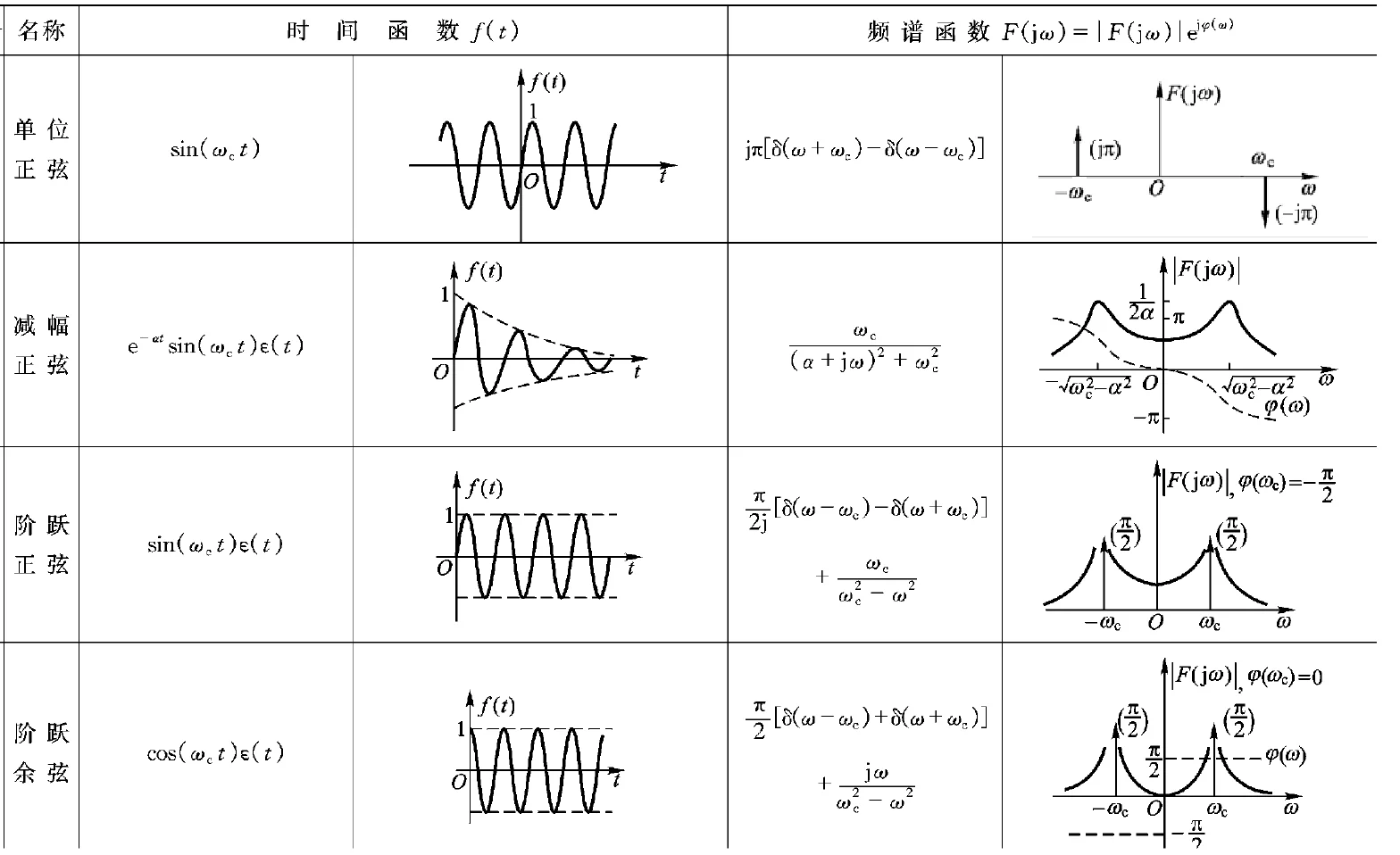
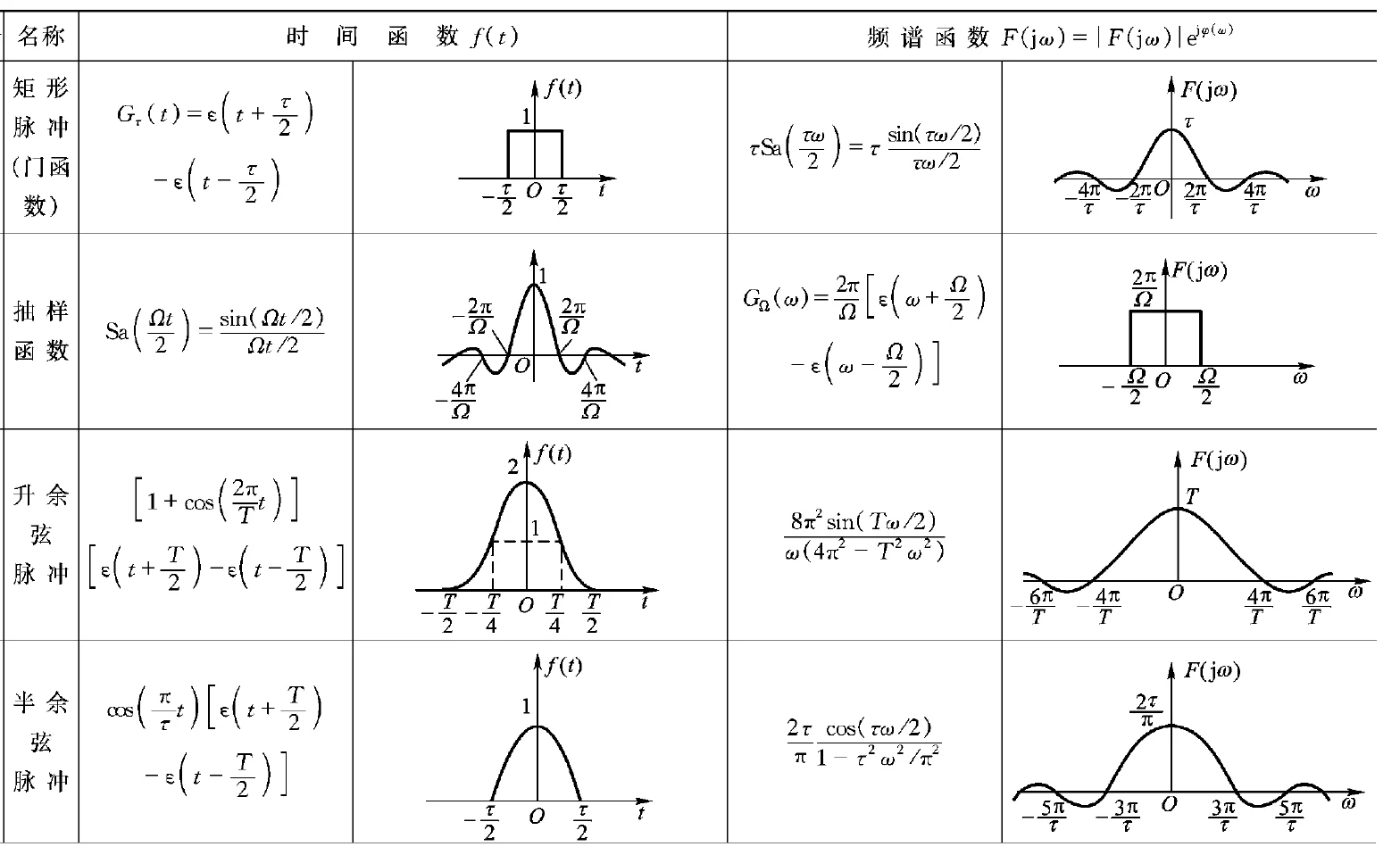
$cos(\omega_0 t)$ 频谱搬移
门函数的表达 $u(t) - u(t-t_0)$

互谱密度 ¶

设 $X(t)$ 和 $Y(t)$ 是两个平稳相关的随机过程 ,

定义 : $S_{XY}(\omega) = \lim_{T \to +\infty} \frac{1}{2T} E \left\{ F_X(-\omega, T) F_Y(\omega, T) \right\}$ 为平稳过程 $X(t)$ 和 $Y(t)$ 的互谱密度。

它有以下特性 :

$S_{XY}(\omega) = S_{YX}^*(\omega)$, 即 $S_{XY}(\omega)$ 和 $S_{YX}(\omega)$ 互为共轭函数
当 $\int_{-\infty}^{+\infty} |R_{XY}(\tau)| d\tau < \infty$ 时 , 成立维纳 - 辛钦公式 $S_{XY}(\omega) = \int_{-\infty}^{+\infty} R_{XY}(\tau) e^{-i\omega\tau} d\tau, \quad R_{XY}(\tau) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} S_{XY}(\omega) e^{i\omega\tau} d\omega;$

例题 ¶

严平稳 ¶

例 5.1.1

设 $\{X_{n}; n=1,2,\cdots\}$ 是随机变量序列 , $E(X_{n})=\mu$, $D(X_{n})=\sigma^{2}$.

(1) 若 $X_{1},X_{2},\cdots$ 两两不相关 , 问 $\{X_{n};n=1,2,\cdots\}$ 是否为宽平稳序列 ?

(2) 若 $X_{1},X_{2},\cdots$ 独立同分布 , 问 $\{X_{n};n=1,2,\cdots\}$ 是否为严平稳序列 ?

(3) 若 $X_{1},X_{2},\cdots$ 两两不相关 , 对 $n\geqslant 1$,

\[ X_{2n-1}\sim N(\mu,\sigma^{2}),\quad X_{2n}\sim U(\mu-\sqrt{3}\sigma,\mu+\sqrt{3}\sigma) \]

这里 $\sigma^{2}>0$. 问 $\{X_{n};n=1,2,\cdots\}$, 是否为宽平稳序列 ? 是否为严平稳序列 ?

(1) 当 $\{X_{n};n=1,2,\cdots\}$ 是两两不相关随机变量序列时 , 由条件知 , $E(X_{n})=\mu$,

\[ R_{X}(n,m)= \begin{cases} \sigma^{2}+\mu^{2}, & n=m, \\ \mu^{2}, & n\neq m, \end{cases} \quad n,m=1,2,\cdots, \]

即均值函数是常数 , 自相关函数只与 $n-m$ 有关 , 因此 $\{X_{n};n=1,2,\cdots\}$ 是宽平稳序列 .

(2) 当 $\{X_{n};n=1,2,\cdots\}$ 是相互独立随机变量序列时 , 设 $X_{n}$ 的分布函数为 $F(x)$, 对 $n_{1}<n_{2}<\cdots<n_{k}$, $(X_{n_{1}},X_{n_{2}},\cdots,X_{n_{k}})$ 在点 $(x_{1},x_{2},\cdots,x_{k})$ 处的分布函数值

\[ F(x_{1},x_{2},\cdots,x_{k};n_{1},n_{2},\cdots,n_{k})=F(x_{1})F(x_{2})\cdots F(x_{k}) \]

而 $(X_{n_{1}+m},X_{n_{2}+m},\cdots,X_{n_{k}+m})$ 在点 $(x_{1},x_{2},\cdots,x_{k})$ 处的分布函数值

\[ F(x_{1},x_{2},\cdots,x_{k};n_{1}+m,n_{2}+m,\cdots,n_{k}+m)=F(x_{1})F(x_{2})\cdots F(x_{k}) \]

由定义知 , $\{X_{n};n=1,2,\cdots\}$ 是严平稳序列 .

例 5.1.2

设 $X$ 是一个非常值随机变量 , 对任何 $n \geq 1$, 令 $Y_n = X$. 问 $\{Y_n;n = 1,2,\cdots\}$ 是否为严平稳序列 ? 当 $E(X^2) < \infty$ 时 , $\{Y_n;n = 1,2,\cdots\}$ 是否为宽平稳序列 ?

对任何 $k \geq 1$, $n_1, n_2,\cdots, n_k \geq 1$, $m \geq 1$, 有

\[ (Y_{n_1},Y_{n_2},\cdots,Y_{n_k})=(\underbrace{X,X,\cdots,X}_{k个})\\ =(Y_{n_1+m},Y_{n_2+m},\cdots,Y_{n_k+m}) \]

所以 $\{Y_n;n = 1,2,\cdots\}$ 为严平稳序列 .

当 $E(X^2) < \infty$ 时 , $E(Y_n) = E(X)$ 存在且为常数 , $E(Y_mY_n) = E(X^2)$ 为常数 . 所以 $\{Y_n;n = 1,2,\cdots\}$ 为宽平稳序列 .

求解宽平稳、各态历经性、谱密度 ¶

例题

已知信号过程 $[X(t);\, t \geq 0]$，满足 $P(X(t) = \pm 1) = \frac{1}{2}$，且在区间 $(t, t+\tau]$ 内取正负号的次数服从参数为 $\lambda \tau$ 的泊松分布。另有过程 $Y(t) = \cos(t - \theta)$，$-\infty < t < +\infty$，其中 $\theta$ 在区间 $(0, 2\pi)$ 上服从均匀分布。$\{X(t);\, t \geq 0\}$ 与 $\{Y(t);\, -\infty < t < +\infty\}$ 相互独立。定义 $Z(t) = X(t)Y(t) + 1$，$0 \leq t < +\infty$。请回答下列问题：

$\{X(t);\, t \geq 0\}$ 的均值函数 $\mu_X(t)$ 和自相关函数 $R_X(t, t+\tau)$ 为
- (A) $\mu_X(t) = 0$，$R_X(t, t+\tau) = \dfrac{1}{2} e^{-2\lambda \tau}$
- (B) $\mu_X(t) = 0$，$R_X(t, t+\tau) = e^{-2\lambda \tau}$
- (C) $\mu_X(t) = 0$，$R_X(t, t+\tau) = \dfrac{1}{2} e^{-2\lambda |\tau|}$
- (D) $\mu_X(t) = 0$，$R_X(t, t+\tau) = e^{-2\lambda |\tau|}$
$\{X(t);\, t \geq 0\}$ 的谱密度函数 $S_X(\omega)$ 为
- (A) $\dfrac{2\lambda}{\lambda^2 + \omega^2}$
- (B) $\dfrac{4\lambda}{2\lambda^2 + \omega^2}$
- (C) $\dfrac{2\lambda}{4\lambda^2 + \omega^2}$
- (D) $\dfrac{4\lambda}{4\lambda^2 + \omega^2}$
$\{Y(t);\, -\infty < t < +\infty\}$ 的时间均值 $\langle Y(t) \rangle$ 为
- (A) $0$
- (B) $\cos t$
- (C) $\sin(t - \theta)$
- (D) $\cos(t - \theta)$
$\{Y(t);\, -\infty < t < +\infty\}$ 的时间相关函数 $\langle Y(t) Y(t+\tau) \rangle$ 为
- (A) $0$
- (B) $\cos 2\tau$
- (C) $\cos \tau$
- (D) $\dfrac{1}{2} \cos \tau$
$\{Y(t);\, -\infty < t < +\infty\}$ 的各态历经性为
- (A) 均值、自相关函数都不具有各态历经性
- (B) 均值具有各态历经性，但自相关函数不具有各态历经性
- (C) 自相关函数具有各态历经性，但均值不具有各态历经性
- (D) 均值、自相关函数都具有各态历经性
下列等式中正确的是
- (A) $\mu_Z(t) = \mu_X(t)\mu_Y(t)$
- (B) $R_Z(t, t+\tau) = R_X(t, t+\tau) + R_Y(t, t+\tau)$
- (D) $R_Z(t, t+\tau) = R_X(t, t+\tau) R_Y(t, t+\tau) + 1$
- (C) $\mu_Z(t) = \mu_X(t) + \mu_Y(t) + 1$
关于 $\{Z(t);\, t \geq 0\}$ 的叙述错误的是
- (A) $\{Z(t);\, t \geq 0\}$ 是平稳过程
- (B) $\{Z(t);\, t \geq 0\}$ 的自相关函数为 $\dfrac{1}{2} e^{-2\lambda|\tau|} \cos\tau + 1$
- (C) $\{Z(t);\, t \geq 0\}$ 的谱密度函数为 $\dfrac{\lambda}{4\lambda^2 + (\omega-1)^2} + \dfrac{\lambda}{4\lambda^2 + (\omega+1)^2} + \pi\delta(\omega)$
- (D) $\{Z(t);\, t \geq 0\}$ 的均值具有各态历经性 $

答案： DDADDDC

其中 $X(t)$ 题干比较难以理解，但其实作为选择题可以交叉排除做出来。

顺序是：

$X(t)$ 均值、自相关、谱密度、时间均值、时间自相关
$Y(t)$ 均值、自相关、谱密度、时间均值、时间自相关

求 $Z(t)$ 的谱密度的时候，可以使用时域相乘等于频域卷积的性质，但是要注意公式前面的 $\frac{1}{2\pi}$ 不要遗漏

均值函数 $\mu_X(t)$ 由于 $X(t)$ 在任一时刻取值为 $\pm 1$ 且概率各为 $1/2$，其期望为：

\[ \mu_X(t) = \mathbb{E}[X(t)] = \frac{1}{2}(1) + \frac{1}{2}(-1) = 0. \]

因此所有选项中均值函数均为 0，符合题设。

自相关函数 $R_X(t, t+\tau)$ 需计算 $\mathbb{E}[X(t)X(t+\tau)]$。由题意可知：

$X(t)$ 在区间 $(t, t+\tau)$ 内的符号翻转次数 $N(\tau)$ 服从参数为 $\lambda\tau$ 的泊松分布。
$X(t+\tau)$ 的符号取决于 $N(\tau)$ 的奇偶性：若 $N(\tau)$ 为偶数（含 0 次），则 $X(t+\tau) = X(t)$；若为奇数，则 $X(t+\tau) = -X(t)$。

因此：

\[ X(t+\tau) = X(t) \cdot (-1)^{N(\tau)}, \]

代入自相关函数得：

\[ \begin{align*} R_X(\tau) &= \mathbb{E}[X(t)X(t+\tau)] = P(N(\tau) \text{取偶数})\cdot 1 + P(N(\tau) \text{取奇数}) \cdot (-1)\\ &= \sum_{k=0}^{\infty} \frac{(\lambda\tau)^k}{k!} e^{-\lambda\tau} (\text{偶数}) - \sum_{k=0}^{\infty} \frac{(\lambda\tau)^k}{k!} e^{-\lambda\tau}(\text{奇数}) \\ &= \sum_{k=0}^{\infty} \frac{(-\lambda\tau)^k}{k!} e^{-\lambda\tau} \quad \text{把-1乘进去}\\ &= e^{-\lambda\tau} \cdot e^{-\lambda\tau} \quad \text{级数的性质}\\ &= e^{-2\lambda|\tau|} \end{align*} \]

本题目改编自课本例 5.1.6

设 $\{X(t);-\infty<t<\infty \}$ 是宽平稳过程，$X(t)=Acos(t+2\pi B)$ ，$A,B$ 独立且服从 $(0,1)$ 上的均匀分布

\[ E[A]=\frac12\quad D[A]=\frac1{12}\quad E[A^2]=E^2[A]+D[A]=\frac 13 \]

（1）均值函数

\[ \mu_X=E[Acos(2\pi B)]=0 \]

（2）自相关函数

\[ \begin{align*} R_X(\tau)&=E[X(0)X(\tau)]\\ &=E[A^2]\cdot E[cos(2\pi B)\cdot cos(\tau+2\pi B)]\\ &=\frac{cos\tau}{6} \end{align*} \]

（3）谱密度

\[ S_X(\omega)=\frac\pi6[(\omega+1)+(\omega-1)] \]

（4）时间均值

\[ \begin{align*} \langle X(t)\rangle&=\underset{T\rightarrow+\infty}\lim\frac 1{2T}\int_{-T}^TX(t)dt\\ &=\underset{T\rightarrow+\infty}\lim\frac 1{T}\int_0^{T}Acos(t+2\pi B)\\ &=A\underset{T\rightarrow+\infty}\lim \frac{ \sin(T+2\pi B) - \sin(2\pi B)}{T}\\ &=0\equiv\mu_X \end{align*} \]

具有各态历经性。

（5）时间相关函数

\[ \langle X(t)X(t+\tau)\rangle=\underset{T\rightarrow+\infty}\lim\frac 1{2T}\int_{-T}^TX(t)X(t+\tau)dt\\ =\frac{A^2cos\tau}2\neq R_X(\tau)\]

不具有各态历经性。

（6）综合（4）（5），$X(t)$ 不是各态历经过程。

已知随机过程 $\xi(t)=A\cos(\omega_{c}t+\theta)$，$A$ 和 $\omega_{c}$ 均为常数。$\theta$ 在 $[0,2\pi]$ 均匀分布。$f(\theta)=\frac{1}{2\pi}$，$\theta\in[0,2\pi]$。

1) 证明 $\xi(t)$ 广义平稳；期望为常数，$R(t,t+\tau)=R(\tau)$。

\[ \begin{aligned} E[\xi(t)] &= \int_{0}^{2\pi}A\cos(\omega_{c}t+\theta)\cdot\frac{1}{2\pi}d\theta \\ &= \frac{A}{2\pi}\int_{0}^{2\pi}(\cos\omega_{c}t\cdot\cos\theta-\sin\omega_{c}t\cdot\sin\theta)d\theta \\ &= \frac{A}{2\pi}[\cos\omega_{c}t\int_{0}^{2\pi}\cos\theta d\theta-\sin\omega_{c}t\int_{0}^{2\pi}\sin\theta d\theta] \\ &= 0 \text{ (为常数)} \end{aligned} \]

\[ \begin{aligned} R(t,t+\tau) &= E[\xi(t)\xi(t+\tau)] \\ &= E[A\cos(\omega_{c}t+\theta)\cdot A\cos(\omega_{c}(t+\tau)+\theta)] \\ &= \frac{1}{2}[\cos(\alpha-\beta)+\cos(\alpha+\beta)] \\ &= \frac{A^{2}}{2}E[\cos(2\omega_{c}t+\omega_{c}\tau+2\theta)+\cos(\omega_{c}\tau)] \\ &= \frac{A^{2}}{2}\cos\omega_{c}\tau+\int_{0}^{2\pi}\cos(2\omega_{c}t+\omega_{c}\tau+2\theta)\cdot\frac{1}{2\pi}d\theta \\ &= \frac{A^{2}}{2}\cos\omega_{c}\tau \end{aligned} \]

只与 $\tau$ 有关。

$\therefore \xi(t)$ 广义平稳

2) 求 $\xi(t)$ 的功率谱密度和平均功率

\[ \begin{aligned} R(t) &= \frac{A^2}{2} \cos(w_c t) \iff P_{xx}(w) = \frac{\pi A^2}{2} [\delta(w + w_c) + \delta(w - w_c)] \\ \cos(w_c t) &\iff \pi [\delta(w + w_c) + \delta(w - w_c)] \\ \end{aligned} \]

方法 1 求 $R(0)$:

\[ S = R(0) = \frac{A^2}{2} \]

方法 2 求积分 :

\[ \begin{aligned} S &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} P_{xx}(w) dw \\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} \frac{\pi A^2}{2} [\delta(w + w_c) + \delta(w - w_c)] dw \\ &= \frac{1}{2\pi} \cdot 2 \cdot \frac{\pi A^2}{2} = \frac{A^2}{2} \\ \end{aligned} \]

注意到

\[ \int_{-\infty}^{+\infty} \delta(t) dt = 1 \]

3) 判断 $\xi(t)$ 是否具有各态历经性

\[ \xi ( t ) = A \cos ( w c t + \theta ) \]

\[ \begin{aligned} \overline { a } &= \lim _ { T \rightarrow \infty } \frac { 1 } { T } \int _ { - \frac { T } { 2 } } ^ { \frac { T } { 2 } } A \cos ( w c t + \theta ) d t = 0 \\ \overline { a } &= a \end{aligned} \]

\[ \begin{aligned} \overline { R ( \tau ) } &= \lim _ { T \rightarrow \infty } \frac { 1 } { T } \int _ { - \frac { T } { 2 } } ^ { \frac { T } { 2 } } A \cos ( w c t + \theta ) \cdot A \cos [ w c ( t + \tau ) + \theta ] d t \\ &= \lim _ { T \rightarrow \infty } \frac { A ^ { 2 } } { 2 T } \cdot T \cdot \cos w c \tau \\ &= \lim _ { T \rightarrow \infty } \frac { A ^ { 2 } } { 2 T } \int _ { - \frac { T } { 2 } } ^ { \frac { T } { 2 } } [ \cos ( 2 w c t + w c \tau + 2 \theta ) + \cos ( w c \tau ) ] d t \\ &= \frac { A ^ { 2 } } { 2 } \cos w c \tau \\ \end{aligned} \]

\[ \begin{aligned} \overline { R ( \tau ) } &= R ( \tau )\\ &= \lim _ { T \rightarrow \infty } \frac { A ^ { 2 } } { 2 T } [ \cos w c \tau \int _ { - \frac { T } { 2 } } ^ { \frac { T } { 2 } } d t + \int _ { - \frac { T } { 2 } } ^ { \frac { T } { 2 } } \cos ( 2 w c t + w c \tau + 2 \theta ) d t ] \end{aligned} \]

例题 3

已知随机过程 $z(t)=m(t)\cos(\omega_{c}t+\theta)$，$m(t)$ 为广义平稳过程，其自相关函数为 $R_{m}(\tau)=\begin{cases}1+\tau & -1<\tau<0 \\1-\tau & 0<\tau<1 \\0 & \text{其他}\end{cases}$

随机变量 $\theta$ 在 $[0,2\pi]$ 服从均匀分布，与 $m(t)$ 统计独立。

1）证明 $z(t)$ 广义平稳

\[ \begin{aligned} E[z(t)] &= E[m(t)\cos(\omega_c t + \theta)] \\ &= E[m(t)] \cdot \frac{\int_0^{2\pi} \cos(\omega_c t + \theta) \frac{1}{2\pi} d\theta}{1} \\ &= 0 \\ R_z(t, t + \tau) &= E[z(t)z(t + \tau)] \\ &= E\left\{m(t)\cos(\omega_c t + \theta) \cdot m(t + \tau)\cos[\omega_c(t + \tau) + \theta]\right\} \\ &= E\left\{m(t) \cdot m(t + \tau) \cdot \frac{1}{2}\cos(2\omega_c t + \omega_c \tau + 2\theta) + \frac{1}{2}\cos\omega_c \tau\right\} \\ &= R_m(\tau) \cdot \frac{1}{2} E\left[\cos(2\omega_c t + \omega_c \tau + 2\theta) + \cos\omega_c \tau\right] \\ &= \frac{1}{2} R_m(\tau) \cdot \cos\omega_c \tau \end{aligned} \]

所以是广义平稳

2）求自相关函数 $R_{z}(\tau)$ 并画出波形

\[ \begin{align*} R_{z}(\tau) &= \frac{1}{2} R_{m}(\tau) \cos \omega_{c} \tau\\ &=\begin{cases} \frac{1}{2} (1+\tau)\cos \omega_{c} \tau & -1 < \tau < 0 \\ \frac{1}{2} (1-\tau)\cos \omega_{c} \tau & 0 < \tau < 1 \\ 0 & \text{其他} \end{cases} \end{align*} \]

所以在画图的时候，先画出包络，再绘制函数

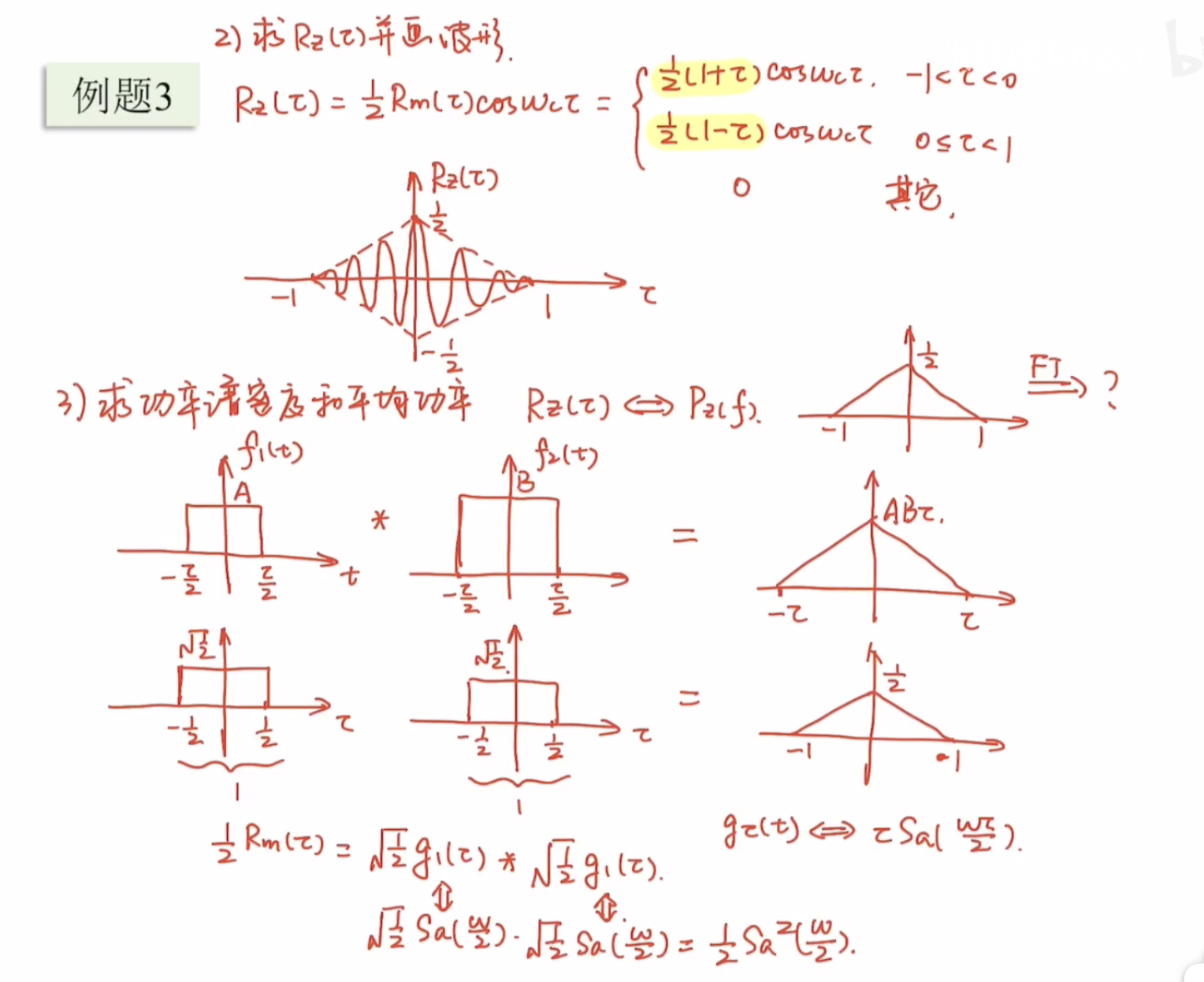
3）求功率谱密度 $P_{z}(f)$ 及功率

\[ R_{z}(\tau) = \frac{1}{2} R_{m}(\tau) \cos \omega_{c} \tau \]

$R_M$ 是一个三角波，我们已知三角波可以由两个门函数卷积而来，所以我们可以将 $R_M$ 分解为两个门函数，然后对每个门函数进行傅里叶变换，最后将两个门函数的傅里叶变换相乘，得到 $P_{z}(\omega)$。

\[ \begin{align*} P_{z}(\omega) &= \mathcal{F}(f_{1}(t) \cdot f_{2}(t)) =\frac{1}{2\pi} F_{1}(\omega) * F_{2}(\omega) \\ &= \frac{1}{2\pi}\cdot {\color{red}\mathcal{F}(\frac{1}{2}R_m(\tau))}\cdot{\color{blue}\mathcal{F}(\cos(\omega_c\tau))}\\ &= \frac{1}{2\pi} \cdot {\color{red}\frac{1}{2} Sa^{2}(\frac{\omega}{2}) }\cdot {\color{blue} \pi [\delta(\omega + \omega_{c}) + \delta(\omega - \omega_{c})]}\\ &= \frac{1}{4} [Sa^{2}(\frac{\omega + \omega_{c}}{2}) + Sa^{2}(\frac{\omega - \omega_{c}}{2})] \end{align*} \]

\[ \because\omega = 2\pi f \]

\[ P_{z}(f) = \frac{1}{4} \{Sa^{2}[\pi(f + f_{c})] + Sa^{2}[\pi(f - f_{c})]\} \]

平均功率

\[ S = R_{z}(0) = \frac{1}{2} \]

例题 5

设 $\{X(t);-\infty < t < \infty\}$ 是宽平稳过程，若自相关函数 $R_X(\tau)=2\delta(\tau)+2$，则谱密度 $S_X(\omega)=$ __，$\{X(t)\}$ 的均值各态历经当且仅当均值 $\mu_X=$ ____。

解：

1. 求谱密度 $S_X(\omega)$

答案：$2+4\pi\delta(\omega)$

2. 求均值 $\mu_X$

答案：$\pm\sqrt{2}$

例题 6

设 $\{X(t);-\infty<t<\infty\}$ 是宽平稳过程，若均值函数 $\mu_{X}=2$，自相关函数 $R_{X}(\tau)=e^{-|\tau|}+a$，则 $\{X(t)\}$ 的谱密度 $S_{X}(\omega)=$_，均值各态历经当且仅当均值 $a=$ ___。

答案：

$\frac{2}{1+\omega^{2}}+2\pi a\delta(\omega)$
$4$

例题 7

设 $\{B(t);t\geq0\}$ 是标准布朗运动，$A\sim N(1,1)$，且 $A$ 与 $\{B(t);t\geq0\}$ 独立。设 $X(t)=A[B(t+1)-B(t)]$，$t\geq0$。

1. 计算 $\{X(t)\}$ 的均值函数和自相关函数，并证明它是宽平稳过程

(1)$\mu_X(t)=EX(t)=0$

\[ \begin{aligned} R_X(t,t+\tau) &= EX(t)X(t+\tau) \\ &= \begin{cases}2(1-|\tau|), & |\tau|\leq1; \\ 0, & |\tau|>1.\end{cases} \end{aligned} \]

因为 $\mu_X(t)$ 是常数 ,$R_X(t,t+\tau)$ 只与 $\tau$ 有关 , 所以 $\{X(t)\}$ 是宽平稳过程。

2. 判断 $\{X(t)\}$ 的均值是否具有各态历经性，并说明理由

(2)$\lim_{\tau\to\infty}R_X(\tau)=0=\mu_X^2$, 所以均值具有各态历经性

例题 8

设 $X(t)=A\cos(t+\Theta)+B$，$-\infty<t<\infty$，这里 $A,B,\Theta$ 相互独立，$A\sim N(1,1)$，$\Theta\sim U(0,2\pi)$，$B$ 具有概率密度 $f(x)=\begin{cases}|x|,&-1<x<1;\\0,&其它.\end{cases}$

1. 计算 $\{X(t)\}$ 的均值函数和自相关函数，并证明它是一个宽平稳过程

(1) $\mu _{X}( t) = 0$

\[R_{X}(t,t+\tau)=\frac{1}{2}+\cos\tau \]

因为 $\mu_{X}(t)$ 是常数，$R_{X}(t,t+\tau)$ 只与 $\tau$ 有关，所以是宽平稳

答案

(1)

$\mu _{X}( t) = 0$
$R_{X}(t,t+\tau)=\frac{1}{2}+\cos\tau$

因为 $\mu_{X}(t)$ 是常数，$R_{X}(t,t+\tau)$ 只与 $\tau$ 有关，所以是宽平稳

(2)

$\langle X( t) \rangle = \operatorname* { lim} _{T\to \infty }\frac 1{2T}\int _{- T}^{T}X( t) dt= B$
$\langle X(t)X(t+\tau) \rangle=\lim_{T\to\infty}\frac{1}{2T}\int_{-T}^{T}X(t)X(t+\tau)dt=\frac{A^{2}}{2}\cos\tau+B^{2}$

(3) 都不具有各态历经性

例题 9

设 $X(t)=A\cos(t+2\pi B)$, $-\infty<t<\infty$, 这里 $A$, $B$ 相互独立同服从区间 $(0,1)$ 上的均匀分布。

1. 计算 $\{X(t); -\infty<t<\infty\}$ 的均值函数和自相关函数 , 并证明它是一个宽平稳过程

(2) 计算 $\{X(t); -\infty<t<\infty\}$ 的时间均值 $\langle X(t) \rangle$ 和时间相关函数 $\langle X(t)X(t+\tau) \rangle$, 判断 $\{X(t); -\infty<t<\infty\}$ 是否为各态历经过程 , 说明理由。

(1) 首先计算均值和自相关函数：

\[ E(A) = 0, \quad E(A^2) = \frac{1}{3} \]

\[ \mu_X(t) = 0 \]

\[ R_X(t, t+\tau) = \frac{\cos\tau}{6} \]

因此，$\{X(t)\}$ 是宽平稳过程。

(2) 计算时间均值和时间相关函数：

时间均值为 $\langle X(t) \rangle = \lim_{T\to\infty} \frac{1}{2T} \int_{-T}^{T} (A\cos(t+2\pi B))\,dt = 0$
由于 $P(\langle X(t) \rangle = \mu_X) = 1$，所以均值具有各态历经性。
时间相关函数为

\[ \begin{aligned} \langle X(t)X(t+\tau) \rangle &= \lim_{T\to\infty} \frac{1}{2T} \int_{-T}^{T} A^2\cos(t+2\pi B)\cos(t+\tau+2\pi B)\,dt \\ &= \frac{A^2\cos\tau}{2} \end{aligned} \]

而 $P(\langle X(t)X(t+\tau) \rangle = R_X(\tau)) = P\left(\frac{A^2\cos\tau}{2} = \frac{\cos\tau}{6}\right) \neq 1$，所以相关函数不具各态历经性，$\{X(t)\}$ 不是各态历经过程。

各态历经定理和推论 ¶

例题

已知谱密度函数 $S_X(\omega) = \frac{\omega^2+5}{\omega^4+10\omega^2+9}$, 则自相关函数 $R_X(\tau) = \underline{\quad\quad}$, 均值 $\mu_X = \underline{\quad\quad}$

解析

记住变换对： $e^{-a\mid\tau\mid}$ 与 $\frac{2a}{a^2+\omega^2}$

先进行因式分解

\[ \begin{aligned} S_X(\omega) &= \frac{\omega^2+5}{\omega^4+10\omega^2+9} \\ &= \frac{\omega^2+5}{(\omega^2+1)(\omega^2+9)} \\ &= \frac{1/2}{\omega^2+1} + \frac{1/2}{\omega^2+9} \end{aligned} \]

再进行傅立叶反变换

\[ \begin{align*} R(\tau) = &\mathcal{F}^{-1} (\frac{1/2}{\omega^2+1} + \frac{1/2}{\omega^2+9}) \\ &= \frac14 e^{-|\tau|}+\frac1{12}e^{-3|\tau|} \end{align*} \]

根据各态历经定理：在 $\underset{\tau\rightarrow+\infty}\lim R_X(\tau)$ 存在的条件下，$\underset{\tau\rightarrow+\infty}\lim R_X(\tau)=\mu_X^2$，所以 $\underset{\tau\rightarrow+\infty}\lim R_X(\tau) = 0$, 所以均值为 0

习题 ¶

各个题目为自己做的答案，欢迎提交 issue 或者 PR 纠错

5.2¶

5.2

设随机过程 $X(t)=A\sin(t+\Theta),-\infty<t<\infty$, 其中随机变量 $A$ 与 $\Theta$ 相互独立，$P\left(\Theta=\frac\pi4\right)=P\left(\Theta=-\frac\pi4\right)=\frac12$，$A$ 服从 $(-1,1)$ 上均匀分布。判断 $\{X(t);-\infty<t<\infty\}$ 是否为平稳过程。

解：

1. 先求均值函数 $\mu_X(t)=E[X(t)]$

\[ \begin{aligned} \mu_X(t) &= E[X(t)] = E[A\sin(t+\Theta)] \\ &= E_A\left[ E_\Theta\left[ A\sin(t+\Theta) \mid A \right] \right] \\ &= E_A[A] \cdot E_\Theta[\sin(t+\Theta)] \quad \text{（$A$与$\Theta$独立）} \end{aligned} \]

由于 $A$ 在 $(-1,1)$ 上均匀分布，$E[A]=0$。

\[ E_\Theta[\sin(t+\Theta)] = \frac12 \sin\left(t+\frac\pi4\right) + \frac12 \sin\left(t-\frac\pi4\right) \]

但 $E_A[A]=0$，所以

\[ \mu_X(t) = 0 \]

2. 再求自相关函数 $R_X(\tau) = E[X(t)X(t+\tau)]$

\[ \begin{aligned} R_X(\tau) &= E[X(t)X(t+\tau)] \\ &= E\left[ A\sin(t+\Theta) \cdot A\sin(t+\tau+\Theta) \right] \\ &= E[A^2] \cdot E_\Theta\left[ \sin(t+\Theta)\sin(t+\tau+\Theta) \right] \\ \end{aligned} \]

$A$ 在 $(-1,1)$ 上均匀分布，$E[A^2]=\int_{-1}^1 a^2 \cdot \frac12 da = \frac13$。
再看第二项 $E_\Theta\left[ \sin(t+\Theta)\sin(t+\tau+\Theta) \right]$

\[ \begin{aligned} &E_\Theta\left[ \sin(t+\Theta)\sin(t+\tau+\Theta) \right] \\ &= \frac12 \sin(t+\frac\pi4)\sin(t+\tau+\frac\pi4) + \frac12 \sin(t-\frac\pi4)\sin(t+\tau-\frac\pi4) \quad \text{诱导公式}\\ &= \frac12 \left[ \sin(t+\frac\pi4)\sin(t+\tau+\frac\pi4) + \cos(t+\frac\pi4)\cos(t+\tau+\frac\pi4) \right] \\ &= \frac12 \cos\tau \end{aligned} \]

因此

\[ R_X(\tau) = E[A^2] \cdot \frac12 \cos\tau = \frac13 \cdot \frac12 \cos\tau = \frac{1}{6} \cos\tau \]

3. 结论

均值为常数，自相关函数只与 $\tau$ 有关，与 $t$ 无关，所以 $\{X(t)\}$ 是宽平稳过程。

5.7¶

5.7

设 $\{B(t);t\geqslant0\}$ 是标准布朗运动 . 令 $X(t)=B(t+1)-B(t).$ (1) 计算$\{X(t);t\geqslant0\}$的均值函数和自相关函数，并写出详细过程； (2) 证明$\left\{X(t);t\geqslant0\right\}$是严平稳过程。

解：

(1) 计算均值函数和自相关函数

首先，$B(t)$ 是标准布朗运动，已知 $E[B(t)] = 0$，$Cov(B(s), B(t)) = \min(s, t)$。

计算均值函数： $$ mu_X(t) = E[X(t)] = E[B(t+1) - B(t)] = E[B(t+1)] - E[B(t)] = 0 - 0 = 0 $$

计算自相关函数 $R_X(\tau) = E[X(t) X(t+\tau)]$：

\[ \begin{aligned} R_X(\tau) &= E\left[(B(t+1) - B(t))(B(t+\tau+1) - B(t+\tau))\right] \\ &= E[B(t+1)B(t+\tau+1)] - E[B(t+1)B(t+\tau)] - E[B(t)B(t+\tau+1)] + E[B(t)B(t+\tau)] \\ &= \min(t+1, t+\tau+1) - \min(t+1, t+\tau) - \min(t, t+\tau+1) + \min(t, t+\tau)\\ &= t+1 - t - \min\{t+1,\, t+\tau\} + t \\ &= \begin{cases} 0, & \tau \geq 1 \\[1ex] 1 - \tau, & 0 \leq \tau < 1 \end{cases} \end{aligned} \]

(2) 证明 $\{X(t)\}$ 是严平稳过程

严平稳过程的定义：任意有限维分布在时间平移下不变。
由于 $B(t)$ 具有平稳独立增量，$X(t) = B(t+1) - B(t)$ 的分布与 $t$ 无关，且任意有限组 $\{X(t_1), X(t_2), ..., X(t_n)\}$ 的联合分布只与各自的时间间隔有关，与起始时刻无关。
因此，$\{X(t)\}$ 是严平稳过程。

5.12¶

5.12

设随机过程 $X(t) = \sqrt{2}X \cos t + Y \sin t,\ -\infty < t < \infty$，其中 $X, Y$ 相互独立，$X$ 的密度函数为

\[ f(x) = \begin{cases} 1 - |x|, & -1 < x < 1, \\ 0, & \text{其他}, \end{cases} \]

$Y$ 服从区间 $(-1, 1)$ 上的均匀分布。

(1) 求 $\mu_X(t)$, $R_X(t, t+\tau)$，并证明 $\{X(t); -\infty < t < \infty\}$ 是平稳过程；

(2) 求 $\{X(t)\}$ 的时间均值 $\langle X(t) \rangle$，并判断 $\{X(t); -\infty < t < \infty\}$ 的均值是否具有各态历经性；

(3) 判断 $\{X(t); -\infty < t < \infty\}$ 是否为各态历经过程。

解：

(1) 计算均值函数 $\mu_X(t)$ 和自相关函数 $R_X(t, t+\tau)$

首先计算 $E(X)$：

\[ \begin{align*} E(X) &= \int_{-1}^1 x(1 - |x|) dx \\ &= \int_0^1 x(1 - x) dx + \int_{-1}^0 x(1 + x) dx\\ &= \int_0^1 x dx - \int_0^1 x^2 dx + \int_{-1}^0 x dx + \int_{-1}^0 x^2 dx\\ &= \frac{1}{2} - \frac{1}{3} - \frac{1}{2} + \frac{1}{3} = 0 \end{align*} \]

因为 $Y$ 服从区间 $(-1, 1)$ 上的均匀分布，所以 $E(Y) = 0$。

因此，

\[ \begin{align*} \mu_X(t) &= E[X(t)]\\ &= \sqrt{2} \cos t \cdot E(X) + \sin t \cdot E(Y) \\ &= 0 \end{align*} \]

进一步计算方差和协方差：

\[ \begin{align*} E(X^2) &= \int_{-1}^1 x^2 (1 - |x|) dx = \frac{1}{6} \\ E(Y^2) &= \int_{-1}^1 y^2 \cdot \frac{1}{2} dy = \frac{1}{3} \\ E(XY) &= E(X)E(Y) = 0 \\ D(Y) &= E(Y^2) - [E(Y)]^2 = \frac{1}{3} \end{align*} \]

计算自相关函数：

\[ \begin{aligned} R_X(t, t+\tau) &= E[X(t) X(t+\tau)] \\ &= E\left[ (\sqrt{2} X \cos t + Y \sin t)(\sqrt{2} X \cos (t+\tau) + Y \sin (t+\tau)) \right] \\ &= 2 E(X^2) \cos t \cos (t+\tau) + E(Y^2) \sin t \sin (t+\tau) \\ &= \frac{1}{3} \cos t \cos (t+\tau) + \frac{1}{3} \sin t \sin (t+\tau) \\ &= \frac{1}{3} \cos \tau \end{aligned} \]

因此，$\{X(t)\}$ 是平稳过程。

(2) 计算时间均值 $\langle X(t) \rangle$ 并判断均值的各态历经性

\[ \begin{align*} \langle X(t) \rangle &= \lim_{T \rightarrow \infty} \frac{1}{2T} \int_{-T}^{T} X(t) dt\\ &= \lim_{T \rightarrow \infty} \frac{1}{2T} \int_{-T}^{T} (\sqrt{2} X \cos t + Y \sin t) dt\\ &= \lim_{T \rightarrow \infty} \frac{1}{2T} \left( 2\sqrt{2} X \sin T + 2Y \cos T \right) = 0 \end{align*} \]

所以

\[ \langle X(t) \rangle = E[X(t)] = 0 \]

因此，均值具有各态历经性。

(3) 判断是否为各态历经过程

计算二阶时间均值：

\[ \begin{align*} \langle X(t) X(t + \tau) \rangle &= \lim_{T \rightarrow \infty} \frac{1}{2T} \int_{-T}^{T} X(t) X(t + \tau) dt\\ &= \lim_{T \rightarrow \infty} \frac{1}{2T} \int_{-T}^{T} (\sqrt{2} X \cos t + Y \sin t)(\sqrt{2} X \cos (t + \tau) + Y \sin (t + \tau)) dt\\ &= (X^2 + \frac{Y^2}{2}) \cos^2 \tau \neq R_X(t, t + \tau) \end{align*} \]

因此，$\{X(t)\}$ 不是各态历经过程。

5.14¶

5.14

设 $\{N(t);t\geqslant0\}$ 是参数为 1 的泊松过程，$A$ 与 $\{N(t);t\geqslant0\}$ 独立，且 $A\sim U(0,1).$ 令 $X(t)=A[N(t+1)-N(t)].$ (1)计算$\{X(t);t\geqslant0\}$的均值函数和自相关函数； (2)证明$\{X(t);t\geqslant0\}$是宽平稳过程； (3)判断$\{X(t);t\geqslant0\}$的均值是否具有各态历经性，说明理由.

5.16¶

5.16

设 $X_1,X_2,\cdots$ 相互独立 $,E(X_i)=\mu,D(X_i)=\sigma^2>0.$ 令 $Y_n=X_nX_{n+1}X_{n+2}$ (1)计算$\{Y_n;n\geqslant1\}$的均值函数和自相关函数，并证明它是平稳过程； (2)计算时间均值$\langle Y_n\rangle.$

5.19¶

设平稳过程 $\{X(t); -\infty < t < \infty\}$ 的谱密度为 $S_{X}(\omega) = \frac{1}{\omega^{4} + 5\omega^{2} + 6}$, 求 $\{X(t)\}$ 的自相关函数

\[ S_{X}(\omega) = \frac{1}{\omega^{2}+2} - \frac{1}{\omega^{2}+3} \]

所以自相关函数为：

\[ R_{X}(\tau) = \frac{\sqrt{2}}{4} e^{-\sqrt{2}|\tau|} - \frac{\sqrt{3}}{6} e^{-\sqrt{3}|\tau|} \]

5.21¶

设 $X(t) = A \cos t + B \sin t + C$, $-\infty < t < \infty$，其中 $A, B, C$ 相互独立且同服从区间 $[-1, 1]$ 上的均匀分布。

(1) 证明 $\{X(t); -\infty < t < \infty\}$ 是平稳过程

\[ \begin{aligned} \mu_X &= E[X(t)] = E(A)\cos t + E(B)\sin t + E(C) = 0 \\ R_X(\tau) &= E[X(t)X(t+\tau)] \\ &= E\left[ (A\cos t + B\sin t + C)(A\cos(t+\tau) + B\sin(t+\tau) + C) \right] \\ &= E[A^2]\cos t\cos(t+\tau) + E[B^2]\sin t\sin(t+\tau) + E[C^2] \\ &= \frac{1}{3} \cos t\cos(t+\tau) + \frac{1}{3} \sin t\sin(t+\tau) + \frac{1}{3} \\ &= \frac{1}{3} \left[ \cos t\cos(t+\tau) + \sin t\sin(t+\tau) \right] + \frac{1}{3} \\ &= \frac{1}{3} \cos \tau + \frac{1}{3} \end{aligned} \]

即 $R_X(\tau)$ 只与时间差 $\tau$ 有关，$R_X(\tau) = \frac{1}{3}\cos(\tau) + \frac{1}{3}$，因此是平稳过程。

(2) 计算 $\langle X(t) \rangle$，判断均值是否具有各态历经性，并说明理由

\[ \begin{aligned} \langle X(t) \rangle &= \lim_{T\to\infty} \frac{1}{2T} \int_{-T}^{T} X(t) dt \\ &= \lim_{T\to\infty} \frac{1}{2T} \int_{-T}^{T} [A\cos t + B\sin t + C] dt \\ &= A \cdot 0 + B \cdot 0 + C \\ &= C \end{aligned} \]

由于 $C$ 是随机变量且 $E[C]=0$，但 $C$ 本身不恒等于 $0$，所以 $\mu_X \neq \langle X(t) \rangle$，均值不具有各态历经性。

(3) 求 $\{X(t)\}$ 的谱密度 $S_X(\omega)$

\[ \begin{aligned} R_X(\tau) &= \frac{1}{3}\cos(\tau) + \frac{1}{3} \\ S_X(\omega) &= \mathscr{F}[R_X(\tau)] \\ &= \frac{1}{3} \mathscr{F}[\cos\tau] + \frac{1}{3} \mathscr{F}[1] \\ &= \frac{1}{3} \pi [\delta(\omega-1) + \delta(\omega+1)] + \frac{1}{3} 2\pi \delta(\omega) \end{aligned} \]

5.22¶

已知平稳过程 $\{X(t); -\infty < t < \infty\}$ 的谱密度为

\[ S_X(\omega) = \begin{cases} 2\delta(\omega) + 1 - |\omega|, & |\omega| < 1, \\ 0, & \text{其他}, \end{cases} \]

求 $\{X(t)\}$ 的自相关函数

当 $|\omega| < 1$ 时，$S_X(\omega) = 2\delta(\omega) + 1 - |\omega|$。

\[ \begin{aligned} R_X(\omega)&=\frac{1}{2\pi}\int_{-1}^{1}e^{j\omega\tau}(2\delta(\omega)+1-|\omega|)d\omega\\ &= \frac{1}{2\pi}\int_{-\infty}^{+\infty}e^{j\omega\tau}2\delta(\omega)d\omega + \frac{1}{2\pi}\int_{0}^{1}e^{j\omega\tau}(1-\omega)d\omega + \frac{1}{2\pi}\int_{-1}^{0}e^{j\omega\tau}(1+\omega)d\omega\\ &= \frac{1}{\pi} + \frac{1}{2\pi}\int_{0}^{1}e^{j\omega\tau}(1-\omega)d\omega + \frac{1}{2\pi}\int_{0}^{1}e^{-j\omega\tau}(1-\omega)d\omega\\ &=\frac{1}{\pi}+\frac{1}{\pi}\int_0^1\cos\omega\tau(1-\omega)d\omega\\ &=\frac{1}{\pi}+\frac{1-\cos\tau}{\pi\tau^2} \end{aligned} \]

5.24¶

设 $\{X(t); -\infty < t < \infty\}$ 是均值为零的平稳过程 , $Y(t) = X(t)\cos(t+\Theta)$, 其中 $P(\Theta=\frac{\pi}{4})=P(\Theta=-\frac{\pi}{4})=0.5$, 且 $\{X(t)\}$ 与 $\Theta$ 相互独立 . 记 $\{X(t)\}$ 的自相关函数为 $R_X(\tau)$, 谱密度为 $S_X(\omega)$. 证明 :

(1) $\{Y(t); -\infty < t < \infty\}$ 是平稳过程 , 其自相关函数 $R_Y(\tau) = \frac{1}{2}R_X(\tau)\cos\tau$;

均值:

\[ \mu_X = E[Y(t)] = E[X(t)]E[\cos(t + \theta)] = 0 \]

自相关函数:

\[ \begin{aligned} R_Y(\tau) &= E[X(t)\cos(t + \theta) \cdot X(t + \tau)\cos(t + \tau + \theta)] \\ &= R_X(\tau) \, E[\cos(t + \theta)\cos(t + \tau + \theta)] \\ &=R_{x}(t)[\frac{1}{2}\cos(t+\frac{\pi}{4})\cos(t+t+\frac{\pi}{4})+\frac{1}{2}\cos(t-\frac{\pi}{4})\cos(t+t-\frac{\pi}{4})]\\ &=\frac{1}{2}R_{x}(t)\cos(\tau) \end{aligned} \]

(2) $\{Y(t)\}$ 的谱密度为 $S_Y(\omega) = \frac{1}{4}[S_X(\omega-1)+S_X(\omega+1)]$.

谱密度即傅里叶变换，利用傅立叶变换性质，有

$R_X(\tau)$ 的傅里叶变换为 $S_X(\omega)$
$\cos(\omega_0\tau)$ 的傅立叶变换是 $\pi[\delta(\omega-\omega_0)+\delta(\omega+\omega_0)]$

直接运算

当一个信号乘以余弦时，其频谱会产生频移（spectral shifting）：

\[ R_X(\tau)\cos(\omega_0 \tau) = \frac{1}{2}R_X(\tau) e^{j\omega_0 \tau} + \frac{1}{2}R_X(\tau) e^{-j\omega_0 \tau} \]

对上式做傅里叶变换（记为 $\mathcal{F} \{ \cdot \}$）：

\[ \mathcal{F} \{ R_X(\tau) \cos(\omega_0 \tau) \} = \frac{1}{2} S_X(\omega - \omega_0) + \frac{1}{2} S_X(\omega + \omega_0) \]

时域卷积对应频域相乘

\[ f(\tau)g(\tau) \rightarrow \frac{1}{2\pi} F(\omega) * G(\omega) \]

应用到当前情况：

\[ \begin{aligned} R_X(\tau)\cos(\omega_0 \tau) &\rightarrow{\mathcal{F}} \frac{1}{2\pi} S_X(\omega) * \pi[\delta(\omega - \omega_0) + \delta(\omega + \omega_0)]\\ &= \frac{1}{2} \left[S_X(\omega - \omega_0) + S_X(\omega + \omega_0)\right] \end{aligned} \]

5.25¶

设平稳过程 $\{X(t); -\infty < t < \infty\}$ 的谱密度为 $S_X(\omega)$，令 $Y(t) = X(t + L) - X(t)$，证明：$\{Y(t)\}$ 的谱密度为 $S_Y(\omega) = 2S_X(\omega)\left(1 - \cos \omega L\right).$

\[ R_Y(\tau) = 2R_X(\tau) - R_X(\tau + L) - R_X(\tau - L) \]

对其进行傅里叶变化，有

\[ S_Y(\omega) = \int_{-\infty}^{\infty} R_Y(\tau)e^{-j\omega\tau}d\tau \]

根据时移性质有：

\[ \int_{-\infty}^{\infty} R_X(\tau \pm L)e^{-j\omega\tau}d\tau = S_X(\omega)e^{\pm j\omega L} \]

因此：

\[ \begin{aligned} S_Y(\omega) &= S_X(\omega)(2 - (e^{j\omega L} + e^{-j\omega L}))\\ &= 2S_X(\omega)(1 - \cos L) \end{aligned} \]

时域	频域
\(e^{-a\mid\tau\mid}\)	\(\frac{2a}{a^2+\omega^2}\)
\(\frac{sin\omega_0\tau}{\pi\tau}\)	\(\begin{cases}1\quad\mid\omega\mid\leq\omega_0\\[2ex]0\quad\mid\omega\mid>\omega_0\end{cases}\)
\(1\)	\(2\pi\delta(\omega)\)
\(\delta(\tau)\)	\(1\)
\(cos\omega_0\tau\)	\(\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]\)

时域	频域
\(e^{-a\mid\tau\mid}\)	\(\frac{2a}{a^2+\omega^2}\)
\(\begin{cases}1-\frac{\mid\tau\mid}{T}\quad\mid\tau\mid\leq T\\[2ex]0\quad\mid\tau\mid>T\end{cases}\)	\((\frac{sin(\omega T/2)}{\omega T/2})^2\)
\(\frac{sin\omega_0\tau}{\pi\tau}\)	\(\begin{cases}1\quad\mid\omega\mid\leq\omega_0\\[2ex]0\quad\mid\omega\mid>\omega_0\end{cases}\)
\(1\)	\(2\pi\delta(\omega)\)
\(\delta(\tau)\)	\(1\)
\(cos\omega_0\tau\)	\(\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]\)
\(R_X(\tau)cos\omega_0\tau\)	\(\frac12[S_X(\omega+\omega_0)+S_X(\omega-\omega_0)]\)