信息论 ¶

约 2112 个字 1 张图片预计阅读时间 8 分钟

信息论简介

信息论的发展历史
信息论的应用领域

信息的度量 ¶

熵：系统自身的不确定性。
KL 散度：两个分布的差异，衡量“错误假设的代价”。
交叉熵：实际中常用的“训练信号”，等价于熵 + KL，核心就是让预测分布 $Q$ 逼近真实分布 $P$。

信息量的定义（自信息）¶

单个事件的信息量（自信息）定义为：

\[ I(x) = -\log p(x) \]

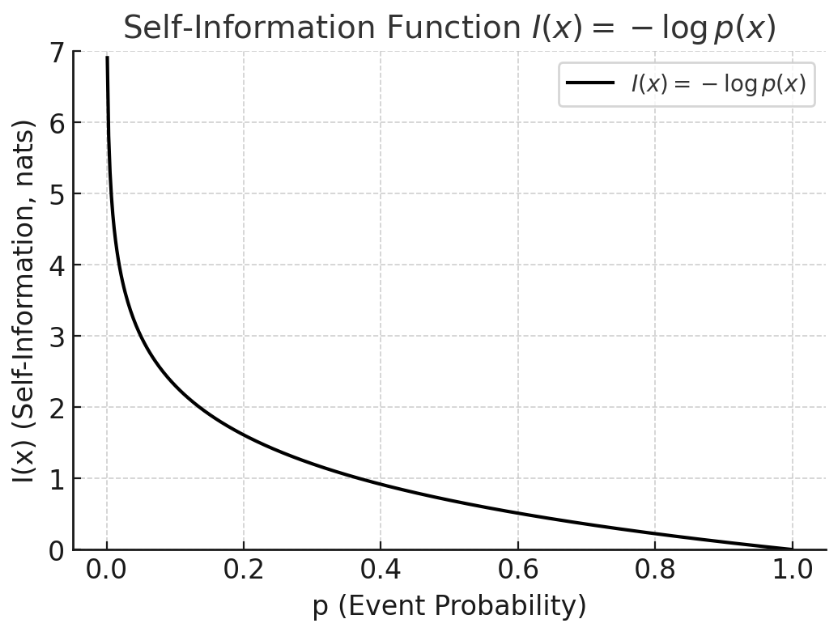
性质

罕见事件 → 信息量大：若 $p(x)$ 很小，说明事件罕见，那么 $I(x)$ 很大。
必然事件 → 信息量为零：若 $p(x)=1$，则 $I(x)=0$，不包含任何新信息。
可加性：如果两个事件独立，则信息量相加。

含义

可以理解为“看到某事件的惊讶程度”，不确定度更大，则信息量更大
也可以理解为“事件消除了多少不确定性”。
不确定 -》确定的难度

例子

掷硬币，结果是“正面”。概率 $p=0.5$。

$$ I = -log_2(0.5) = 1 text{比特} $$ * 掷骰子，结果是“6”。概率 $p=1/6$。

\[ I = -\log_2(1/6) \approx 2.585 \ \text{比特} \]

说明掷骰子的结果比掷硬币单次结果包含更多信息。

为什么使用 log

熵是服从某一特定概率分布事件的理论最小平均编码长度

那么从二进制的角度思考，如果一个事件发生的概率是 $p$，那么我们需要用 $-\log_2(p)$ 个比特来编码这个事件。

信息熵（Shannon Entropy）¶

对于离散分布 $P(X)$，熵定义为：

\[ H(P) = - \sum_{x} P(x) \log P(x) = \mathbb{E}[-\log P(x)] \]

从公式中可以看出，信息熵就是自信息的期望，也就是平均信息量

性质

非负性：$H(P) \geq 0$。
加法性：独立变量的联合熵等于熵的和。
最大熵分布 在不同的约束条件下，最大熵分布不同。
- 均匀分布是最大熵分布
- 一二阶矩确定的情况下，正态分布是最大熵分布（为什么大量生活中会看到的随机事件分布都服从正态分布呢？说明大自然有着创造最大惊喜的倾向，或者说，就是要让你猜不透。这也是理解热力学中的熵增定律的另一个角度）

为什么熵在均匀分布时最大

椎名 - 知乎

考虑支集为 $[a,b]$ 的密度函数 , 即在约束条件

\[ \int_{a}^{b} p(x) \, \mathrm{d}x = 1 \]

下极大化 $H(p)$. 考虑 Lagrange 函数

\[ J(p) = -\int_{a}^{b} p(x) \log p(x) \, \mathrm{d}x + \lambda \left( \int_{a}^{b} p(x) \, \mathrm{d}x - 1 \right) \]

求 functional derivative, 得

\[ \frac{\delta J(p)}{\delta p} = -\log p - 1 + \lambda \]

令上式等于 0, 可得

\[ p(x) = \mathrm{e}^{\lambda-1} \]

再由约束条件即得 $p(x) = \frac{1}{b-a} \mathbf{1}_{[a,b]}(x)$.

独立变量的联合熵等于熵的和

设有两个随机变量 $X, Y$。

联合熵定义：

\[ H(X, Y) = - \sum_{x,y} p(x,y) \log p(x,y) \]

如果独立，则 $p(x,y) = p(x) p(y)$。代入：

\[ \begin{aligned} H(X,Y) &= - \sum_{x,y} p(x)p(y) \log \big(p(x)p(y)\big)\\ &= - \sum_{x,y} p(x)p(y) [\log p(x) + \log p(y)]\\ &= - \sum_{x} p(x) \log p(x) \sum_y p(y) - \sum_y p(y) \log p(y) \sum_x p(x) \end{aligned} \]

$\because \sum_x p(x) = \sum_y p(y) = 1$

\[ H(X,Y) = H(X) + H(Y) \]

所以 独立随机变量的联合熵等于各自熵的和。

如果不独立，则会出现“冗余”，不确定性减少，故 $H(X,Y) < H(X)+H(Y)$。

物理与现实含义

熵刻画 不确定性 或 信息量的平均值。
在通信中，熵就是编码所需的平均比特数。

形象化理解

如果一个骰子是公平的，结果完全不可预测 → 熵高。
如果一个骰子是“永远掷出 6”，完全确定 → 熵为零。
可以理解为 “消息的惊讶程度的平均值”。

在深度学习中的作用

熵常用于正则化或信息瓶颈（如 VAEs）。
在强化学习中，用策略熵来保持探索。

联合熵 ¶

公式

对于两个随机变量 $X, Y$：

\[ H(X, Y) = - \sum_{x,y} p(x,y) \log p(x,y) \]

含义

表示同时观察两个随机变量所需的平均信息量。
可以理解为 系统整体的不确定性。

例子

两个独立硬币同时抛掷：每个硬币熵 $=1$ 比特，联合熵 $= 1+1 = 2$ 比特。
如果两个硬币是“完全同步”的（总是一致），则联合熵 = 1，比单个硬币大不了多少。

条件熵 ¶

公式

\[ H(Y|X) = - \sum_{x,y} p(x,y) \log p(y|x) \]

含义

表示 在已知 X 的情况下，Y 仍然有多少不确定性。
直观理解：知道了 $X$，还需要多少信息来确定 $Y$。

关系式

\[ H(X,Y) = H(X) + H(Y|X) = H(Y) + H(X|Y) \]

例子

掷两个硬币，彼此独立： $H(Y|X) = H(Y)$，因为知道一个硬币的结果，对另一个没有帮助。
掷两个“完全同步”的硬币： $H(Y|X) = 0$，因为知道 $X$，就能完全确定 $Y$。

互信息（Mutual Information）¶

公式

有两种常见写法：

\[ I(X;Y) = \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)p(y)} \]

或

\[ I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) \]

性质

非负性：$I(X;Y) \geq 0$。
对称性：$I(X;Y) = I(Y;X)$。
取值范围：$0 \leq I(X;Y) \leq \min(H(X), H(Y))$。

含义

衡量两个变量 共享的信息量，即：知道 $X$ 能减少多少对 $Y$ 的不确定性。
如果独立，$I(X;Y)=0$。
如果完全相关，互信息等于熵本身。

形象化理解

可以用 熵的维恩图 来理解：
- 圆圈面积 = 熵。
- 重叠部分 = 互信息。
- 不重叠的部分 = 条件熵。

相对熵（Kullback-Leibler 散度）¶

Acknowledgement

关于 KL 散度（Kullback-Leibler Divergence）的笔记 - 捡到一束光 - 知乎

对于两个分布 $P$ 和 $Q$：

\[ D_{KL}(P \parallel Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)} \]

性质

非负性：$D_{KL}(P \parallel Q) \geq 0$，等号成立当且仅当 $P=Q$。
非对易性：$D_{KL}(P \parallel Q) \neq D_{KL}(Q \parallel P)$
本质是一个“距离”，但不是严格的度量。

非负性证明

这是因为 Gibbs 不等式 (Gibbs' inequality)。

\[ D_{KL}(P \parallel Q) = \mathbb{E}_{x \sim P} \left[\log \frac{P(x)}{Q(x)}\right] \]

注意到 $\log$ 是凹函数，应用 Jensen 不等式：

\[ \mathbb{E}_{x \sim P} \left[\log \frac{Q(x)}{P(x)}\right] \leq \log \mathbb{E}_{x \sim P} \left[\frac{Q(x)}{P(x)}\right] \]

右边的期望值为：

\[ \mathbb{E}_{x \sim P} \left[\frac{Q(x)}{P(x)}\right] = \sum_{x} P(x) \frac{Q(x)}{P(x)} = \sum_{x} Q(x) = 1 \]

所以：

\[ \mathbb{E}_{x \sim P} \left[\log \frac{Q(x)}{P(x)}\right] \leq \log 1 = 0 \]

取负号就得到：

\[ D_{KL}(P \parallel Q) \geq 0 \]

且当且仅当 $P(x) = Q(x)$ 对所有 $x$ 都成立时，KL 散度等于 0。

物理与现实含义

它的作用是：在模型训练中，我们利用 $Q(x)$ 来“逼近”真实分布 $P(x)$，而 KL 散度正是用来量化这种逼近的程度。
相当于问：如果真实世界服从 $P$，但我们却假设是 $Q$，会多付出多少信息代价？
KL 散度的理论意义在于度量两个概率分布之间的差异程度，当 KL 散度越大的时候，说明两者的差异程度越大；而当 KL 散度小的时候，则说明两者的差异程度小。如果两者相同的话，则该 KL 散度应该为 0。

形象化理解

想象你要压缩一串消息，真实分布是 $P$，但你用错误的模型 $Q$ 来编码 → 结果会多用额外的比特。
这个“额外成本”就是 KL 散度。

为什么是 $P(x) \log \frac{P(x)}{Q(x)}$

我们先简单回顾一下信息量的概念。信息量衡量的是，某个事件发生时带来的“惊讶感”，也就是说，信息量越大，说明事件发生的不确定性越高。

事件使用 $Q(x)$ 描述的时候，带来的信息量是 $-\log Q(x)$，那么使用 $P(x)$ 描述的时候，带来的信息量是 $-\log P(x)$，那么使用 $Q(x)$ 描述的时候，带来的信息损失是 $-\log Q(x) - (-\log P(x)) = \log \frac{P(x)}{Q(x)}$。而使用 $P(x)$ 求期望的原因是，我们关心的分布是 $P(x)$，所以需要用 $P(x)$ 的期望来表示。

KL 散度本质上是在计算，用 $Q(x)$ 来代替真实的 $P(x)$ 时，带来的信息损失。换句话说，KL 散度告诉你真实分布和模型预测分布之间的差距

为什么不是 $P(x) \log P(x) - Q(x) \log Q(x)$？

这个表达式看似很直观，但它实际上没有反映出我们想要计算的“信息损失”。它只是分别计算了两个分布的信息量，并没有量化两者之间的差异。

KL 散度的目的是计算用模型 $Q(x)$ 来描述真实分布 $P(x)$ 的损失，而不是计算它们各自的“信息量”。所以，公式必须是 $P(x) \log \frac{P(x)}{Q(x)}$，因为它直接度量了两者之间的差异。

交叉熵 (Cross Entropy) ¶

˜

Acknowledgement

我们可以把交叉熵想象为“主观概率为 $Q$ 的观察者在看到根据概率 $P$ 生成的数据时的预期惊异”。

（i）最大化观测数据的似然；（ii）最小化传达标签所需的惊异。

交叉熵定义为：

\[ H(P, Q) = - \sum_{x} P(x) \log Q(x) \]

并且有关系：

\[ H(P, Q) = H(P) + D_{KL}(P \parallel Q) \]

性质

总是大于等于熵：$H(P, Q) \geq H(P)$。
等号成立当且仅当 $P=Q$。
是最常用的分类损失函数。

物理与现实含义

表示用分布 $Q$ 来编码真实分布 $P$ 的平均编码长度。
与 KL 散度联系紧密：交叉熵 = 真实不确定性 ( 熵 ) + 额外代价 (KL)。

形象化理解

对于概率，比较经典的理解是看做是重复试验无限次后事件频率会逼近的值，是一个客观存在的值；但是贝叶斯学派提出了另一种理解方式：即将概率理解为我们主观上对事件发生的确信程度。

两种理解其实在逻辑上似乎并不互斥，既可以有客观存在，也可以有主观认识，所以我们不妨假设：

针对同一个随机变量空间有两个分布，分别记作 $p_{0}$ 和 $p_{s}$ ；

$p_{s}(x)$ 是我们主观认为 $x$ 会发生的概率，下标 s 代表 subjective；

$p_{o}(x)$ 是客观上 $x$ 会发生的概率，下标 o 代表 objective。

这种情况下，客观上这个随机事件 $X$ 会给我们造成惊喜的期望应该是：

\[ H_{p_{o},p_{s}}(X) = \int p_{o}(x) \log \frac{1}{p_{s}(x)} dx \]

再翻译一下，交叉熵是什么？可以理解为：

我们带着某个主观认知去接触某个客观随机现象的时候，会产生的平均惊喜度。（因为要用客观随机现象，所以使用的是 $=p_0(x)$）

那什么时候交叉熵（也就是我们会获得的平均惊喜度）会大？就是当我们主观上认为一个事情发生的概率很低（$1/p_{s}(x)$ 很大），但是客观上发生概率很高（$p_{o}(x)$ 很大）的时候，也就是主观认知和客观现实非常不匹配的时候。机器学习当中为啥用交叉熵来当作损失函数应该也就不言自明了。

信息论 ¶

信息的度量 ¶

信息量的定义（自信息）¶

信息熵（Shannon Entropy）¶

联合熵 ¶

条件熵 ¶

互信息（Mutual Information）¶

相对熵（Kullback-Leibler 散度）¶

交叉熵 (Cross Entropy) ¶

信源编码 ¶

信道与信道容量 ¶

纠错编码 ¶

信息论在机器学习中的应用 ¶

特征选择中的信息增益 ¶

决策树与信息熵 ¶

变分自编码器中的 KL 散度 ¶

信息论与数据压缩 ¶

信息论与密码学 ¶