02 | 微分与积分 ¶
约 1857 个字 1 张图片 预计阅读时间 7 分钟
变元与函数 ¶
\(\boldsymbol{x}=[x_1,\cdots,x_m]^{\mathrm{T}}\in\mathbb{R}^m\) 为实向量变元；
\(\boldsymbol{X}=[\boldsymbol{x}_1,\cdots,\boldsymbol{x}_n]\in\mathbb{R}^{m\times n}\) 为实矩阵变元；
根据输入输出的类型不同，我们可以把函数分为以下几种：
| 输入输出 | 输入为向量 \(\boldsymbol{x}\in\mathbb{R}^m\) | 输入为矩阵 \(\boldsymbol{X}\in\mathbb{R}^{m\times n}\) |
|---|---|---|
| 标量输出 | \(f(\boldsymbol{x})\in\mathbb{R}\)，记作 \(f:\mathbb{R}^m\to\mathbb{R}\) 例：向量的范数 |
\(f(\boldsymbol{X})\in\mathbb{R}\)，记作 \(f:\mathbb{R}^{m\times n}\to\mathbb{R}\) 例：矩阵的迹 |
| 向量输出 | \(f(\boldsymbol{x})\in\mathbb{R}^p\)，记作 \(f:\mathbb{R}^m\to\mathbb{R}^p\) 例：卷积、傅立叶变换 |
\(f(\boldsymbol{X})\in\mathbb{R}^p\)，记作 \(f:\mathbb{R}^{m\times n}\to\mathbb{R}^p\) |
| 矩阵输出 | \(\boldsymbol{F}(\boldsymbol{x})\in\mathbb{R}^{p\times q}\)，记作 \(\boldsymbol{F}:\mathbb{R}^m\to\mathbb{R}^{p\times q}\) 例：vandermonde 矩阵、confusion matrix |
\(\boldsymbol{F}(\boldsymbol{X})\in\mathbb{R}^{p\times q}\)，记作 \(\boldsymbol{F}:\mathbb{R}^{m\times n}\to\mathbb{R}^{p\times q}\) 例：输入是猫狗图，输出是猫狗分类结果 |
微分与积分：element-wise
\[
\frac{\mathrm{d} \mathbf{A}}{\mathrm{d} t} = \mathbf{\dot{A}} = \begin{bmatrix} \frac{\mathrm{d} a_{11}}{\mathrm{d} t} & \frac{\mathrm{d} a_{12}}{\mathrm{d} t} & \cdots & \frac{\mathrm{d} a_{1n}}{\mathrm{d} t} \\ \frac{\mathrm{d} a_{21}}{\mathrm{d} t} & \frac{\mathrm{d} a_{22}}{\mathrm{d} t} & \cdots & \frac{\mathrm{d} a_{2n}}{\mathrm{d} t} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\mathrm{d} a_{m1}}{\mathrm{d} t} & \frac{\mathrm{d} a_{m2}}{\mathrm{d} t} & \cdots & \frac{\mathrm{d} a_{mn}}{\mathrm{d} t} \end{bmatrix}
\]
\[
\int \mathbf{A} \mathrm{d} t = \begin{bmatrix} \int a_{11} \mathrm{d} t & \int a_{12} \mathrm{d} t & \cdots & \int a_{1n} \mathrm{d} t \\ \int a_{21} \mathrm{d} t & \int a_{22} \mathrm{d} t & \cdots & \int a_{2n} \mathrm{d} t \\ \vdots & \vdots & \ddots & \vdots \\ \int a_{m1} \mathrm{d} t & \int a_{m2} \mathrm{d} t & \cdots & \int a_{mn} \mathrm{d} t \end{bmatrix}
\]
矩阵求导的链式法则
\[
\frac{\mathrm{d}}{\mathrm{d} t} (\mathbf{A} \mathbf{B}) = \frac{\mathrm{d} \mathbf{A}}{\mathrm{d} t} \mathbf{B} + \mathbf{A} \frac{\mathrm{d} \mathbf{B}}{\mathrm{d} t}
\]
偏导 ¶
行偏导 - Jacobian Matrix ¶
行偏导算子
\[
\begin{align*}
\mathrm{D}_{x}&\overset{\mathrm{def}}{\operatorname*{=}}\frac{\partial}{\partial {x^{\mathrm{T}}}_{1\times m}}=\left[\frac{\partial}{\partial x_{1}},\cdots,\frac{\partial}{\partial x_{m}}\right]_{1\times m}\\
\mathrm{D}_{\boldsymbol{x}}f(\boldsymbol{x})&=\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}^{\mathrm{T}}}=\left[\frac{\partial f(\boldsymbol{x})}{\partial x_{1}},\cdots,\frac{\partial f(\boldsymbol{x})}{\partial x_{m}}\right]
\end{align*}
\]
行偏导
\[
\begin{aligned}
f(x)&=x^{T}x\\
D_{x}f(x)&=\frac{\partial f(x)}{\partial x^{T}}=[\frac{\partial f(x)}{\partial x_{1}}\cdots\frac{\partial f(x)}{\partial x_{m}}]\\
&=[\frac{\partial x^{T}x}{\partial x_{1}}\cdots\frac{\partial x^{T}x}{\partial x_{m}}]\\
&=[2x_{1}\cdots2x_{m}]=2x^{T}\end{aligned}
\]
如果变元是矩阵，也可以写出行偏导
\[
\begin{aligned}
&\mathrm{D}_{\mathrm{vec}\boldsymbol{X}}f(\boldsymbol{X})=\frac{\partial f(\boldsymbol{X})}{\partial\mathrm{vec}^{\mathrm{T}}(\boldsymbol{X})}=\left[\frac{\partial f(\boldsymbol{X})}{\partial x_{11}},\cdots,\frac{\partial f(\boldsymbol{X})}{\partial x_{m1}},\cdots,\frac{\partial f(\boldsymbol{X})}{\partial x_{1n}},\cdots,\frac{\partial f(\boldsymbol{X})}{\partial x_{mn}}\right]_{1\times mn}\\
&\mathrm{D}_{\mathrm{vec}\boldsymbol{X}}f(\boldsymbol{X})=\mathrm{rvec}(\mathrm{D}_{\boldsymbol{X}}f(\boldsymbol{X}))=\left(\mathrm{vec}(\mathrm{D}_{\boldsymbol{X}}^{\mathbf{T}}f(\boldsymbol{X}))\right)^{\mathbf{T}}
\end{aligned}
\]
所以求行偏导的结果相当于把雅可比矩阵给行向量化了
\(f(X)\) 关于矩阵变元 \(X\) 的 Jacobian 矩阵
\(X \in \mathbb{R}^{m \times n}\)
\[
D_X f(X) = \frac{\partial f(X)}{\partial X^T} = \begin{bmatrix} \frac{\partial f(X)}{\partial x_{11}} & \ldots & \frac{\partial f(X)}{\partial x_{m1}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f(X)}{\partial x_{1n}} & \ldots & \frac{\partial f(X)}{\partial x_{mn}} \end{bmatrix} \in \mathbb{R}^{n \times m}
\]
\[
\mathrm{D}_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X})\overset{\mathrm{def}}{\operatorname*{=}}\frac{\partial\mathrm{vec}(\boldsymbol{F}(\boldsymbol{X}))}{\partial(\mathrm{vec}\boldsymbol{X})^{\mathrm{T}}}\in\mathbb{R}^{pq\times mn}
\]
思路：
- 把矩阵函数列向量化 \(vec(\mathbf{F}(\mathbf{X})) =vec\begin{bmatrix}\mathbf{F}_{1} & \mathbf{F}_{2} & \cdots & \mathbf{F}_{q} \end{bmatrix}\)
- 列向量化之后，相当于把矩阵函数的每一个元素展开成了一个列向量，然后相当于标量对于矩阵求行偏导
\[
\begin{aligned}
&\mathrm{D}_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X})=\begin{bmatrix}\frac{\partial f_{11}}{\partial(vecX)^{\mathrm{T}}}\\\vdots\\\frac{\partial f_{p1}}{\partial(vecX)^{\mathrm{T}}}\\\vdots\\\frac{\partial f_{1q}}{\partial(vecX)^{\mathrm{T}}}\\\vdots\\\frac{\partial f_{pq}}{\partial(vecX)^{\mathrm{T}}}\end{bmatrix}
=\begin{bmatrix}\frac{\partial f_{11}}{\partial x_{11}}&\cdots&\frac{\partial f_{11}}{\partial x_{m1}}&\cdots&\frac{\partial f_{11}}{\partial x_{1n}}&\cdots&\frac{\partial f_{11}}{\partial x_{mn}}\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\\frac{\partial f_{p1}}{\partial x_{11}}&\cdots&\frac{\partial f_{p1}}{\partial x_{m1}}&\cdots&\frac{\partial f_{p1}}{\partial x_{1n}}&\cdots&\frac{\partial f_{p1}}{\partial x_{mn}}\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\\frac{\partial f_{1q}}{\partial x_{11}}&\cdots&\frac{\partial f_{1q}}{\partial x_{m1}}&\cdots&\frac{\partial f_{1q}}{\partial x_{1n}}&\cdots&\frac{\partial f_{1q}}{\partial x_{mn}}\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\\frac{\partial f_{pq}}{\partial x_{11}}&\cdots&\frac{\partial f_{pq}}{\partial x_{m1}}&\cdots&\frac{\partial f_{pq}}{\partial x_{1n}}&\cdots&\frac{\partial f_{pq}}{\partial x_{mn}}\end{bmatrix}
\end{aligned}
\]
列偏导 - Derivative 梯度 ¶
\(m\times1\) 列向量偏导算子即梯度算子记作 \(\nabla_{\boldsymbol{x}}\), 定义为
taking derivative with respect to a column vector
具有连续偏导→可微→有切平面→切线都在切平面上→有一个斜率最大的
\[
\nabla_{x}\stackrel{\mathrm{def}}{=}\frac{\partial}{\partial x_{m\times1}}=\left[\frac{\partial}{\partial x_{1}},\cdots,\frac{\partial}{\partial x_{m}}\right]^{\mathrm{T}}
\]
\[
\nabla_{\boldsymbol{x}}f(\boldsymbol{x})\stackrel{\mathrm{def}}{=}\left[\frac{\partial f(\boldsymbol{x})}{\partial x_{1}},\cdots,\frac{\partial f(\boldsymbol{x})}{\partial x_{m}}\right]^{\mathrm{T}}=\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}}
\]
\[
\nabla_{\boldsymbol{X}}f(\boldsymbol{X})=\begin{bmatrix}\frac{\partial f(\boldsymbol{X})}{\partial x_{11}}&\cdots&\frac{\partial f(\boldsymbol{X})}{\partial x_{1n}}\\\vdots&\ddots&\vdots\\\frac{\partial f(\boldsymbol{X})}{\partial x_{m1}}&\cdots&\frac{\partial f(\boldsymbol{X})}{\partial x_{mn}}\end{bmatrix}=\frac{\partial f(\boldsymbol{X})}{\partial\boldsymbol{X}}
\]
梯度矩阵是雅可比矩阵的转置
方向导数是一个数，梯度是一个向量
方向导数¶
方向导数是函数在某一特定方向上的变化率。它表示函数在定义域内某一点沿着给定方向的变化趋势。具体来说，对于一个具有定义域的函数 \(f(x, y)\)，在点 \((x_0, y_0)\) 处沿着方向向量
\[
D_{\vec{u}}f(x_0, y_0) = \lim_{h \to 0} \frac{f(x_0 + hu_1, y_0 + hu_2) - f(x_0, y_0)}{h}
\]
其中，\(h\) 是一个很小的正数，\(u_1\) 和 \(u_2\) 是方向向量 \(\vec{u}\) 的分量。
求导
\[
f(x) = x^{T}x = \sum_{i=1}^{n}x_{i}^{2}
\]
\[
\nabla_{x}f(x) = \begin{bmatrix} \frac{\partial \sum_{i=1}^{n}x_{i}^{2}}{\partial x_{1}} \\ \vdots \\ \frac{\partial \sum_{i=1}^{n}x_{i}^{2}}{\partial x_{n}} \end{bmatrix} = \begin{bmatrix} 2x_{1} \\ \vdots \\ 2x_{n} \end{bmatrix} = 2x
\]
很多时候低维推到高维的时候，结构是类似的，所以高维求不出来的时候，可以先从低维开始推，然后推广到高维
- 梯度的方向：函数上升最快的方向
- 梯度流：函数下降最快的方向，梯度方向的负方向 \(-\nabla_{\boldsymbol{x}}f(\boldsymbol{x})\) 称为函数 \(f\) 在点 \(\boldsymbol{x}\) 的梯度流 (gradient flow)，记作
\[
\dot{\boldsymbol{x}}=-\nabla_{\boldsymbol{x}}f(\boldsymbol{x}) \quad \text { 或 } \quad \dot{\boldsymbol{X}}=-\nabla_{\operatorname{vec} \boldsymbol{X}}f(\boldsymbol{X})
\]
梯度流是函数下降最快的方向
根据泰勒公式
\[
f(x+d) \approx f(x) + \nabla x^T f(x) d
\]
如果想让函数值下降 \(f(x+d)<f(x)\)
则需要 \(d\) 和 \(\nabla x^T f(x)\) 夹角大于 90 度，即 \(\cos \langle \nabla x^T f(x), d \rangle < 0\)，而其中
\[
-1 \leq \cos \langle \nabla x^T f(x), d \rangle = \frac{\nabla x^T f(x) d}{||\nabla x^T f(x)|| ||d||} \leq 1
\]
当只有 \(d\) 和 \(\nabla x^T f(x)\) 方向完全相反时，\(\cos \langle \nabla x^T f(x), d \rangle = -1\)，这个时候下降的速度最快
计算法则 - 核心链式法则 ¶
特例
特例：\(y \in R^{m\times 1}\), \(\mathbf{A} \in R^{m\times m}\)
- \(\frac{\partial{\mathbf{A}\mathbf{X}}}{\partial{\mathbf{X}}} = \mathbf{A}^T\)
- \(\frac{\partial{\mathbf{X}^T\mathbf{A}\mathbf{X}}}{\partial{\mathbf{X}}} = \mathbf{A}^T\mathbf{X} + \mathbf{AX}\)
- 若 \(f(X)=c\) 为常数，其中 \(X\) 为 \(m\times n\) 矩阵，则梯度 \(\frac{\partial c}{\partial X}= O_{m\times n}\)
- 线性法则：若 \(f(\boldsymbol{X})\) 和 \(g(\boldsymbol{X})\) 分别是矩阵 \(X\) 的实值函数，\(c_1\) 和 \(c_2\) 为实常数，则
$$ frac{partial[c_1f(boldsymbol{X})+c_2g(boldsymbol{X})]}{partialboldsymbol{X}}=c_1frac{partial f(boldsymbol{X})}{partialboldsymbol{X}}+c_2frac{partial g(boldsymbol{X})}{partialboldsymbol{X}} $$
- 乘积法则：若 \(f(X)\)、\(g(X)\) 和 \(h(X)\) 都是矩阵 \(X\) 的实值函数，则
$$ frac{partial[f(X)g(X)]}{partial X}=g(X)frac{partial f(X)}{partial X}+f(X)frac{partial g(X)}{partial X} $$
$$ frac{partial[f(X)g(X)h(X)]}{partial X}=g(X)h(X)frac{partial f(X)}{partial X}+f(X)h(X)frac{partial g(X)}{partial X}+f(X)g(X)frac{partial h(X)}{partial X} $$
- 链式法则：
$$ frac{partial g(f(boldsymbol X))}{partialboldsymbol X}=frac{mathrm{d}g(y)}{mathrm{d}y}frac{partial f(boldsymbol X)}{partialboldsymbol X} $$
独立性基本假设 ¶
假定实值函数的向量变元 \(\boldsymbol{x}=[x_{i}]_{i=1}^{m}\in\mathbb{R}^{m}\) 或者矩阵变元 \(\boldsymbol{X}=[x_{ij}]_{i=1,j=1}^{m,n}\in\mathbb{R}^{m\times n}\) 本身无任何特殊结构 , 即向量或矩阵变元的元素之间是各自独立的。
\[
\frac{\partial x_{i}}{\partial x_{j}}=\delta_{ij}=\begin{cases}1, & i=j \\ 0, & \text { 其他 }\end{cases}
\]
以及
\[
\frac{\partial x_{kl}}{\partial x_{ij}}=\delta_{ki}\delta_{lj}=\begin{cases}1, & k=i \text { 且 } l=j \\ 0, & \text { 其他 }\end{cases}
\]
其中 \(\delta_{ij}\) 是 Kronecker 符号
求实值函数 \(f(x)=x^{T}Ax\) 的 Jacobian 矩阵
由于 \(x^{T}Ax=\sum_{k=1}^{n}\sum_{l=1}^{n}a_{kl}x_{k}x_{l}\)
求出行偏导向量 \(\frac{\partial x^{T}Ax}{\partial x^{T}}\) 的第 \(i\) 个分量为
\[
[\frac{\partial x^{T}Ax}{\partial x^{T}}]_{i}=\frac{\partial}{\partial x_{i}}\sum_{k=1}^{n}\sum_{l=1}^{n}a_{kl}x_{k}x_{l}=\sum_{k=1}^{n}x_{k}a_{ki}+\sum_{l=1}^{n}x_{l}a_{il}
\]
先固定一个值，利用上面的独立性假设，可以求得
令 \(F(X) = X \in \mathbb{R}^{m \times n}\)，则直接计算偏导得
\[
\frac{\partial f_{kl}}{\partial x_{ij}} = \frac{\partial x_{kl}}{\partial x_{ij}} = \delta_{lj} \delta_{ki}
\]
于是得 Jacobian 矩阵
\[
\mathrm{D}_{X} F(X) \stackrel{\text { def }}{=} \frac{\partial \text{vec}(F(X))}{\partial(\text{vec} X)^{T}} \\ \mathrm{D}_{X} X = I_{n} \otimes I_{m} = I_{mn} \in \mathbb{R}^{mn \times mn}
\]
微分 ¶
一些规则 ¶
- 标量函数
$$ mathrm{d}[mathrm{tr}(mathbf{U})] = mathrm{d}left(sum_{i=1}^{n} u_{ii}right) = sum_{i=1}^{n} mathrm{d}u_{ii} = mathrm{tr}left(mathrm{d}mathbf{U}right) $$
- 矩阵乘积 UV 的微分矩阵
$$ mathrm{d}(mathbf{U}mathbf{V}) = (mathrm{d}mathbf{U})mathbf{V} + mathbf{U}(mathrm{d}mathbf{V}) $$
- 矩阵的迹的矩阵微分等于矩阵微分的迹
$$ mathrm{d}left(mathrm{tr}(mathbf{X})right) = mathrm{tr}(mathrm{d}mathbf{X}) $$
- 矩阵转置的微分等于矩阵微分的转置
$$ mathrm{d}(boldsymbol{X}^T) = (mathrm{d}boldsymbol{X})^T $$
- 矩阵线性组合的微分等于矩阵微分的线性组合
$$ mathrm{d}(alphaboldsymbol{X}+betaboldsymbol{Y}) = alphamathrm{d}boldsymbol{X}+betamathrm{d}boldsymbol{Y} $$
Jocabian 矩阵辨识 ¶
矩阵微分用符号 dX 表示
更方便得到雅可比矩阵
微分法则：
对于标量函数 \(f(\mathbf{x})\)，其中 \(\mathbf{x}=[x_1,x_2,\ldots,x_m]^T \in \mathbb{R}^m\)：
\[
\begin{aligned}
df(\mathbf{x}) = & \left[\frac{\partial f(\mathbf{x})}{\partial x_1},\ldots,\frac{\partial f(\mathbf{x})}{\partial x_m}\right]
\begin{bmatrix}
dx_1 \\ \vdots \\ dx_m
\end{bmatrix} \\
= & \frac{\partial f(\mathbf{x})}{\partial\mathbf{x}^T}d\mathbf{x} \\
= & \text{tr}(\boldsymbol{A}d\mathbf{x})
\end{aligned}
\]
对于标量函数 \(f(\boldsymbol{X})\)，其中 \(\boldsymbol{X} \in \mathbb{R}^{m\times n}\)：
\[
df(\boldsymbol{X}) = \text{tr}(\boldsymbol{A}d\boldsymbol{X})
\]
对于向量变元的标量函数：
\[
df(\mathbf{x})=\text{tr}(\mathbf{A}d\mathbf{x}) \text{ 等价于 } D_\mathbf{x}f(\mathbf{x})=\frac{\partial f(\mathbf{x})}{\partial\mathbf{x}^T}=\mathbf{A}
\]
对于矩阵变元的标量函数：
\[
df(\boldsymbol{X})=\text{tr}(\boldsymbol{A}d\boldsymbol{X}) \text{ 等价于 } D_\mathbf{x}f(\boldsymbol{X})=\frac{\partial f(\boldsymbol{X})}{\partial\boldsymbol{X}^T}=\boldsymbol{A}
\]
行偏导与梯度的关系：
\[
D_{\mathbf{x}}f(\boldsymbol{X})=\frac{\partial f(\boldsymbol{X})}{\partial\boldsymbol{X}^T}=\boldsymbol{A} \text{ 等价于 } \nabla_{\mathbf{x}}f(\boldsymbol{X})=\boldsymbol{A}^T
\]
\(f(x) = x^T A x\)
\[
f(x) = x^T A x
\]
求解
\[
\begin{aligned}
df(x) &= (dx^T) A x + x^T d(A x)\\
&= x^T A^T dx + x^T A dx\\
&= Tr(x^T (A^T + A) dx)
\end{aligned}
\]
\[
\begin{aligned}
D_x f(x) &= x^T (A^T + A) \\
\nabla_x f(x) &= D_x^T f(x) = (A^T + A) x \\
\text{if } A^T &= A \text{ then } \nabla_x f(x) = 2 A x
\end{aligned}
\]
\(f(X) = tr(A X^{-1})\)
\[
f(X) = tr(A X^{-1})
\]
\[
\begin{aligned}
d f(x)&=d\ \text{tr}(A^{-1}X)\\
&= \text{tr}\left[d(A^{-1}X)\right]\\
&= \text{tr}\left[A^{-1}dX\right]\\
&= \text{tr}\left[A^{-1}(-X^{-1}dX X^{-1})\right]\\
&= \text{tr}\left[-X^{-1}A^{-1}dX X^{-1}\right]\\
\end{aligned}
\]
最后一步运用了迹的性质
\[
tr(ABC) = tr(BCA) = tr(CAB)
\]
\[
D_Xf(X)=-X^{-1}A^{-1}X^{-1}
\]
复向量 ¶
复变量的偏导数定义：
\[
\begin{cases}
\frac{\partial}{\partial z}=\frac{1}{2}\left(\frac{\partial}{\partial x}-j\frac{\partial}{\partial y}\right)\\
\frac{\partial}{\partial z^*}=\frac{1}{2}\left(\frac{\partial}{\partial x}+j\frac{\partial}{\partial y}\right)
\end{cases}
\]
其中 x 和 y 是相互独立的 :
\[
\begin{cases}
\frac{\partial y}{\partial x}=0\\
\frac{\partial x}{\partial y}=0
\end{cases}
\]
可以证明 z 和 z* 也是相互独立的 :
\[
\begin{aligned}
\frac{\partial z}{\partial z^*}&=\frac{\partial x}{\partial z^*}+j\frac{\partial y}{\partial z^*}\\
&=\frac{1}{2}\left(\frac{\partial x}{\partial x}+j\frac{\partial x}{\partial y}\right)+j\frac{1}{2}\left(\frac{\partial y}{\partial x}+j\frac{\partial y}{\partial y}\right)\\
&=\frac{1}{2}(1+0)+j\frac{1}{2}(0+j)=0
\end{aligned}
\]
\[
\begin{aligned}
\frac{\partial z^*}{\partial z}&=\frac{\partial x}{\partial z}-j\frac{\partial y}{\partial z}\\
&=\frac{1}{2}\left(\frac{\partial x}{\partial x}-j\frac{\partial x}{\partial y}\right)-j\frac{1}{2}\left(\frac{\partial y}{\partial x}-j\frac{\partial y}{\partial y}\right)\\
&=\frac{1}{2}(1-0)-j\frac{1}{2}(0-j)=0
\end{aligned}
\]
对于单变量复函数，其梯度定义为：
\[
\nabla_zf(z,z^*)=\frac{\partial f(z,z^*)}{\partial z}|_{z^*=\text{常数}}
\]
共轭梯度
\[
\nabla_{z^*}f(z,z^*)=\left.\frac{\partial f(z,z^*)}{\partial z^*}\right|_{z=\text{常数}}
\]
其微分形式为：
\[
df(z,z^*)=\frac{\partial f(z,z^*)}{\partial z}dz+\frac{\partial f(z,z^*)}{\partial z^*}dz^*
\]
对于复变元向量：
\[
\mathbf{z}=\begin{bmatrix}z_1,z_2,\ldots,z_m\end{bmatrix}^T
\]
其微分形式可以写作：
\[
\begin{aligned}
df(\mathbf{z},\mathbf{z}^*)&=\left[\frac{\partial f(\mathbf{z},\mathbf{z}^*)}{\partial z_1},\cdots,\frac{\partial f(\mathbf{z},\mathbf{z}^*)}{\partial z_m}\right]\begin{bmatrix}dz_1\\\vdots\\dz_m\end{bmatrix}+\left[\frac{\partial f(\mathbf{z},\mathbf{z}^*)}{\partial z_1^*},\cdots,\frac{\partial f(\mathbf{z},\mathbf{z}^*)}{\partial z_m^*}\right]\begin{bmatrix}dz_1^*\\\vdots\\dz_m^*\end{bmatrix}\\
&=\frac{\partial f(\mathbf{z},\mathbf{z}^*)}{\partial\mathbf{z}^T}d\mathbf{z}+\frac{\partial f(\mathbf{z},\mathbf{z}^*)}{\partial\mathbf{z}^H}d\mathbf{z}^*
\end{aligned}
\]
对于复变量来说，通常要求两个梯度，一个是 \(\frac{\partial}{\partial z}\)，一个是 \(\frac{\partial}{\partial z^{*}}\)
Hession 矩阵 ¶
先求行偏导，再求梯度
实值函数 \(f(\mathbf{x})\) 相对于 \(m \times 1\) 实向量 \(\mathbf{x}\) 的二阶偏导称为 Hessian 矩阵，记作 \(\mathbf{H}[f(\mathbf{x})]\)，定义为
\[
\mathbf{H}[f(\mathbf{x})] = \frac{\partial^2 f(\mathbf{x})}{\partial \mathbf{x} \partial \mathbf{x}^T} = \frac{\partial}{\partial \mathbf{x}} \left[ \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}^T} \right] \in \mathbb{R}^{m \times m}
\]
或记作
\[
\mathbf{H}[f(\mathbf{x})] = \nabla_x^2 f(\mathbf{x}) = \nabla_x (D_x f(\mathbf{x}))
\]
或写作
\[
\mathbf{H(f)} = \nabla^{2} f(x)=\left[\begin{array}{cccc}
\frac{\partial^{2} f(x)}{\partial x_{1}^{2}} & \frac{\partial^{2} f(x)}{\partial x_{1} \partial x_{2}} & \ldots & \frac{\partial^{2} f(x)}{\partial x_{1} \partial x_{m}} \\
\frac{\partial^{2} f(x)}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f(x)}{\partial x_{2}^{2}} & \ldots & \frac{\partial^{2} f(x)}{\partial x_{2} \partial x_{m}} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^{2} f(x)}{\partial x_{m} \partial x_{1}} & \frac{\partial^{2} f(x)}{\partial x_{m} \partial x_{2}} & \ldots & \frac{\partial^{2} f(x)}{\partial x_{m}^{2}}
\end{array}\right]\in \mathbb{R}^{m \times m}
\]
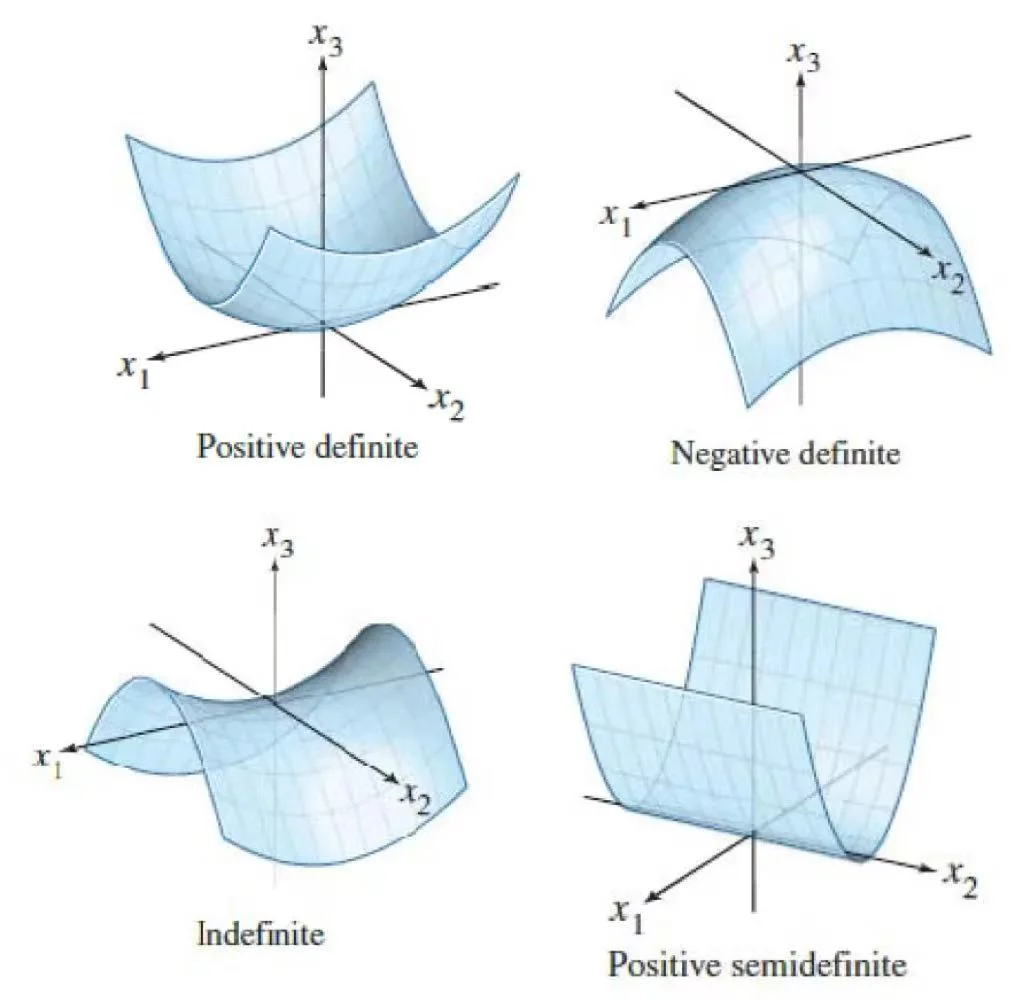
二次型理论
- \(\mathbf{H(f)}\) 负定，有极大值： 奇数阶主子式为负数，偶数阶为正数
- \(\mathbf{H(f)}\) 正定，有极小值：顺序主子式都为正数
- \(\mathbf{H(f)}\) 不定，鞍点：特征值有正有负
- \(\mathbf{H(f)}\) 不可逆，无法判断：特征值有 0
积分 ¶
\[
\int\mathbf{A}\mathrm{d}t=\begin{bmatrix}\int a_{11}\mathrm{d}t&\int a_{12}\mathrm{d}t&\cdots&\int a_{1n}\mathrm{d}t\\\int a_{21}\mathrm{d}t&\int a_{22}\mathrm{d}t&\cdots&\int a_{2n}\mathrm{d}t\\\vdots&\vdots&\ddots&\vdots\\\int a_{m1}\mathrm{d}t&\int a_{m2}\mathrm{d}t&\cdots&\int a_{mn}\mathrm{d}t\end{bmatrix}
\]