数据结构与算法 ¶

主定理 ¶

时间复杂度定义¶

定义 2.1: 如果存在正常数 \(c\) 和 \(m_{0}\) 使得当 \(N \geqslant m_{0}\) 时 \(T(N) \leqslant c f(N)\), 则记为 \(T(N)=O f(N)\) 。

定义 2.2: 如果存在正常数 \(c\) 和 \(m_{0}\) 使得当 \(N \geqslant m_{0}\) 时 \(T(N) \geqslant c g(N)\), 则记为 \(T(N)=\Omega(g(N))\) 。

** 定义 2.3: ** \(T(N)=\Theta(h(N))\) 当且仅当 \(T(N)=O(h(N))\) 且 \(T(N)=\Omega(h(N))\) 。

定义 2.4: 如果对每一正常数 \(c\) 存在常数 \(m_{0}\) 使得当 \(N \geqslant m_{0}\) 时 \(T(N) \leqslant c p(N)\), 则 \(T(N)=\) \(o(p(N))\) 。也可简述为, 如果 \(T(N)=O(p(N))\) 且 \(T(N) \neq \Theta(p(N))\), 则 \(T(N)=o(p(N))\) 。

定义 2.5： 若存在 c>0 和 n0，当 N>n0 时，T(N)>cq(N)，则记为 T(N) = w(q(N))

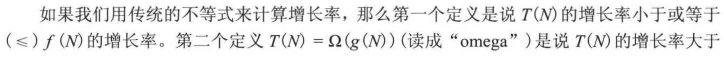
\(O(1)\) 是指 \(f(n)\) 有上界

法则 1,2,3¶

主要考虑 最坏可能性 与 平均可能性

等价关系 ¶

find: 返回包含给定元素的集合

union: 把含有两个等价类合并成一个新的等价类

采用森林 每个节点都只有父节点信息代表类 合并操作只要修改父节点信息即可

合并时采用高度或者大小合并 不要太偏向于一边