注意力机制 ¶
约 4444 个字 10 张图片 预计阅读时间 17 分钟
个人学习流程:
3b1b 视频 ➡️ 李宏毅视频 ➡️ 李沐视频 ➡️ 论文阅读 ➡️ 代码实战 ➡️ 公司面试八股
- 各个层的参数数量整理
- 时间复杂度计算
对比 ¶
对应 paper 中 abstract、background
vs CNN¶
CNN 只考虑卷积核的感受野,而 attention 考虑整个序列
所以卷积难以考虑较长的序列,如果距离较远的话,需要很多层卷积才可以达到效果;
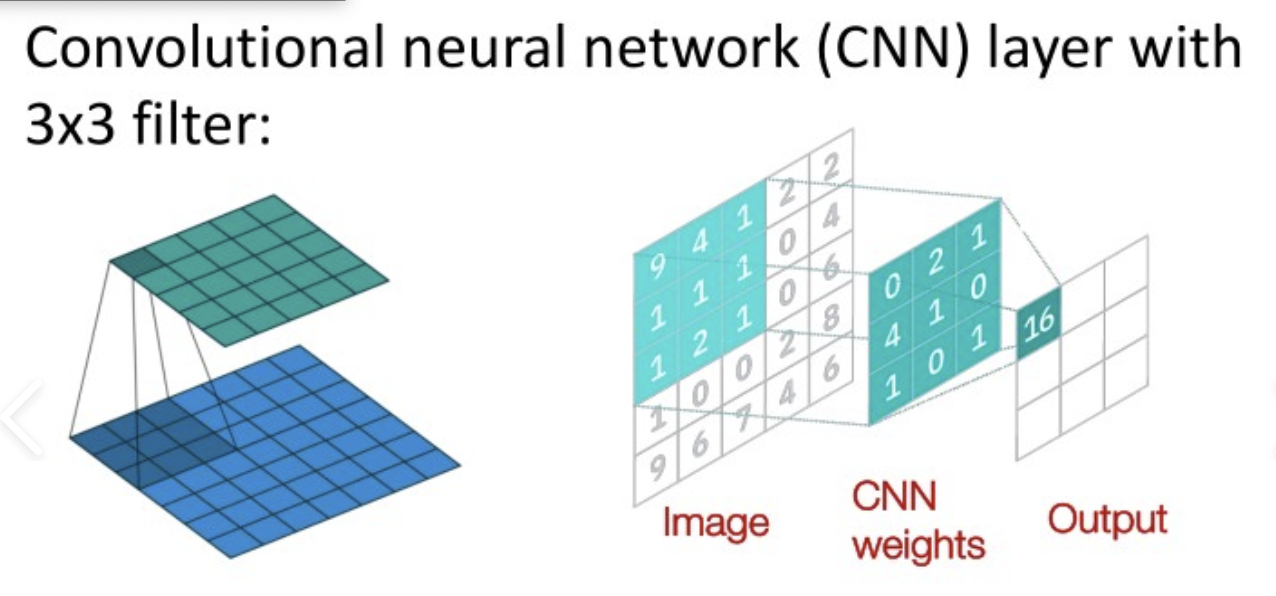
图源网络,侵删
而 attention 可以考虑整个序列,所以可以考虑较长的序列
可以说 CNN 是 attention 的特例
attention 也可以说是特殊的 CNN,相当于 CNN 的 receptive filed 是 learn 出来的
graph TD
subgraph Self-Attention["Self-Attention"]
style Self-Attention fill:#e6f3ff,stroke:#2196f3,stroke-width:4px,rx:50,ry:50
D[Learnable Global<br/>Receptive Field]
subgraph CNN["CNN"]
style CNN fill:#ffe6e6,stroke:#f44336,stroke-width:2px,rx:30,ry:30
C[Fixed Local<br/>Receptive Field]
end
end
style D fill:none,stroke:none
style C fill:none,stroke:none- data 较少的时候,CNN 训练效果好
- 数据量较大的时候,attention 效果好,有 scaling 效应
vs RNN¶
- RNN 计算 \(h_t\) 的时候,需要考虑 hidden state \(h_{t-1}\) and the input for position \(t\)
- 很早期的信息在后续计算的时候可能会丢失,做大的 ht 对内存开销较大
- RNN 虽然可以双向,但是不可以并行计算,对 memory 要求高
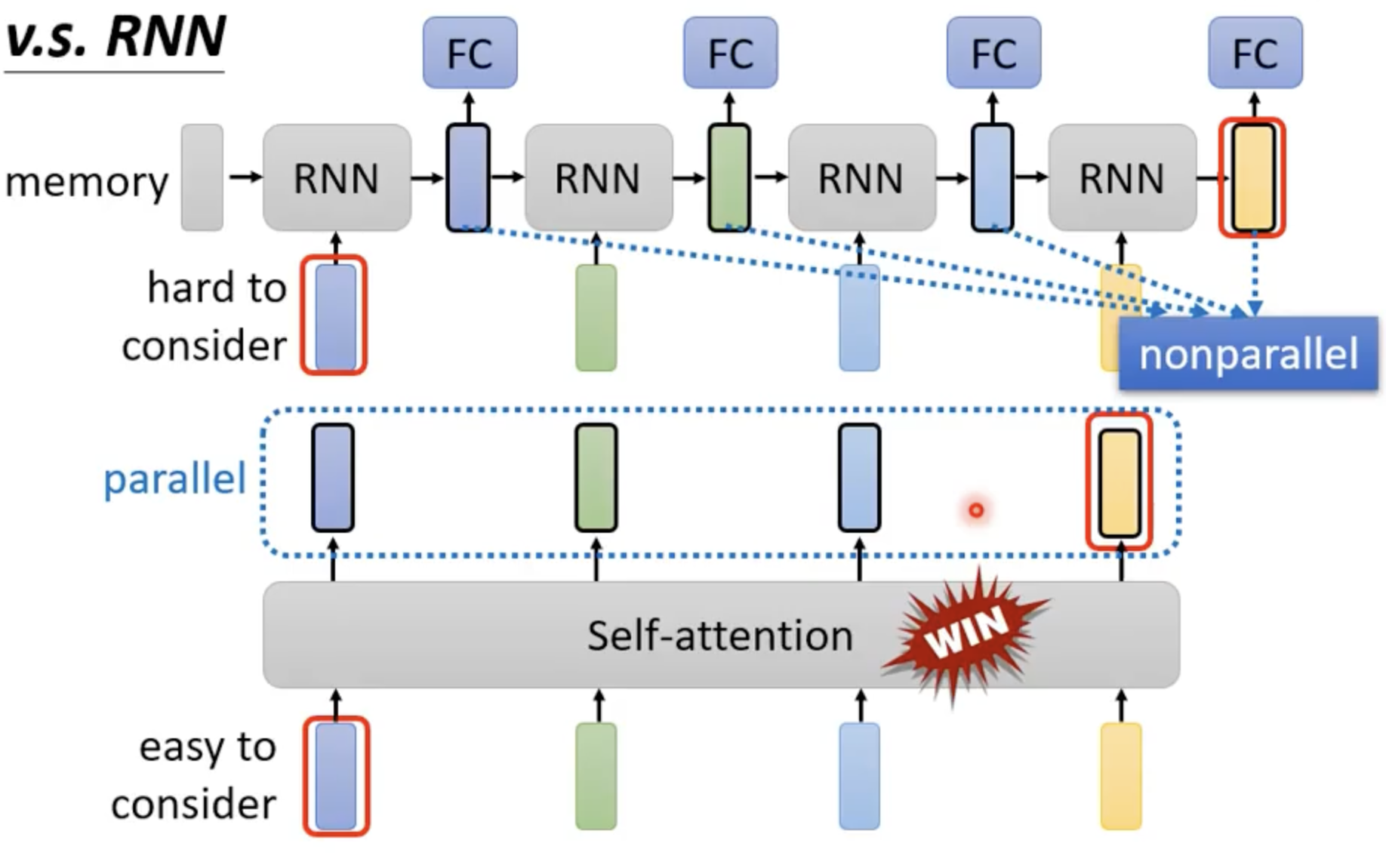
vs GNN¶
- 应用在 gragh 结构上的时候,可以使用 edge 已经给出的连接关系,直接计算 attention score,其他节点可以直接设置成 0
graph LR
subgraph Graph["Node Graph"]
1((1)) --- 8((8))
1 --- 6((6))
1 --- 7((7))
6 --- 7
6 --- 5((5))
5 --- 4((4))
5 --- 3((3))
3 --- 2((2))
end
subgraph Matrix["Attention Matrix"]
M["1 2 3 4 5 6 7 8<br/>□ □ □ □ ■ ■ □ ■<br/>□ □ ■ □ □ □ □ □<br/>□ ■ □ □ □ □ □ □<br/>□ □ □ □ ■ □ □ □<br/>■ □ □ ■ □ □ □ □<br/>■ □ □ □ □ □ □ □<br/>□ □ ■ □ □ □ □ □<br/>■ □ □ □ □ □ □ □"]
end
style 1 fill:#000000,stroke:#000000,color:#fff
style 2 fill:#000000,stroke:#000000,color:#fff
style 3 fill:#000000,stroke:#000000,color:#fff
style 4 fill:#000000,stroke:#000000,color:#fff
style 5 fill:#000000,stroke:#000000,color:#fff
style 6 fill:#000000,stroke:#000000,color:#fff
style 7 fill:#000000,stroke:#000000,color:#fff
style 8 fill:#000000,stroke:#000000,color:#fff
style M fill:none,stroke:noneSelf-Attention¶
思考下面的问题:
- 同一个词汇,放在句子不同位置,它的语义可能不同(我们需要上下文信息
) :可以开 window 解决 - 但如果输入是一个变长的序列:开 window 就解决不了了
所以需要一个机制,让每个词汇都考虑整个序列的信息(这个序列是变长的
word embedding¶
word2vec:获得词汇的最初始含义
Word embedding.
- 嵌入是一个“抽象”的过程,把高维向量嵌入到一个低维度当中
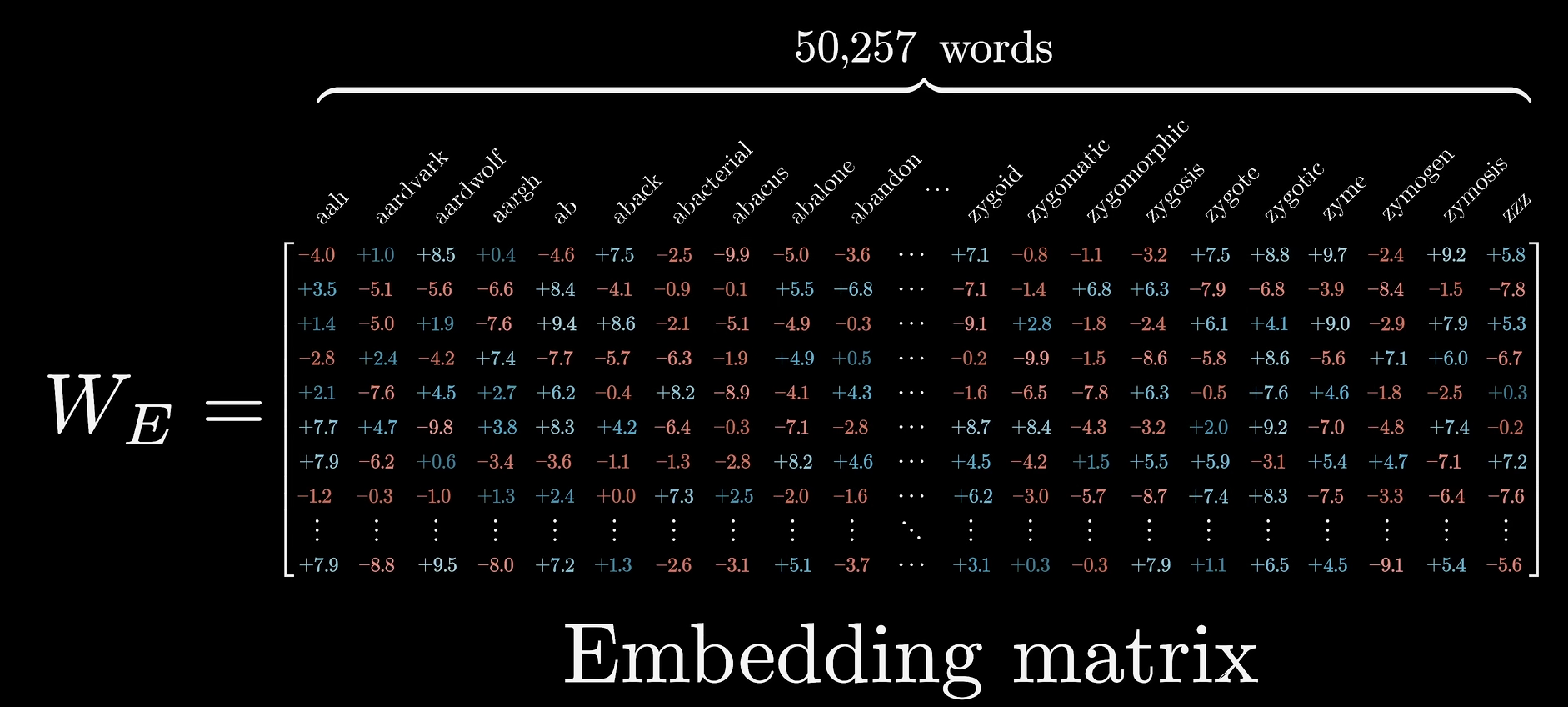
in the embedding layers, we multiply weights by \(\sqrt{d_{model}} = \sqrt{512}\) 防止,维度一高,导致初始时候与position encoding的值相差太大
position encoding¶
我们不仅仅需要考虑词汇的语义信息,还需要考虑词汇的位置信息,所以需要一个 position encoding
位置编码通过向每个位置的词嵌入添加一个特定的向量来实现,其中第 \(i\) 个位置的第 \(2k\) 或 \(2k+1\) 维的位置编码分别为:
- \(pos\) 是序列中的位置(从 0 开始)
- \(i\) 是维度索引(从 0 开始)
- \(d_{model}\) 是词嵌入的维度
这种正弦和余弦函数的使用使得模型能够区分不同位置的词,并使得模型能够学习到位置的相对关系,解决了 Transformer 模型自身不具备处理序列中元素顺序信息的问题。
当然表示位置的算法可以自己创造 可学习的位置编码、相对位置编码、旋转位置编码(RoPE)
Attention 计算 – scaled dot-product attention¶
word embedding 解决了词汇本身的含义,position encoding 附加了词汇的位置信息,那么词汇的不同位置(或者说上下文信息)是如何影响到这个词汇的最终含义呢?
这里涉及到计算 attention score,如何计算 attention score 呢?
我们使用三个矩阵,来计算 attention score
- \(Q\): query
- \(K\): key
- \(V\): value, 如何让前面的词汇影响后面的词汇,word embedding 乘上这个矩阵得到一个转移到向量
attention 分数:\(K\) 与 \(Q\) 的点积,可以看作 \(K\) 与 \(Q\) 的相似度,为 value 矩阵提供权重。对于如果 \(Q\) 和 \(K\) 相似度很高,那么就给予 \(V\) 更多的权重
\(d_k\) 是 Q 和 K 的维度,因为 Q 和 K 的维度是相同的,在论文中是 \(d_k = 512\)
如果 \(d_k\) 很大,那么 \(QK^T\) 的值会很大,导致 softmax 的值趋近于 1,导致梯度消失 所以需要除以\(\sqrt{d_k}\) 来归一化
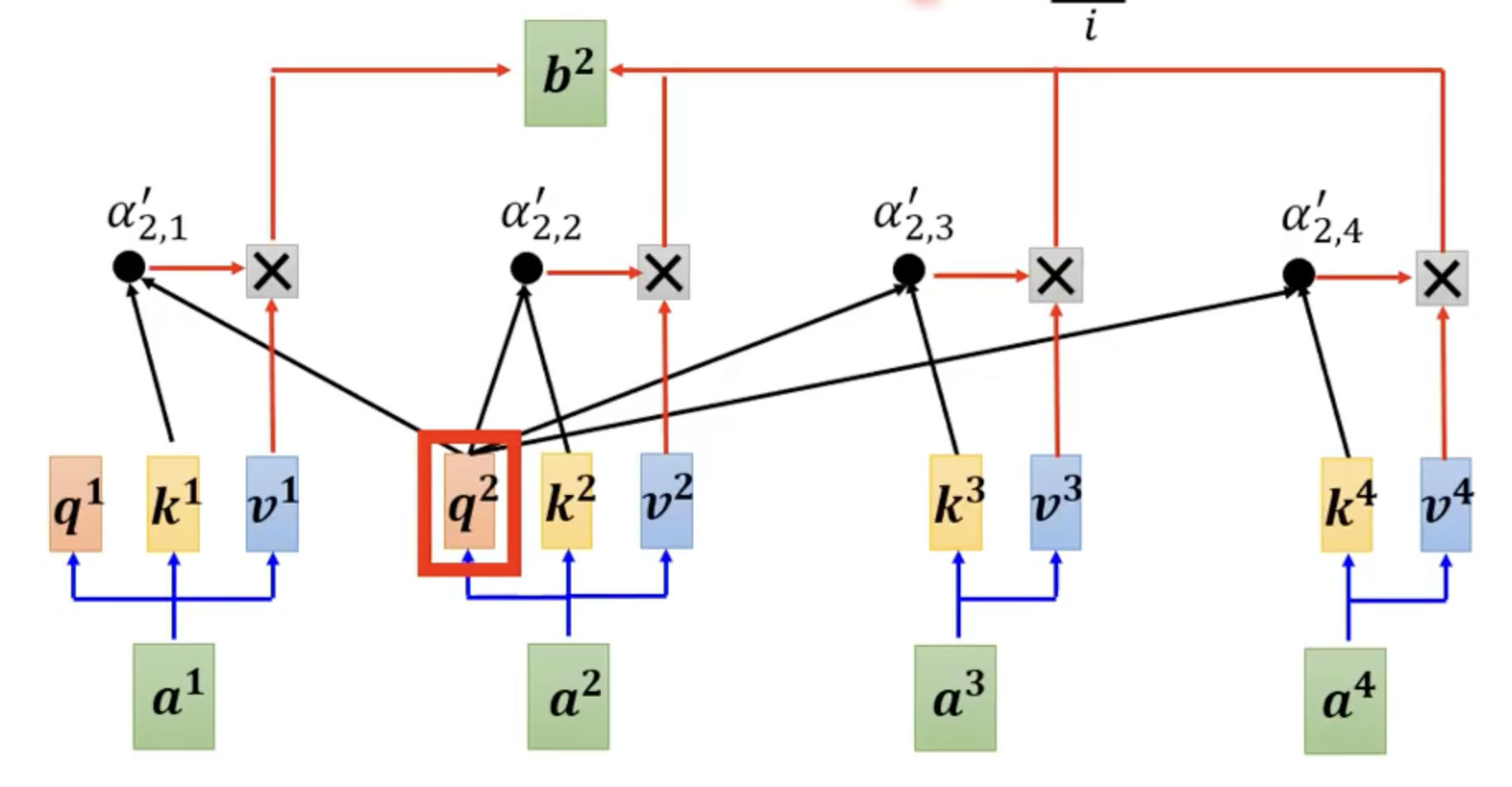
图片来源:李宏毅老师 ppt

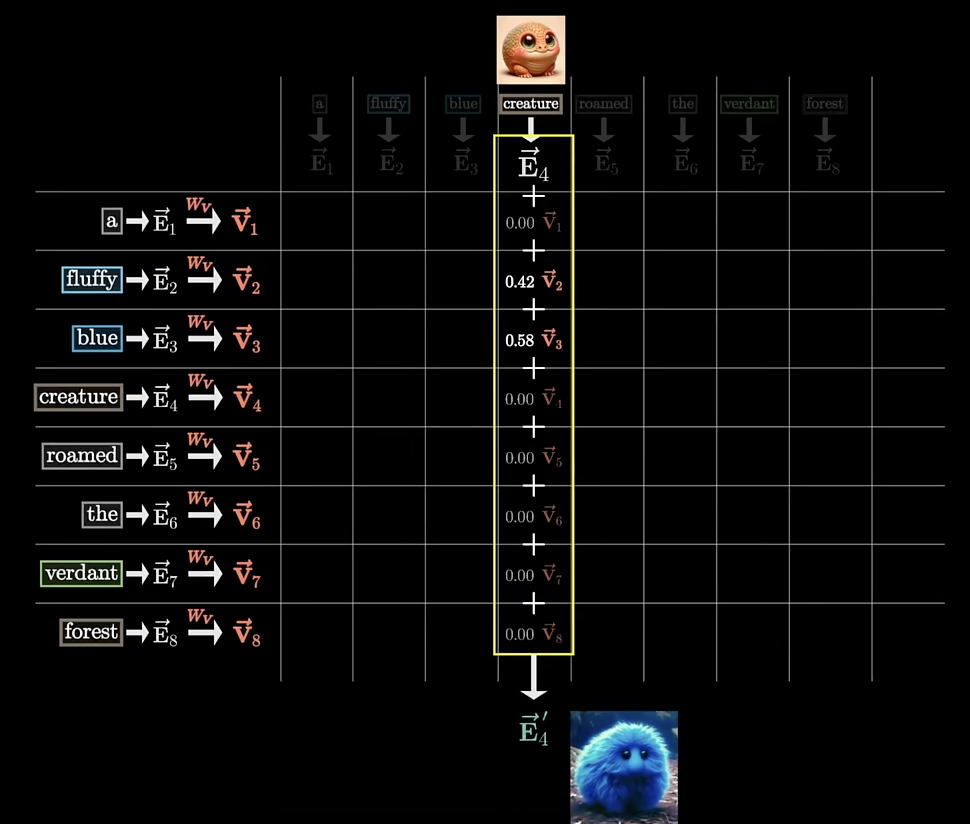
图片来源:3b1b
点积能够有效衡量两个向量的相似性。在注意力机制中,通过计算查询向量(Query)和键向量(Key)的点积,可以评估它们之间的相关性,从而决定注意力权重
attention 的注意力矩阵的计算为什么用乘法而不是加法?
为了计算更快。
注意力机制有两种
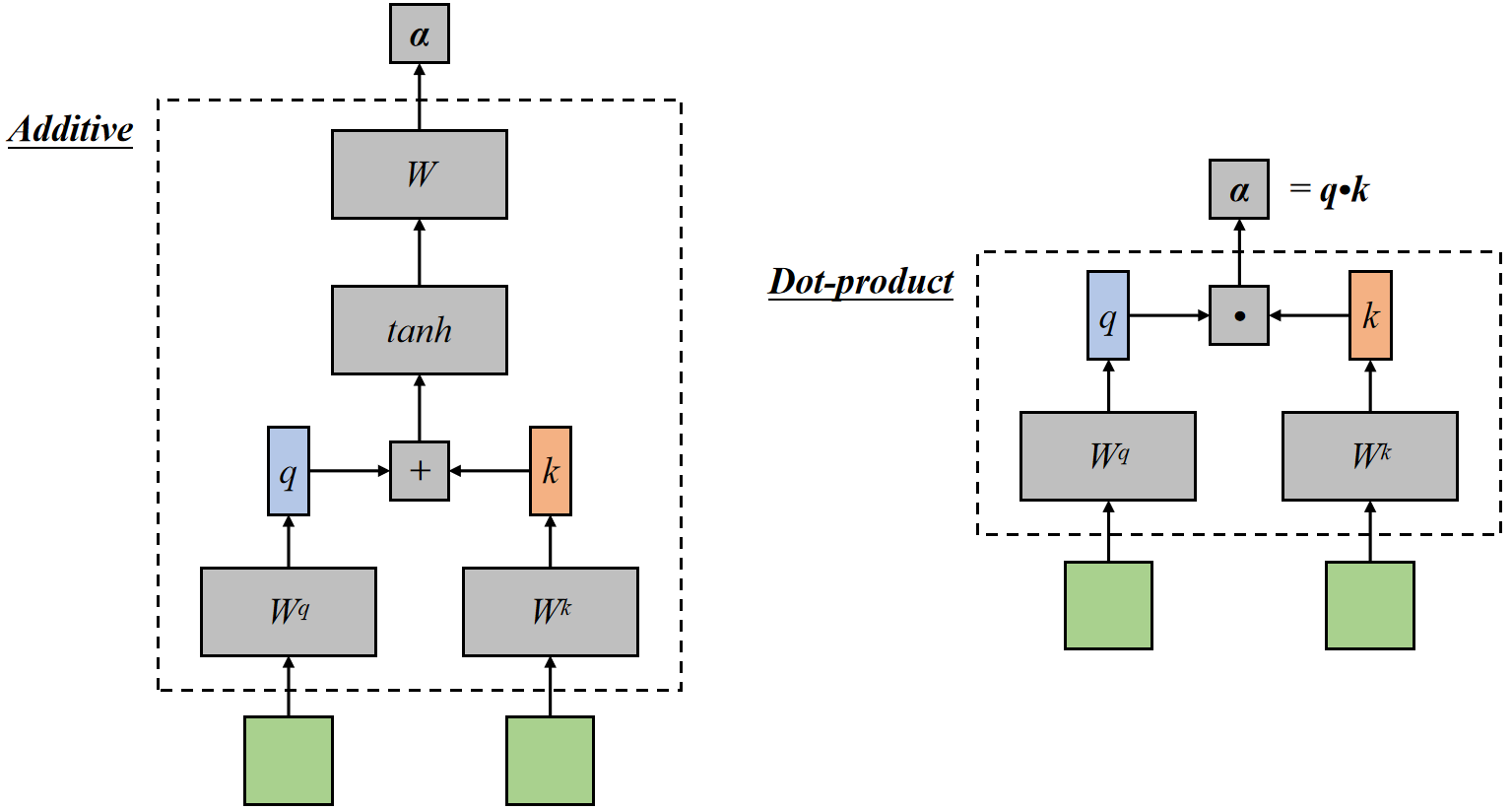
加法形式是先加、后 tanh、再和 V 矩阵相乘,相当于一个完整的隐层。
计算复杂度
- 在计算复杂度上,乘法和加法理论上的复杂度相似,但是在实践中,乘法可以利用高度优化的矩阵乘法代码 ( 有成熟的加速实现 ) 使得点乘速度更快,空间利用率更高。( 论文 P4 有解释 )
- 加性注意力需要额外的全连接层和非线性变换,计算复杂度高,且不好并行
- 点积可通过除以根号下 dk 进行缩放缓解梯度问题,加性注意力的不如其稳定;在 \(d_k\) 较小的时候,加法和乘法形式效果相近。但是随着 \(d_k\) 增大,加法开始显著优于乘法。作者认为,\(d_k\) 增大导致乘法性能不佳的原因,是极大的点乘值将整个 softmax 推向梯度平缓区,使得收敛困难。于是选择 scale,除 \(\sqrt{d_k}\)。
为什么 \(Q、K、V\) 相同
自注意力机制中,\(Q、K、V\) 都是从同一个输入序列 \(x\) 中生成的,是因为:
自注意力 的目标是捕捉输入序列中元素之间的依赖关系,因此需要让每个元素同时作为 Query、Key 和 Value
通过这种方式,模型可以计算每个元素与其他元素之间的关系,并生成上下文相关的表示
Transformer 中为什么需要线性变换?
输入:\(x\) 维度为 \([batch\_size, seq\_length, embed\_dim]\)
线性投影:将输入 \(x\),分别乘以 \(w_q, w_k, w_v\),生成 \(Q、K、V\) - \(w\)的维度都是 \([batch\_size, embed\_dim, embed\_dim]\) - \(Q, K, V\)的维度都是 \([batch\_size, seq\_length, embed\_dim]\)
\(K\)、\(Q\)、\(V\) 分别是输入向量经过不同的线性变换矩阵 \(W_k\)、\(Q_k\)、\(V_k\) 计算得到。可以从正反两面分析线性变换的必要性:
线性变换的好处:在 \(QK^T\) 部分,线性变换矩阵将 KQ 投影到了不同的空间,增加了表达能力 ( 这一原理可以同理 SVM 中的核函数 - 将向量映射到高维空间以解决非线性问题),这样计算得到的注意力矩阵的泛化能力更高。
不用线性变换的坏处:在 \(QK^T\) 部分,如果不做线性变换,即 X=Q=K, 则会导致注意力矩阵是对称的,即 \(d(x_1,x_2)=d(x_2,x_1)\), 这样的效果明显是差的,比如“我是一个女孩”这句话,女孩对修饰我的重要性应该要高于我修饰女孩的重要性。
预测时候,把最后一个词乘上一个矩阵,得到映射到词库上面的得分,经过 softmax 层后,就有了概率分布
softmax:指数放缩后再归一化
我们需要归一化的系数,来作为计算语意移动操作的权重
同时让高值更多权重,采样的时候,让高值更容易被采样到
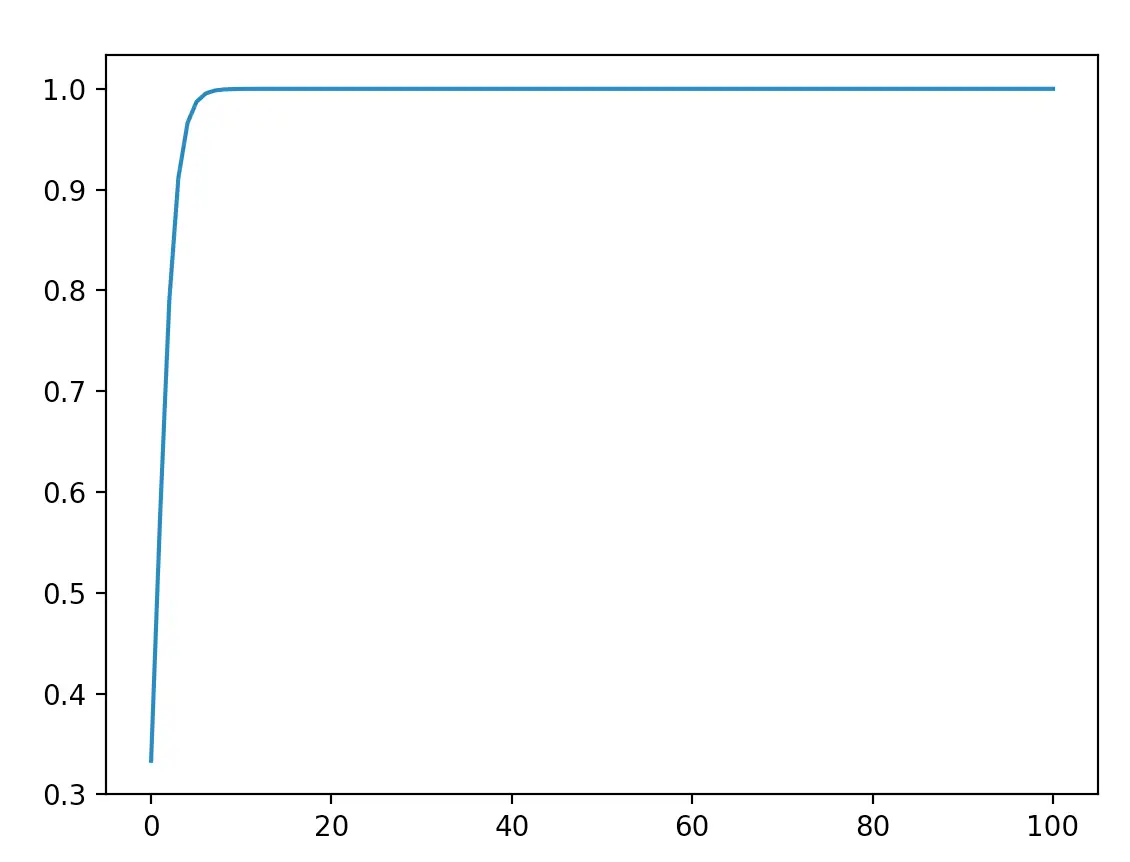
在数量级较大时,softmax 将几乎全部的概率分布都分配给了最大值对应的标签。
这里要引入一个超参数 T,来控制 softmax 的放缩。可以类比化学反应中的温度。T 越大,活性越小,softmax 的放缩越大,即让高值更多权重。
T 较大的时候,让放缩较小,即让低值更多权重
Transformer attention 计算为什么要在 softmax 这一步之前除以 \(\sqrt{d_k}\)
Nil-9 - transformer 中的 attention 为什么 scaled? - 知乎
- 取决于 Softmax 的性质,如果 softmax 内计算的数过大或者过小,可能导致 Softmax 后的结果为 0,导致梯度消失
- 为什么是 \(d_k\)。假设 \(Q\)、\(K\) 中元素的值分布在 \([0,1]\), softmax 的计算中,分母涉及了一次对所有位置的求和,整体的分布就会扩大到 \([0,d_k]\)。
\(d_k\) 是 \(Q\) 和 \(K\) 的维度,因为 \(Q\) 和 \(K\) 的维度是相同的,在论文中是 \(d_k = 512\)
softmax 的梯度推导
给定输入 \(\mathbf{x} = [x_1, x_2, \dots, x_n]\),softmax 输出为:
分两种情况讨论:
综上
其中 \(\delta_{ij}\) 是 Kronecker delta:\(\delta_{ij} = \begin{cases} 1 & \text{if } i = j \\ 0 & \text{if } i \ne j \end{cases}\)
写成矩阵形式(Jacobian
记 softmax 输出为 \(\mathbf{\hat{y}} = [\hat{y}_1, \dots, \hat{y}_n]^\top\),则:
- \(\text{diag}(\mathbf{\hat{y}})\) 是对角矩阵,对角线为 \(\hat{y}_i\)
- \(\mathbf{\hat{y}} \mathbf{\hat{y}}^\top\) 是外积,得到一个 rank-1 矩阵
梯度消失的推导
然后我们来看 softmax 的梯度。不妨简记 softmax 函数为 \(g(\cdot)\),softmax 得到的分布向量 \(\hat{\mathbf{y}} = g(\mathbf{x})\) 对输入 \(\mathbf{x}\) 的梯度为:
把这个矩阵展开:
根据前面的讨论,当输入 \(\mathbf{x}\) 的元素均较大时,softmax 会把大部分概率分布分配给最大的元素,假设我们的输入数量级很大,最大的元素是 \(x_1\),那么就将产生一个接近 one-hot 的向量 \(\hat{\mathbf{y}} \approx [1, 0, \cdots, 0]^{\top}\),此时上面的矩阵变为如下形式:
也就是说,在输入的数量级很大时,梯度消失为 0,造成参数更新困难。
维度与点积大小的关系
假设向量 \(q\) 和 \(k\) 的各个分量是互相独立的随机变量,均值是 0,方差是 1,那么点积 \(q \cdot k\) 的均值是 0,方差是 \(d_k\)
对 \(\forall i = 1, \cdots, d_k\),\(q_i\) 和 \(k_i\) 都是随机变量,
记 \(X = q_i\),\(Y = k_i\)
有:\(D(X) = D(Y) = 1\),\(E(X) = E(Y) = 0\)
则:
这样 \(\forall i = 1, \cdots, d_k\),\(q_i \cdot k_i\) 的均值是 0,方差是 1,又由期望和方差的性质,对相互独立的分量 \(Z_i\),有
所以有 \(q \cdot k\) 的均值 \(E(q \cdot k) = 0\),方差 \(D(q \cdot k) = d_k\) 。
方差越大也就说明,点积的数量级越大(以越大的概率取大值
将方差控制为 1,也就有效地控制了前面提到的梯度消失的问题。
为什么在分类层 ( 最后一层 ), 使用非 scaled 的 softmax?
同上面一部分,分类层的 softmax 也没有两个随机变量相乘的情况。此外,这一层的 softmax 通常和交叉熵联合求导,在某个目标类别 \(i\) 上的整体梯度变为 \(y_i^{\prime}-y_i\) , 即预测值和真值的差。
当出现某个极大的元素值,softmax 的输出概率会集中在该类别上。如果是预测正确,整体梯度接近于 0, 抑制参数更新;如果是错误类别,则整体梯度接近于 1,给出最大程度的负反馈。
也就是说,这个时候的梯度形式改变,不会出现极大值导致梯度消失的情况了。
交叉熵 + softmax 的梯度推导
- softmax 函数记为:
- 交叉熵损失函数定义为:
- 整体函数组合为:
根据链式法则:
即
写成矩阵形式
最后一个词向量,成为预测下一个词的 logit
Multi-Head Attention¶
- 捕捉更多样的特征
- 单头 只能从一个子空间计算注意力权重,可能无法充分捕捉输入序列中复杂的依赖关系
- 多头 通过将输入映射到多个子空间,每个头可以关注不同的特征或模式
- 增强模型的表达能力
- 提高泛化能力
- 并行计算 多头注意力机制可以并行计算多个注意力头,充分利用 GPU 的并行计算能力
多头注意力,模型能学习到根据上下文改变语意的多种方式。使用多个线性层投影到低维空间,再进行 attention 计算,那么线性层的 \(\omega\) 的参数是可以学习的。
使用不同的 \(Q\),学习不同种类的相关性
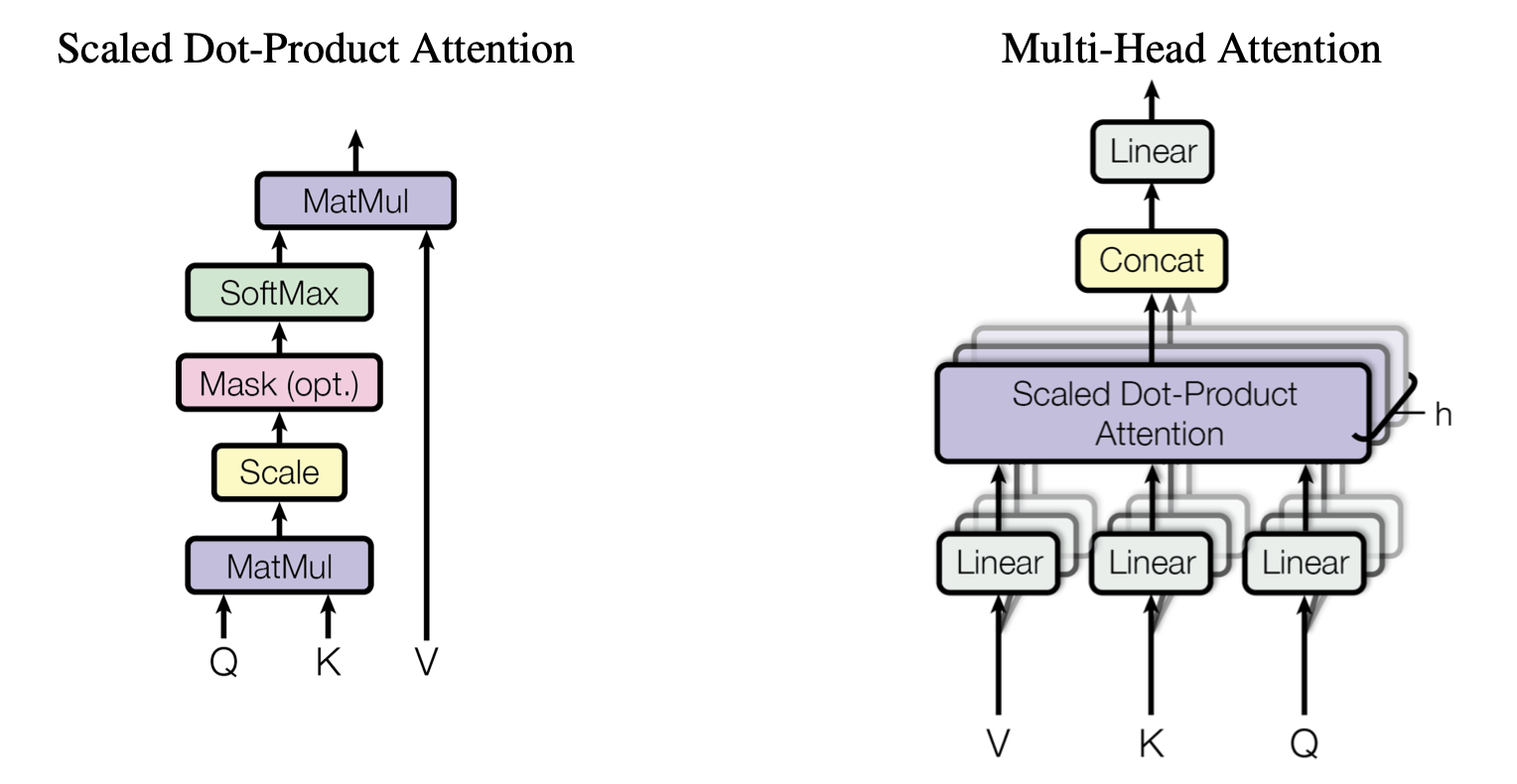
多头注意力机制首先将 Q、K、V 通过不同的线性变换映射到不同的表示空间,然后在每个表示空间上独立地应用自注意力机制,最后将所有头的输出拼接并再次线性变换得到最终输出。
在多头注意力机制中,原始维度 \(d_{model}\) 被拆分成 \(h\) 个较小的维度 \(d_k\),每个头对应的维度为 \(d_k\),使得每个头可以并行处理。
数学上,设有 \(h\) 个头,对于第 \(i\) 个头
最终输出为:
这种方式能够使模型在不同的子空间捕捉到序列的不同特征,从而提高性能。
改进 ¶
attention 对于模型的假设更少,所以需要更大的模型,更多的数据量,更多的计算时间,才能达到好的效果
Transformer 计算量最大的部分是哪里
多头注意力部分计算量最大。
假设完成一次推理,\(b=1\)(batch-size), \(s=256\)(seq-length, 序列最大长度 ), \(h=768\)(hidden-size), \(head=12\)(attention-head)
经过一个 Transformer 的多头注意力 block, 所需要的矩阵乘法的数量 : 1. \(Q[s, \frac{h}{12}] \times K[\frac{h}{12}, s] = Q[256, 64] \times K[64, 256]\) - 计算量: \(s^2 \times \frac{h}{12} = 256 \times 64 \times 256\) - 结果: \(Score[256, 256] = Score[s, s]\)
- \(Score[s, s] \times V[s, \frac{h}{12}] = Score[256, 256] \times V[256, 64]\)
- 计算量 : \(s^2 \times \frac{h}{12} = 256 \times 256 \times 64\)
总计算量 : \(12 \times (256 \times 64 \times 256 + 256 \times 256 \times 64) = 1\) 亿次乘法
除矩阵乘法外的其他运算 :
-
除以 \(\sqrt{d_k}\)
- 计算量 : \(s^2 = 256 \times 256\)
-
Softmax 函数
- 计算量 : \(s \times (s+s-1) \approx s^2\)
补充说明 :
-
两个矩阵相乘的计算量
- 矩阵 \(A\) 尺寸为 \((m,n)\)
- 矩阵 \(B\) 尺寸为 \((n,k)\)
- 计算量为 \(m \times n \times k\)
-
权重矩阵 \(K,Q,V\) 的尺寸
- 不考虑多头注意力 : 均为 \((s,h)\)
- 多头注意力 (12 头 ): 单头尺寸为 \((s,\frac{h}{12})\)
速度 & 准确 ¶
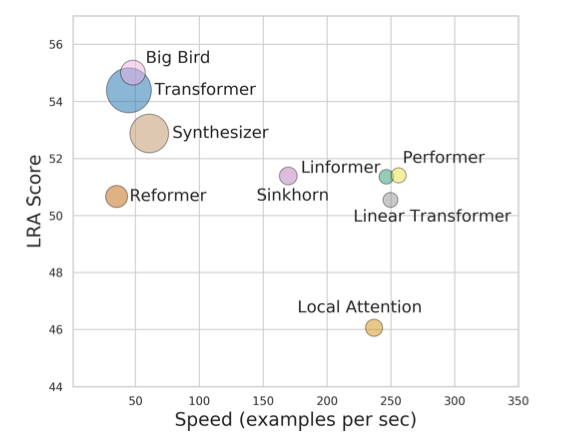
训练速度 ¶
attention is not all you need¶
Acknowledgement¶
- 王几行 XING - 大模型 -Transformer 面试八股文,简单背一背 - 知乎
- SweetBean - 算法岗常见面试题(八
) :Transformer_ 牛客网
- ch3nboyu - Transformer-interview: Transformer 面试常见八股