PID 控制 ¶

PID 控制是比例积分微分控制的简称，将偏差的比例 (P)、积分 (I) 和微分 (D) 通过线性组合构成控制量。

至今在全世界过程控制中用的 84% 仍是纯 PID 调节器，若改进型包含在内则超过 90%。

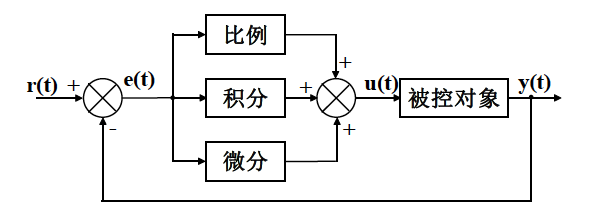
建模 ¶

连续系统 ¶

时域形式频域形式

\[ u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau) d\tau + K_d \dot{e}(t) \]

K 是比例，I 是一阶积分（滞后），D 是一阶微分（超前）

其中： - $ u(t) $ 是控制量。 - $ e(t) $ 是误差，即设定值与实际值之间的差。 - $ K_p $ 是比例增益。 - $ K_i $ 是积分增益。 - $ K_d $ 是微分增益。 - $ \Delta e(t) $ 是误差的变化量。 - $ \Delta t $ 是时间间隔。

可以测频率响应，进而使用补偿

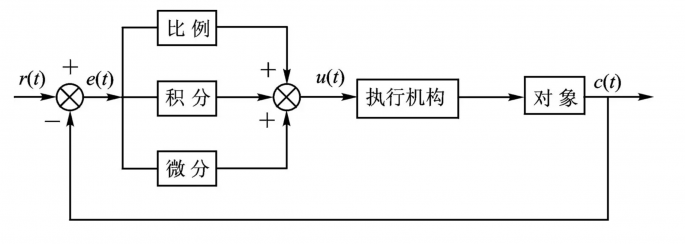
\[ G_c(s) = K_c \left( 1 + \frac{1}{\tau_I s} + \tau_D s \right) \]

离散 - 位置式 PID ¶

\[ u(k) = K_c \left\{ e(k) + \frac{T_s}{\tau_I} \sum_{j=0}^{k} e(j) + \frac{\tau_D}{T_s} [e(k) - e(k-1)] \right\} + u_0 \]

推导

推导：连续时间域的位置型公式：

\[ u(t) = K_c \left[ e(t) + \frac{1}{\tau_I} \int_0^t e(t) dt + \tau_D \frac{de(t)}{dt} \right] + u_0 \]

在离散时间中表示积分和微分可以使用下面的近似：

\[ \int_0^t e(\tau) d\tau \approx T_s \sum_{j=0}^{k} e(j),\quad \frac{de(t)}{dt} \approx \frac{e(k) - e(k-1)}{T_s} \]

得到离散时间域的位置型公式：

\[ u(k) = K_c \left\{ e(k) + \frac{T_s}{\tau_I} \sum_{j=0}^{k} e(j) + \frac{\tau_D}{T_s} [e(k) - e(k-1)] \right\} + u_0 \]

其中，$T_s$ 是采样时间，$u_0$ 是初始控制量。

离散 - 增量式 PID ¶

\[ \Delta u(k)=u(k)-u(k-1)=K_c\left\{[e(k)-e(k-1)+\frac{T_s}{\tau_I}e(k)+\frac{\tau_D}{T_s}[e(k)-2e(k-1)+e(k-2)]\right\} \]

\[ u(k)=u(k-1)+\Delta u(k) \]

给出的是执行机构在采样时刻 $k$ 时的增量值

对比 ¶

当然可以，以下是增量式和位置式 PID 控制的全面优缺点对比表：

特性	增量式 PID	位置式 PID
初始条件	不需要引入初始阀位值	需要引入初始阀位值
积分饱和	不会产生积分饱和	需要防积分饱和
输出条件	只有存在偏差时才会有输出	输出与整个过去的状态有关，用到了误差的累加值
手动到自动切换	容易实现从手动到自动的切换	可能存在较大冲击
累积误差	增量式 PID 控制的累积误差相对更小	位置式 PID 控制的累积误差相对更大
优点	1. 算式中不需要累加，控制增量 Δu(k) 的确定仅与最近 3 次的采样值有关，容易通过加权处理获得比较好的控制效果 2. 计算机每次只输出控制增量，即对应执行机构位置的变化量，故机器发生故障时影响范围小、不会严重影响生产过程 3. 手动—自动切换时冲击小，可以作到无扰动切换	1. 输出与整个过去的状态有关，可能更稳定 2. 易于理解和实现
缺点	1. 需要对控制量进行记忆 2. 存在稳态误差	1. 可能产生积分饱和 2. 累积误差较大

结构形式 ¶

并联式：$G_c(s)=K_c(1+\frac{1}{\tau_Is}+\tau_Ds)$

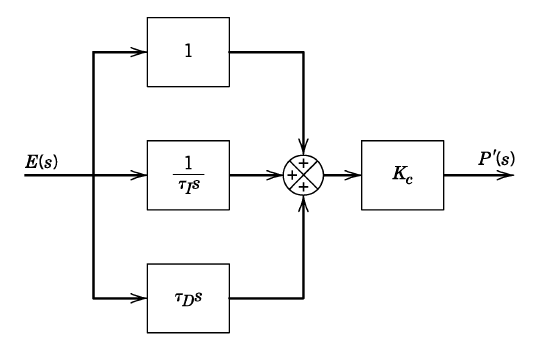
串联式：$G_c(s)=K_c(1+\frac{1}{\tau_Is})(1+\tau_Ds)$

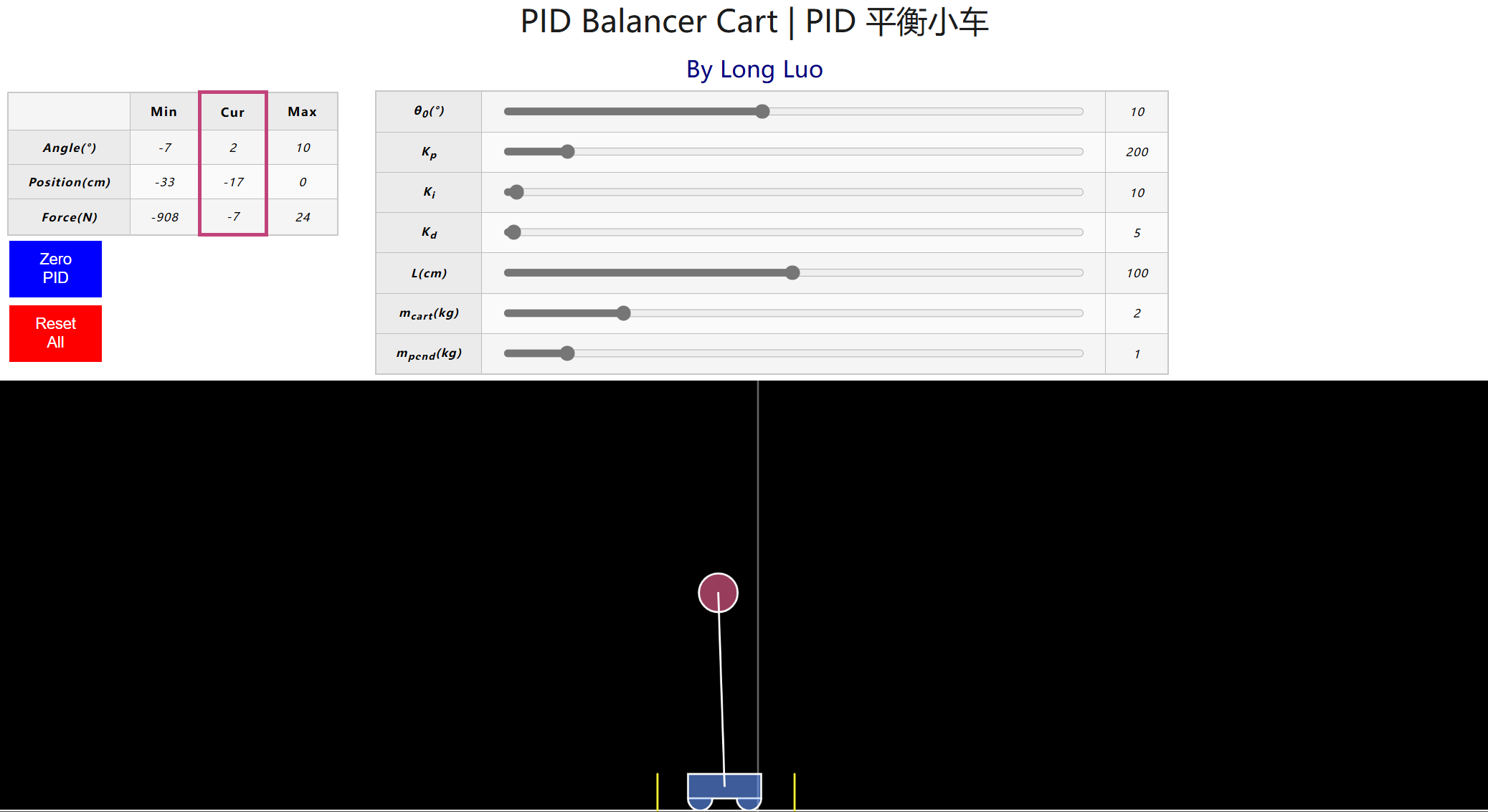
可视化 ¶

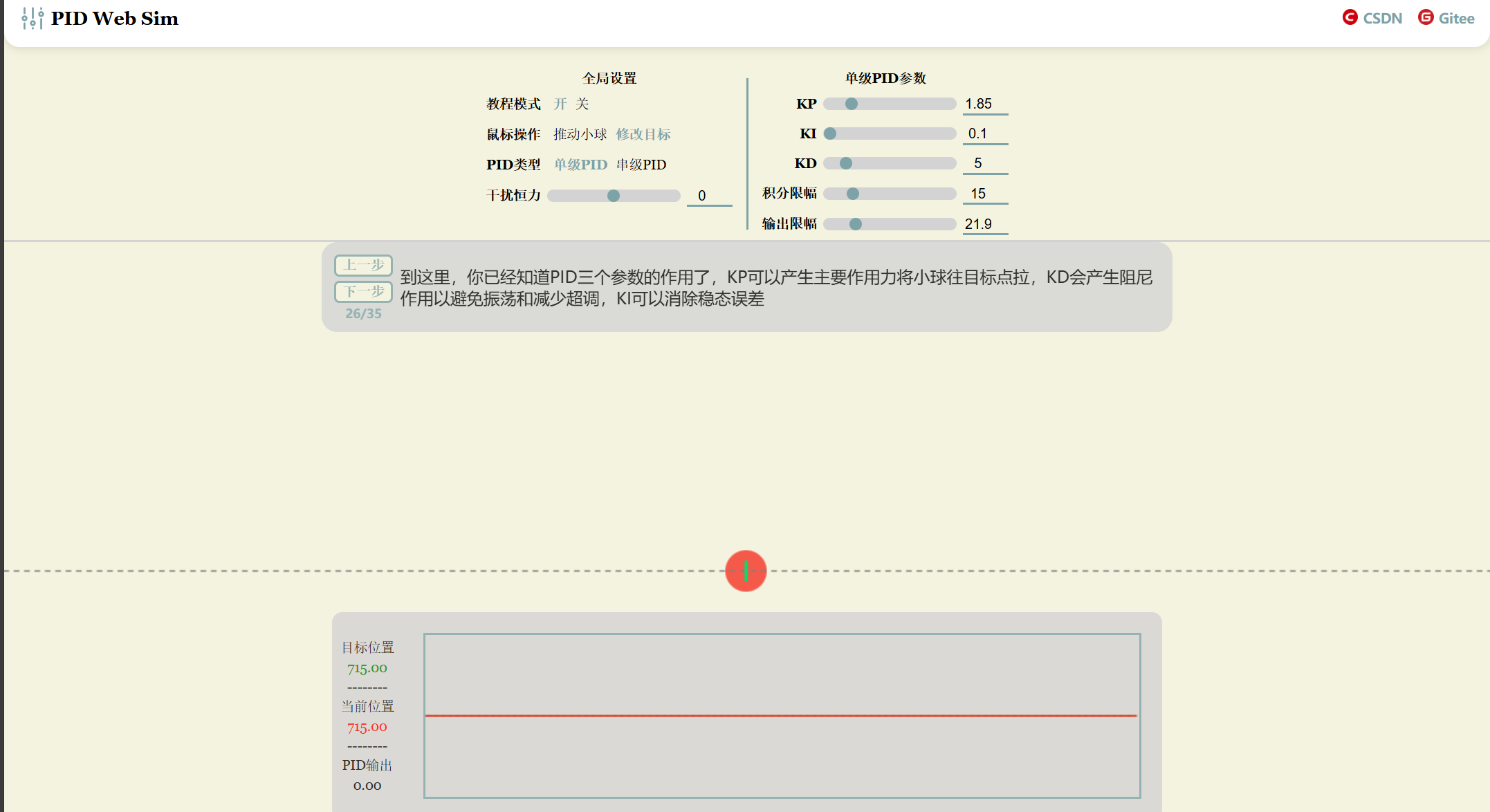
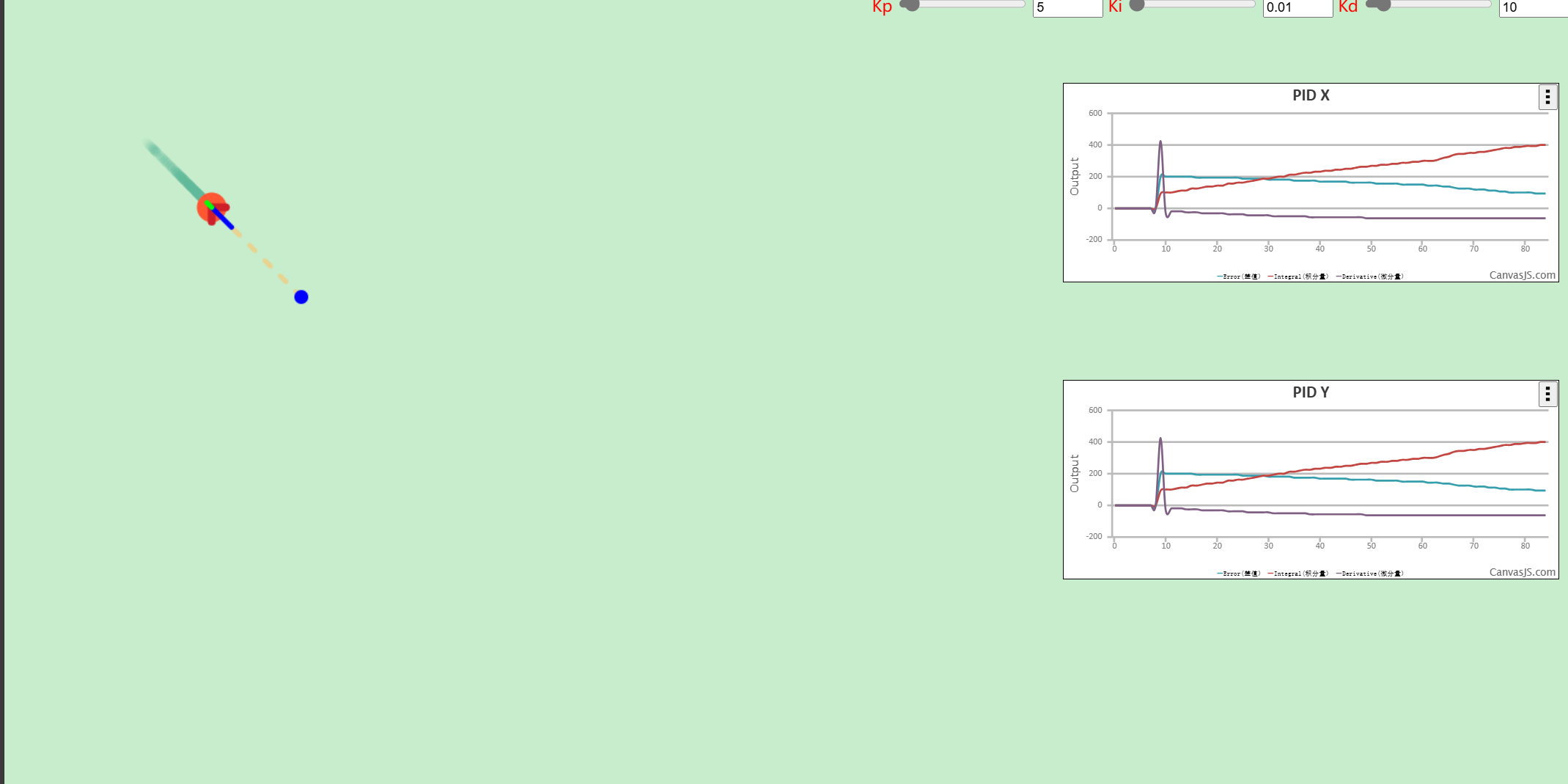
智能控制系统的灵魂：深入研究 PID 控制器的算法逻辑 | Long Luo's Life Notes

使用教程讲述了单级 PID 和串级 PID 的基本实现。可以动态调节参数对小球进行控制 PID Simulator

PID 小球

PID Balancer | PID 平衡车

控制器分类 ¶

P¶

PD¶

PI¶

PID¶

性能分析 ¶

抗扰性能 | Load Response ¶

跟踪性能 | Setpoint Response ¶

参数整定 ¶

经验法 ¶

先调整 P，再调整 D，最后看着调整 I

先只使用比例控制，增大 P 系数至系统震荡之后加入微分控制 D 以增大阻尼，抑制震荡，之后再结合系统对响应和静差等具体要求来调节比例 P 和积分 I 系数。

先是比例后积分，最后再把微分加，
曲线振荡很频繁，比例度盘要放大，
曲线漂浮绕大湾，比例度盘往小扳，
曲线偏离回复慢，积分时间往下降，
曲线波动周期长，积分时间再加长，
曲线振荡频率快，先把微分降下来，
动差大来波动慢，微分时间应加长，
理想曲线两个波，前高后低4比1，
一看二调多分析，调节质量不会低。

粗调 KP ¶

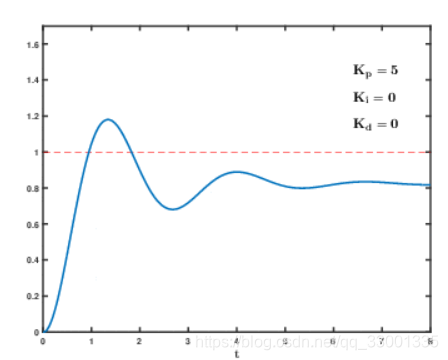
先将积分、微分系数置零，这样系统就是纯比例控制。接着逐渐增大比例系数 P，直至系统出现振荡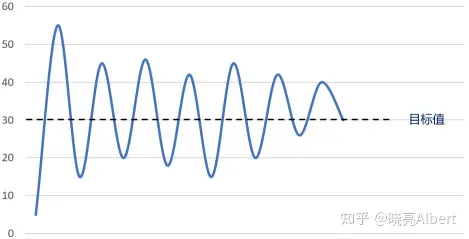；当然，看到上面这个现象，一定要先确认一下系统硬件是否出现问题，比如电机堵转，电压不稳等，先排除硬件问题。

常见现象

水温的保持中表现为温度不断上下浮动，且浮动的频率一定，最大值与最小值相差较小，
在平衡车的调节中会导致平衡车一点点偏角就导致舵机打角程度十分巨大，跑起来就是左右左右不断晃动，但又勉强能跑。

我们可以看到上面比例系数过大，导致系统震荡，超调量很大。接着再逐渐减小比例系数，直至系统振荡消失。

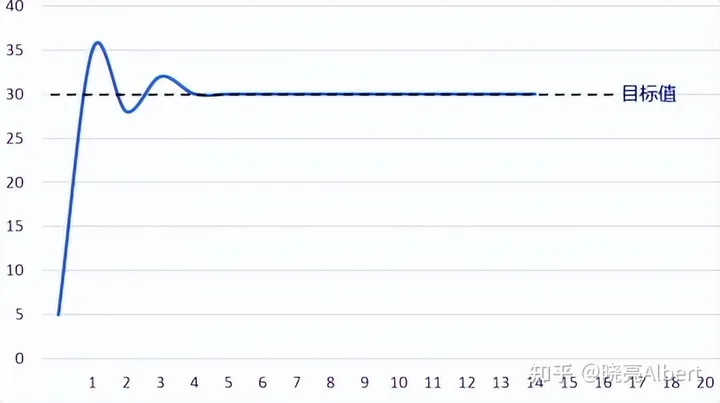
调整 Kd ¶

为了抑制这个小幅度超调，我们逐步增加微分比例系数 D, 直至超调量基本消失，如果此时效果较较佳，就不用考虑引入积分环节。

如上图我们可以看到引入微分环节之后，上升时间很短，超调量没有了，但是出现了静态误差。

现象

当 KP 调好，KI 为零，KD 调节过大时，水温会在达到目标值后猛地上升一下，然后回降一些，平衡车则会在你倾斜车身后猛地打死舵机，然后回过来一点

当你 KD 调好，那是什么情况？那就厉害了，水温可以保持一定温度挺久，平衡车可以跑得动了

调整 Ki ¶

因为有了静态误差，我们就需要逐渐增大积分系数 I，并同时观察曲线的变化，如果消除静差的时间过长，则可以再适当增大积分系数，注意兼顾系统的最大超调量。
如果引入积分项之后系统的又出现微幅度超调，还是要继续增大点微分项来抑制，直至出现较好效果。
在工程实践中，不同的控制系统对控制效果要求不一样，比如平衡车对系统响应速度要求高，控制门窗的开合对快速性不高，但是对稳定性和准确性要求很高。所以我们要根据被控系统要求来调节参数，并不是所有系统都追求所有指标高。

PID 控制参数整定 ( 调参 ) 太高深莫测？一篇文章掌握通用调参思路 - 知乎

经验法 ¶

系统	PB	$ T_i (\text{min}) $	$ T_d (\text{min}) $
温度	20～60	3～10	0.5～3
流量	40～100	0.1～1
压力	30～70	0.4～3
液位	20～80

临界比例法 ¶

① 设置 $\tau_I = \infty$ 和 $\tau_D = 0$，去除积分与微分作用

② 在纯比例作用下，$K_c$ 从小到大逐一尝试，使系统产生等幅振荡

③ 获得临界增益 $K_{cu}$ 和临界振荡周期 $P_{cu}$

④ 根据 Z-N 经验规则，直接查表计算得到 PID 参数

Z-N 经验准则

类型	$ K_c $	$ \tau_I $	$ \tau_D $
P	$ 0.5 \, K_{CU} $
PI	$ 0.45 \, K_{CU} $	$ P_{CU}/1.2 $
PID	$ 0.6 \, K_{CU} $	$ P_{CU}/2 $	$ P_{CU}/8 $

修正 Z-N 经验准则

类型	$ K_c $	$ \tau_I $	$ \tau_D $
标准 ZN	$ 0.6 \, K_{CU} $	$ P_{CU}/2 $	$ P_{CU}/8 $
略有超调	$ 0.33 \, K_{CU} $	$ P_{CU}/2 $	$ P_{CU}/3 $
无超调	$ 0.2 \, K_{CU} $	$ P_{CU}/3 $	$ P_{CU}/2 $

优缺点 ¶

优点

– 不需要过程的先验信息 – 适用于所有稳定的过程

缺点

– 耗时 – 在测试期间会导致产品质量和生产率下降 – 不适用于积分或开环不稳定过程 – 即使控制器增益很大，一阶和二阶无延迟过程也不会振荡

最小化积分误差 ¶

常用的积分误差准则

ISE(Integral Squared Error)
$$ ISE=int_0^infty e(t)^2dt $$

IAE(Integral Average Error)
$$ IAE=int_0^infty|e(t)|dt $$

ITAE(Integral Time Average Error)
$$ ITAE=int_0^infty t|e(t)|dt $$

对于一阶惯性环节

\[ G(s)=\frac{Ke^{-\theta s}}{\tau s+1} \]

抗扰设计跟踪设计

控制器类型	ISE	IAE	ITAE
P	$ K_c = \frac{1.411}{K} (\theta/\tau)^{-0.917} $	$ K_c = \frac{0.902}{K} (\theta/\tau)^{-0.985} $	$ K_c = \frac{0.490}{K} (\theta/\tau)^{-1.084} $
PI	$ K_c = \frac{1.305}{K} (\theta/\tau)^{-0.959} $ $ \tau_I = \frac{\tau}{0.492} (\theta/\tau)^{0.739} $	$ K_c = \frac{0.984}{K} (\theta/\tau)^{-0.986} $ $ \tau_I = \frac{\tau}{0.608} (\theta/\tau)^{0.707} $	$ K_c = \frac{0.859}{K} (\theta/\tau)^{-0.977} $ $ \tau_I = \frac{\tau}{0.674} (\theta/\tau)^{0.680} $
PID	$ K_c = \frac{1.495}{K} (\theta/\tau)^{-0.945} $ $ \tau_I = \frac{\tau}{1.101} (\theta/\tau)^{0.771} $ $ \tau_D = 0.560\tau (\theta/\tau)^{1.006} $	$ K_c = \frac{1.435}{K} (\theta/\tau)^{-0.921} $ $ \tau_I = \frac{\tau}{0.878} (\theta/\tau)^{0.749} $ $ \tau_D = 0.482\tau (\theta/\tau)^{1.137} $	$ K_c = \frac{1.357}{K} (\theta/\tau)^{-0.947} $ $ \tau_I = \frac{\tau}{0.842} (\theta/\tau)^{0.738} $ $ \tau_D = 0.381\tau (\theta/\tau)^{0.995} $

控制器类型	IAE	ITAE
PI	$ K_c = \frac{0.758}{K} (\theta/\tau)^{-0.861} $ $ \tau_I = \frac{\tau}{1.020 - 0.323(\theta/\tau)} $	$ K_c = \frac{0.586}{K} (\theta/\tau)^{-0.916} $ $ \tau_I = \frac{\tau}{1.03 - 0.165(\theta/\tau)} $
PID	$ K_c = \frac{1.086}{K} (\theta/\tau)^{-0.869} $ $ \tau_I = \frac{\tau}{0.740 - 0.130(\theta/\tau)} $ $ \tau_D = 0.348\tau (\theta/\tau)^{0.914} $	$ K_c = \frac{0.965}{K} (\theta/\tau)^{-0.855} $ $ \tau_I = \frac{\tau}{0.796 - 0.147(\theta/\tau)} $ $ \tau_D = 0.308\tau (\theta/\tau)^{0.929} $

Lambda 整定 ¶

根据期望的闭环传递函数，设计 PID 控制器参数

期望的闭环传递函数为 $(Y/R)_d$，因此控制器传递函数 $G_C$ 可以表示为：

\[ G_C = \frac{1}{G} \left( \frac{(Y/R)_d}{1 - (Y/R)_d} \right) \]

数学表达式为：

\[ (Y/R)_d = \frac{e^{-\theta s}}{\tau_c s + 1} \]

这表示对象具有纯滞后特性。

模型	$ K_c $	$ \tau_I $	$ \tau_D $
$ G(s) = \frac{Ke^{-\theta s}}{\tau s + 1} $	$ K_c = \frac{1}{K} \frac{\tau}{\tau_c + \theta} $	$ \tau_I = \tau $
$ G(s) = \frac{Ke^{-\theta s}}{(\tau_1 s + 1)(\tau_2 s + 1)} $	$ K_c = \frac{1}{K} \frac{\tau_1 + \tau_2}{\tau_c + \theta} $	$ \tau_I = \tau_1 + \tau_2 $	$ \tau_D = \frac{\tau_1 \tau_2}{\tau_1 + \tau_2} $

推导

\[ G(s) = \frac{K e^{-\theta s}}{\tau s + 1} \quad \text{及} \quad \left( \frac{Y}{R} \right)_d = \frac{e^{-\theta s}}{\tau_c s + 1} \]

\[ G_c(s) = \frac{\tau s + 1}{K} \cdot \frac{e^{-\theta s}}{\tau_c s + 1 - e^{-\theta s}} \quad \text{(非PID结构)} \]

1 阶泰勒近似 :

\[ e^{-\theta s} \approx 1 - \theta s \]

\[ G_c(s) = \frac{\tau s + 1}{K} \cdot \frac{1}{(\tau_c + \theta) s} = \frac{\tau}{K (\tau_c + \theta)} \left( 1 + \frac{1}{\tau s} \right) \quad \text{(PI)} \]

IMC 整定方法 ¶

内模控制 ( Internal Model Control, 简称 IMC) 是 1982 年由 Garcia 等人提出的，由于它的跟踪调节性能好，鲁棒性强，能消除不可测干扰的影响，设计比较简单，成了一种设计与分析控制系统的有力工具

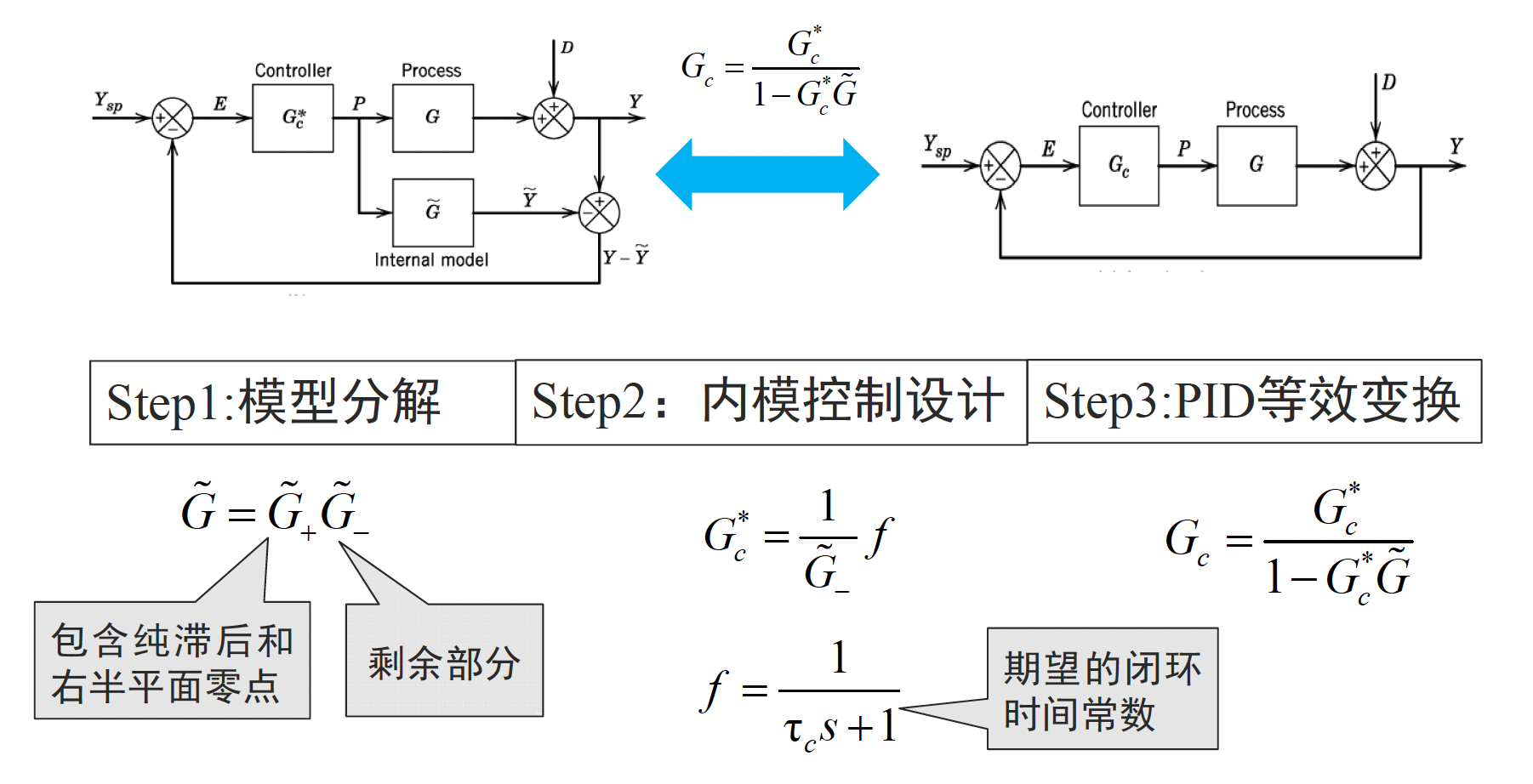
IMC 整定

\[ G(s) = \frac{K e^{-\theta s}}{\tau s + 1} \quad e^{-\theta s} = \frac{1 - 0.5 \theta s}{1 + 0.5 \theta s} \quad \text{(1阶Pade近似)} \]

\[ \tilde{G}_+ = 1 - 0.5 \theta s \quad \tilde{G}_- = \frac{K}{(\tau s + 1)(1 + 0.5 \theta s)} \]

\[ G_c^* = \frac{1}{\tilde{G}_-} f = \frac{(\tau s + 1)(1 + 0.5 \theta s)}{K (\tau_c s + 1)} \]

\[ G_c = \frac{G_c^*}{1 - G_c^* \tilde{G}} = \frac{(\tau s + 1)(1 + 0.5 \theta s)}{K (\tau_c + 0.5 \theta) s} \quad \text{(PID)} \]

\[ K_c = \frac{1}{K} \frac{(\tau + \theta / 2)}{(\tau_c + \theta / 2)} \quad \tau_I = \tau + \theta / 2 \quad \tau_D = \frac{\tau \theta / 2}{\tau + \theta / 2} \]

优化 ¶

PID 的 TRICK( 一 ) 简述五种 PID 积分抗饱和（ANTI-Windup）方法 - 知乎史上最详细的PID教程——理解PID原理及优化算法_串级pid为什么可以减小稳定时间-CSDN博客

积分优化 ¶

积分饱和｜ Anti-Windup

如果系统总是存在统一的方向偏差，就可能无限累加而进行饱和，极大影响系统性能

所谓积分饱和就是指系统存在一个方向的偏差，PID 控制器的输出由于积分作用的不断累加而扩大，从而导致控制器输出不断增大超出正常范围进入饱和区。当系统出现反响的偏差时，需要首先从饱和区退出，而不能对反向的偏差进行快速的响应。

积分分离或者称为去积分算法，变速积分（积分项和误差相映射）；
在饱和的时候将积分器的累计值初始化到一个比较理想的值；
若积分饱和因为目标值突然变化而产生，将目标值以适当斜率的斜坡变化可避免此情形；
将积分累计量限制上下限，避免积分累计量超过限制值；
如果 PID 输出已经饱和，重新计算积分累计量，使输出恰好为合理的范围；

积分分离 ¶

基本思想

在系统误差较大时，取消积分环节
当误差较小时，引入积分环节
这样既不影响控制器的动态性能，又可以提高控制器的稳态精度

积分分离控制算法可表示为：

\[ u(k) = K_p e(k) + a K_1 \sum_{i=1}^{k-1} e(i) + K_D [e(k) - e(k-1)] \]

$T$ 为采样时间
$a$ 为积分项的开关系数，$a$ 的函数也可以分成三段。或者设置为某种函数，误差大时积分系数小，误差小时积分系数大，这就是变速积分的思想
$$ a = begin{cases} 1 & |e(k)| leqslant varepsilon \ 0 & |e(k)| > varepsilon end{cases} $$

反馈抑制抗饱和（back-calculation）¶

基本思想

当饱和时，对积分项加入负反馈，使其尽快退出饱和。

其中 $K_b$ 设置的范围为 $0.3\sim3*\frac{K_i}{K_p}$，默认的为 $\frac{K_i}{K_p}$ 即可

饱和程度的不同来调节反馈系数，饱和程度越深，反馈系数越大。

变速积分 ¶

系统对于积分项的要求是，系统偏差大时，积分作用应该减弱甚至是全无，而在偏差小时，则应该加强。积分系数取大了会产生超调，甚至积分饱和，取小了又不能短时间内消除静差。因此，根据系统的偏差大小改变积分速度是有必要的。变积分 PID 的基本思想是设法改变积分项的累加速度，使其与偏差大小相对应：偏差越大，积分越慢 ; 偏差越小，积分越快。

梯形积分 ¶

微分优化 ¶

不完全微分 ¶

突然来一个阶跃信号，会导致微分项很大，导致控制器输出很大，进而导致系统震荡。

不完全的微分它使得在偏差作阶跃式变化时出现的输出瞬时跳变得到一定程度的缓和，因而在实际的 PID 控制算法中得到广泛采用。在 PID 控制中，微分信号的引入可以改善系统的动态特性，但也易引入高频干扰，在误差扰动突变的时候尤其显出微分项的不足。要想解决这个问题，可以在控制算法中加入低通滤波器

微分先行 ¶

某些给定值频繁且大幅变化的场合，微分项常常会引起系统的振荡。为了适应这种给定值频繁变化的场合，人们设计了微分先行算法。

类似于不完全微分（不完全微分是通过削弱变化量来尽可能的实现完全响应，而微分先行 PID 控制是只对输出量进行微分，而对给定指令不起微分作用），微分部分只与测量值有关，而且与连续的几个测量值都有关。而与设定值没有关系，设定值的阶跃变化不会造成高频的干扰。

其他优化 ¶

设定值响应 ¶

带死区 ¶

带死区

在偏差小到一点程度时 PID 不起作用

PID 控制器开发笔记之八：带死区的 PID 控制器的实现 _ 木南创智 -CSDN 博客

在计算机控制系统中，由于系统特性和计算精度等问题，致使系统偏差总是存在，系统总是频繁动作不能稳定。为了解决这种情况，我们可以引入带死区的 PID 算法。

带死区的 PID 控制算法就是检测偏差值，若是偏差值达到一定程度，就进行调节。若是偏差值较小，就认为没有偏差。用公式表示如下：

\[ u(k) = \begin{cases} u(k-1) & |e(k)| \leqslant \Delta \\ u(k-1) + K_p (e(k) - e(k-1)) & |e(k)| > \Delta \end{cases} \]

其中的死区值得选择需要根据具体对象认真考虑，因为该值太小就起不到作用，该值选取过大则可能造成大滞后。

带死区的 PID 算法，对无论位置型还是增量型的表达式没有影响，不过它是一个非线性系统。

除以上描述之外还有一个问题，在零点附近时，若偏差很小，进入死区后，偏差置 0 会造成积分消失，如是系统存在静差将不能消除，所以需要人为处理这一点。

引入死区的主要目的是消除稳定点附近的波动，由于测量值的测量精度和干扰的影响，实际系统中测量值不会真正稳定在某一个具体的值，而与设定值之间总会存在偏差，而这一偏差并不是系统真实控制过程的反应，所以引入死区就能较好的消除这一点。

当然，死区的大小对系统的影响是不同的。太小可能达不到预期的效果，而太大则可能对系统的正常变化造成严重滞后，需要根据具体的系统对象来设定。

类型	\( K_c \)	\( \tau_I \)	\( \tau_D \)
P	\( 0.5 \, K_{CU} \)
PI	\( 0.45 \, K_{CU} \)	\( P_{CU}/1.2 \)
PID	\( 0.6 \, K_{CU} \)	\( P_{CU}/2 \)	\( P_{CU}/8 \)

类型	\( K_c \)	\( \tau_I \)	\( \tau_D \)
标准 ZN	\( 0.6 \, K_{CU} \)	\( P_{CU}/2 \)	\( P_{CU}/8 \)
略有超调	\( 0.33 \, K_{CU} \)	\( P_{CU}/2 \)	\( P_{CU}/3 \)
无超调	\( 0.2 \, K_{CU} \)	\( P_{CU}/3 \)	\( P_{CU}/2 \)

控制器类型	ISE	IAE	ITAE
P	\( K_c = \frac{1.411}{K} (\theta/\tau)^{-0.917} \)	\( K_c = \frac{0.902}{K} (\theta/\tau)^{-0.985} \)	\( K_c = \frac{0.490}{K} (\theta/\tau)^{-1.084} \)
PI	\( K_c = \frac{1.305}{K} (\theta/\tau)^{-0.959} \) \( \tau_I = \frac{\tau}{0.492} (\theta/\tau)^{0.739} \)	\( K_c = \frac{0.984}{K} (\theta/\tau)^{-0.986} \) \( \tau_I = \frac{\tau}{0.608} (\theta/\tau)^{0.707} \)	\( K_c = \frac{0.859}{K} (\theta/\tau)^{-0.977} \) \( \tau_I = \frac{\tau}{0.674} (\theta/\tau)^{0.680} \)
PID	\( K_c = \frac{1.495}{K} (\theta/\tau)^{-0.945} \) \( \tau_I = \frac{\tau}{1.101} (\theta/\tau)^{0.771} \) \( \tau_D = 0.560\tau (\theta/\tau)^{1.006} \)	\( K_c = \frac{1.435}{K} (\theta/\tau)^{-0.921} \) \( \tau_I = \frac{\tau}{0.878} (\theta/\tau)^{0.749} \) \( \tau_D = 0.482\tau (\theta/\tau)^{1.137} \)	\( K_c = \frac{1.357}{K} (\theta/\tau)^{-0.947} \) \( \tau_I = \frac{\tau}{0.842} (\theta/\tau)^{0.738} \) \( \tau_D = 0.381\tau (\theta/\tau)^{0.995} \)

模型	\( K_c \)	\( \tau_I \)	\( \tau_D \)
\( G(s) = \frac{Ke^{-\theta s}}{\tau s + 1} \)	\( K_c = \frac{1}{K} \frac{\tau}{\tau_c + \theta} \)	\( \tau_I = \tau \)
\( G(s) = \frac{Ke^{-\theta s}}{(\tau_1 s + 1)(\tau_2 s + 1)} \)	\( K_c = \frac{1}{K} \frac{\tau_1 + \tau_2}{\tau_c + \theta} \)	\( \tau_I = \tau_1 + \tau_2 \)	\( \tau_D = \frac{\tau_1 \tau_2}{\tau_1 + \tau_2} \)

控制器类型	IAE	ITAE
PI	\( K_c = \frac{0.758}{K} (\theta/\tau)^{-0.861} \) \( \tau_I = \frac{\tau}{1.020 - 0.323(\theta/\tau)} \)	\( K_c = \frac{0.586}{K} (\theta/\tau)^{-0.916} \) \( \tau_I = \frac{\tau}{1.03 - 0.165(\theta/\tau)} \)
PID	\( K_c = \frac{1.086}{K} (\theta/\tau)^{-0.869} \) \( \tau_I = \frac{\tau}{0.740 - 0.130(\theta/\tau)} \) \( \tau_D = 0.348\tau (\theta/\tau)^{0.914} \)	\( K_c = \frac{0.965}{K} (\theta/\tau)^{-0.855} \) \( \tau_I = \frac{\tau}{0.796 - 0.147(\theta/\tau)} \) \( \tau_D = 0.308\tau (\theta/\tau)^{0.929} \)

PID 控制 ¶

建模 ¶

连续系统 ¶

离散 - 位置式 PID ¶

离散 - 增量式 PID ¶

对比 ¶

结构形式 ¶

可视化 ¶

控制器分类 ¶

P¶

PD¶

PI¶

PID¶

性能分析 ¶

抗扰性能 | Load Response ¶

跟踪性能 | Setpoint Response ¶

参数整定 ¶

经验法 ¶

粗调 KP ¶

调整 Kd ¶

调整 Ki ¶

经验法 ¶

临界比例法 ¶

优缺点 ¶

最小化积分误差 ¶

Lambda 整定 ¶

IMC 整定方法 ¶

优化 ¶

积分优化 ¶

积分分离 ¶

反馈抑制抗饱和（back-calculation）¶

变速积分 ¶

梯形积分 ¶

微分优化 ¶

不完全微分 ¶

微分先行 ¶

其他优化 ¶

设定值响应 ¶

带死区 ¶

应用 ¶

单级 PID ¶

串级 PID ¶

低通滤波 + PID ¶

前馈补偿 PID ¶