MPC 控制 ¶
约 5197 个字 197 行代码 10 张图片 预计阅读时间 23 分钟
指的是通过模型预测系统在某一未来时间段的表现,进而优化控制量
多用于数位控制,离散时间系统
别名:
- 开环最优反馈
- 反应式规划
- Receding Horizon Control | 滚动优化控制
- 考虑未来时域
- 考虑误差
- 减少问题规模
- 计算量大
- 需要在线求解
Acknowledgement¶
- DR_CAN 【MPC 模型预测控制器】系列课程
- 笔记部分参考了 colaforced/ControlTheoryNote
DMC 部分
是什么 ¶
在 \(k\) 时刻
- 估计 / 测量得到当前状态值(无法测量的话,设计观测器)
- 基于 \(u(k), u(k+1), \cdots, u(k+N-1)\) 进行优化
- Cost Function:\(J = \sum_{i=k}^{k+N-1} (E_i^T Q E_i + U_i^T R U_i) + E_N^T F E_N\)
- \(F\) 是终端惩罚 ,Terminal cost
- 预测区间:\(\left[y(k+1), y(k+2), \cdots, y(k+N-1)\right]\)
- 控制区间:\(\left[u(k), u(k+1), \cdots, u(k+N-1)\right]\)
- N 是预测时域 prediction horizon
- Cost Function:\(J = \sum_{i=k}^{k+N-1} (E_i^T Q E_i + U_i^T R U_i) + E_N^T F E_N\)
- 在输出的时候,只执行 \(u(k)\) 这一个控制量
- 将预测区间和控制区间后移一个时刻,重复上述过程
约束项 : 包括等式约束或者不等式约束,比如避障约束
fix horizon,N 是固定的 预测时间和计算量是一个balance
重点
- 解十个指令,只执行 1 个指令
- 每个状态都可以有当前状态 \(x(k)\), 进行前向积分求得
terminal cost
不想指定最后 terminal cost 而不加的话,有可能不动
所以加一个正则项,让他动起来
线性有约束或者非线性有约束需要一些人为的约束
无约束 MPC = 线性反馈控制
一个线性无约束的 MPC 解析最优解是一个关于初值的最优反馈
如何建模 ¶
我们的任务是最小化代价函数。
其中 - \(X_{(k+i|k)}\) 表示在\(k\)时刻预测的\(k+i\)时刻的状态 - \(U_{(k+i|k)}\) 表示在\(k\)时刻预测的\(k+i\)时刻的控制量 - \(Q\) 是状态的权重矩阵 - \(R\) 是控制量的权重矩阵 - \(F\) 是终端惩罚
这个方程当中,有 \(X_{(k+i|k)}\) 和 \(U_{(k+i|k)}\) 两个变量,我们又知道对于二次型函数的优化
已经有成熟的方法,所以,我们的目的就是把原有的代价函数,变化到只包含当前状态量 \(x(k)\)(常数)和控制量 \(u(k)\) 的函数,只有一个变量之后,就可以套用二次规划的方法求解了。
先做一些声明:
状态量:
控制量:
- \(X_{(k|k)} = X_k\) 表示初始状态
- \(X_{(k+1|k)}\) 则是根据模型和 \(U_{(k|k)}, X_k\) 计算出来的
- \(X_{(k+1|k)}, ..., X_{(k+N|k)}\) 是进一步迭代计算得到的
研究的是离散形式的状态空间表达式
把状态空间表达式展开,写成方程组的形式
可以化简成矩阵的形式(对应元素使用相同颜色进行标注)
回顾公式 \(J\),我们也可以使用矩阵对于求和项进行化简
带入刚才求得的 \(\hat{X}_k = M\hat{X}_k + C\hat{U}_k\)
可以得到
所以最后推导出的代价函数形式:
此时我们的目标是通过最小化 \(J\),来求解 \(\hat{U}_k\),而 \(\hat{X}_k\) 是已知的,与优化过程无关
观察可得,\(2\hat{X}_k^T E \hat{U}_k\) 是一个关于 \(\hat{U}_k\) 的线性项,\(\hat{U}_k^T H \hat{U}_k\) 是一个关于 \(\hat{U}_k\) 的二次型,可以套用二次规划的方法求解
这里也可以直接对 \(J\) 求梯度
注意向量求导法则
所以最优的控制量是一个关于初值 \(X_k\) 的线性反馈
所以无约束 MPC 其实等价于线性反馈控制(linear feedback control)
整理 ¶
最后,我们来整理一下整个求解过程当中遇到的矩阵以及它们的维度
B 是 \(n \times p\) 的矩阵,AB 也是 \(n \times p\) 的矩阵
代码实现 ¶
核心公式
- \(E = C^T \bar{Q} M,\quad H = C^T \bar{Q} C + \bar{R}\)
所以,计算 \(E\) 和 \(H\) 需要 \(A,B,Q,R,F,N\)
- \(C\):\(A,B\)
- \(M\):\(A\)
- \(\bar{Q}\):\(Q,F\)
- \(\bar{R}\):\(R\)
clear ;
close all;
clc;
%% 第一步,定义状态空间矩阵
A = [1 0.1; -1 2]; %% 定义状态矩阵 A, n x n 矩阵
n= size (A,1);
B = [ 0.2 1; 0.5 2]; %% 定义输入矩阵 B, n x p 矩阵
p = size(B,2);
Q=[100 0;0 1]; %% 定义Q矩阵,n x n 矩阵
F=[100 0;0 1]; %% 定义F矩阵,n x n 矩阵
R=[1 0 ;0 .1]; %% 定义R矩阵,p x p 矩阵
k_steps=100; %% 定义step数量k
X_K = zeros(n,k_steps); %% 定义矩阵 X_K, n x k 矩 阵
X_K(:,1) =[20;-20]; %% 初始状态变量值, n x 1 向量
U_K=zeros(p,k_steps); %% 定义输入矩阵 U_K, p x k 矩阵
N=5; %% 定义预测区间K
[E,H]=MPC_Matrices(A,B,Q,R,F,N); %% Call MPC_Matrices 函数 求得 E,H矩阵
%% 计算每一步的状态变量的值
for k = 1 : k_steps
%% 求得U_K(:,k)
U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);
%% 计算第k+1步时状态变量的值
X_K(:,k+1)=(A*X_K(:,k)+B*U_K(:,k));
end
%% 绘制状态变量和输入的变化
subplot (2, 1, 1);
hold;
for i =1 :size (X_K,1)
plot (X_K(i,:));
end
legend("x1","x2")
hold off;
subplot (2, 1, 2);
hold;
for i =1 : size (U_K,1)
plot (U_K(i,:));
end
legend("u1","u2")
function [E,H]=MPC_Matrices(A,B,Q,R,F,N)
n = size(A,1); % A 是 n x n 矩阵, 得到 n
p = size(B,2); % B 是 n x p 矩阵, 得到 p
%% 定义M和C
M = [eye(n);zeros(N*n,n)]; % 初始化 M 矩阵. M 矩阵是 (N+1)n x n的, 它上面是 n x n 个 "I", 这一步先把下半部分写成 0
C = zeros((N+1)*n,N*p); % 初始化 C 矩阵, 这一步令它有 (N+1)n x NP 个 0
tmp = eye(n); %定义一个n x n 的 I 矩阵
%% 更新M和C
for i=1:N % 循环,i 从 1到 N
rows = i*n+(1:n); %定义当前行数,从i x n开始,共n行
C(rows,:) = [tmp*B,C(rows-n, 1:end-p)]; %将c矩阵填满
tmp = A*tmp; %每一次将tmp左乘一次A
M(rows,:) = tmp; %将M矩阵写满
end
%% 定义Q_bar和R_bar
Q_bar = kron(eye(N),Q);
Q_bar = blkdiag(Q_bar,F);
R_bar = kron(eye(N),R);
%% 计算G, E, H
G = M'*Q_bar*M; % G: n x n
E = C'*Q_bar*M; % E: NP x n
H = C'*Q_bar*C+R_bar; % NP x NP
end
function u_k= Prediction(x_k,E,H,N,p)
U_k = zeros(N*p,1); % NP x 1
U_k = quadprog(H,E*x_k);
u_k = U_k(1:p,1); % 取第一个结果
end
算法 - DMC ¶
基于阶跃响应的动态矩阵控制 | Dynamic Matrix Control
DMC 算法包括预测模型、滚动优化和反馈校正三个部分组成
参考资料 【预测控制3】动态矩阵控制(DMC)及Matlab仿真-CSDN博客 动态矩阵控制(DMC)的简单理解及其示例-CSDN博客
预测模型 ¶
DMC 算法采用阶跃响应序列作为预测模型
- 假设对象的单位阶跃响应值为 \(a_i (i=1,2\dots N)\),且在 \(N\) 个采样周期后趋于平稳,即 \(a_i \approx a(\infty)\)
- 那么如果我们知道了这些阶跃响应值,就相当于知道了对象的模型参数,所有有限集合 \(a^T = [a_1,a_2,\dots,a_N]\) 可以完全描述系统动态特性
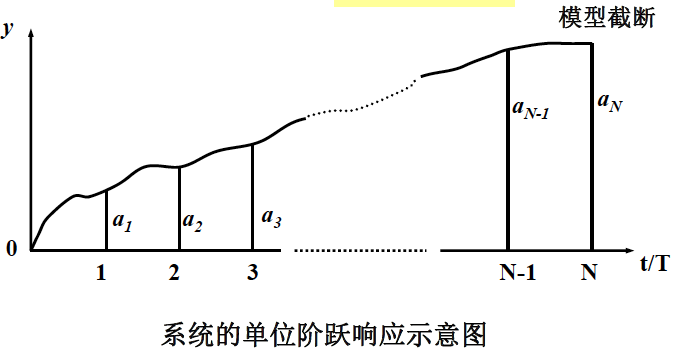
- LTI 系统有叠加性
Phil 减肥的例子
假设我们有一个简单的减肥计划,目标是将 Phil 的体重从当前水平降低到设定的目标体重。阶跃响应在这里可以理解为:当我们突然将 Phil 的每日卡路里摄入量从一个固定值减少到一个较低值时,体重随时间的变化情况。
在 DMC 中,我们会观察 Phil 的体重如何随着时间逐渐下降,直到达到一个新的稳定状态。这个过程中的体重变化曲线就是阶跃响应。通过分析这个响应,我们可以预测在不同时间点的体重变化,从而更好地控制卡路里摄入量,使体重达到并保持在目标值。
例如,如果我们知道在卡路里摄入量恒定减少的情况下,Phil 的体重在一周后下降了 1 公斤,那么我们可以利用这个信息来预测未来的体重变化,并调整控制策略以实现最佳的体重控制。
相当于在我们推导的式子当中,\(A\) 是单位矩阵,\(B\) 是 \(a_i\)
滚动优化 ¶
即计算最优控制序列 \(u_k,u_{k+1},\dots,u_{k+N-1}\)
我们的目标:
- 让输出预测值在 P 时刻尽可能接近参考值 \(\omega_{k+i}\)
- 且输入量 \(\Delta u(k), \dots, \Delta u(k+M-1)\) 不要太大
设计目标函数:
例子:小明的增肥计划,小明根据自己的模型向量 \(a\),计划 5 天分布增加饭量 \(\Delta u(1),....,\Delta u(5)\),然后预测接下 7 天的体重,让其尽可能的接近 120 斤。这里的 5 天相当于控制时域,7 天相当于优化时域。那么如何求出 \(\Delta u(1),....,\Delta u(5)\) 的最优值呢?
直接套用我们之前推过的公式
则控制量选取
又因为我们上面发现,无约束的 MPC 等价于线性反馈控制,所以我们可以直接用线性反馈控制来校正
反馈校正 ¶
在时刻 \(t = kT\),已经计算出控制增量 \(\Delta u(k)\),并施加于被控对象上。
在时刻 \(t = (k+1)T\),可以测量到实际输出值 \(y(k+1)\),并将其与预测值 \(\hat{y}_{1}(k+1/k)\) 进行比较:
经过误差校正后的输出预测值为:
其中,\(\mathbf{h} = [h_{1} \quad h_{2} \quad \cdots \quad h_{N}]^{T}\) 是误差校正向量,用于对不同时刻的预测值进行校正时所加的权重系数。
在时刻 \((k+1)T\) 的预测初值 \(Y_{N0}(k+1)\) 为:
参数整定 ¶
-
根据对象类型和动态特性确定采样周期,测试相应采样周期下经光滑之后的阶跃响应系数 \(a_i\)。
-
取优化时域 \(P\) 覆盖阶跃响应的主要动态部分,而不要求取到阶跃响应的动态变化结束。初选 \(P\) 之后,输出偏差加权系数 \(q_i = 0\)(时滞和反向部分
) ,\(q_i = 1\)(其他部分) 。 -
对简单动态对象,取控制时域 \(M = 1 \sim 2\),对于包括振荡的动态复杂对象,可适当增加 \(M\),取 \(4 \sim 8\);初选 \(R = 0\)。
-
计算控制系数 \(\mathbf{d_i}\),进行仿真,检验控制系统的动态响应。若不稳定或动态过于缓慢,可调整 \(P\),直到满意为止。
-
若上述满意控制的控制量变化幅度较大,可加大 \(R\) 值。
-
在上述参数的基础上,根据控制要求的侧重点,选择校正参数 \(h\),兼顾鲁棒性和抗干扰性的要求。
采样周期 T & 模型长度 N ¶
T 的选择一般应遵循一般采样控制中对采样周期的选择原则,即 必须满足香农定理(采样频率>2倍的截止频率)。 - 对于单容对象,可取\(T\leq 0.1T_a\),\(T_a\)是指对象的惯性时间常数 - 对于振荡对象,可取\(T\leq 0.1T_e\),\(T_e\)指振荡周期 - 对于滞后对象,可取\(T\leq 0.25T_t\),\(T_t\)指对象的纯滞后时间
| 采样周期 \(T\) | 影响 |
|---|---|
| \(T \downarrow\) | \(N \uparrow\),计算频率加大,计算量增大,影响实时性,特别在有约束情况下;但有利于快速抑制干扰。 |
| \(T \uparrow\) | 丢失高频信息,无法构造连续时间信号,模型不准确,控制品质下降。 |
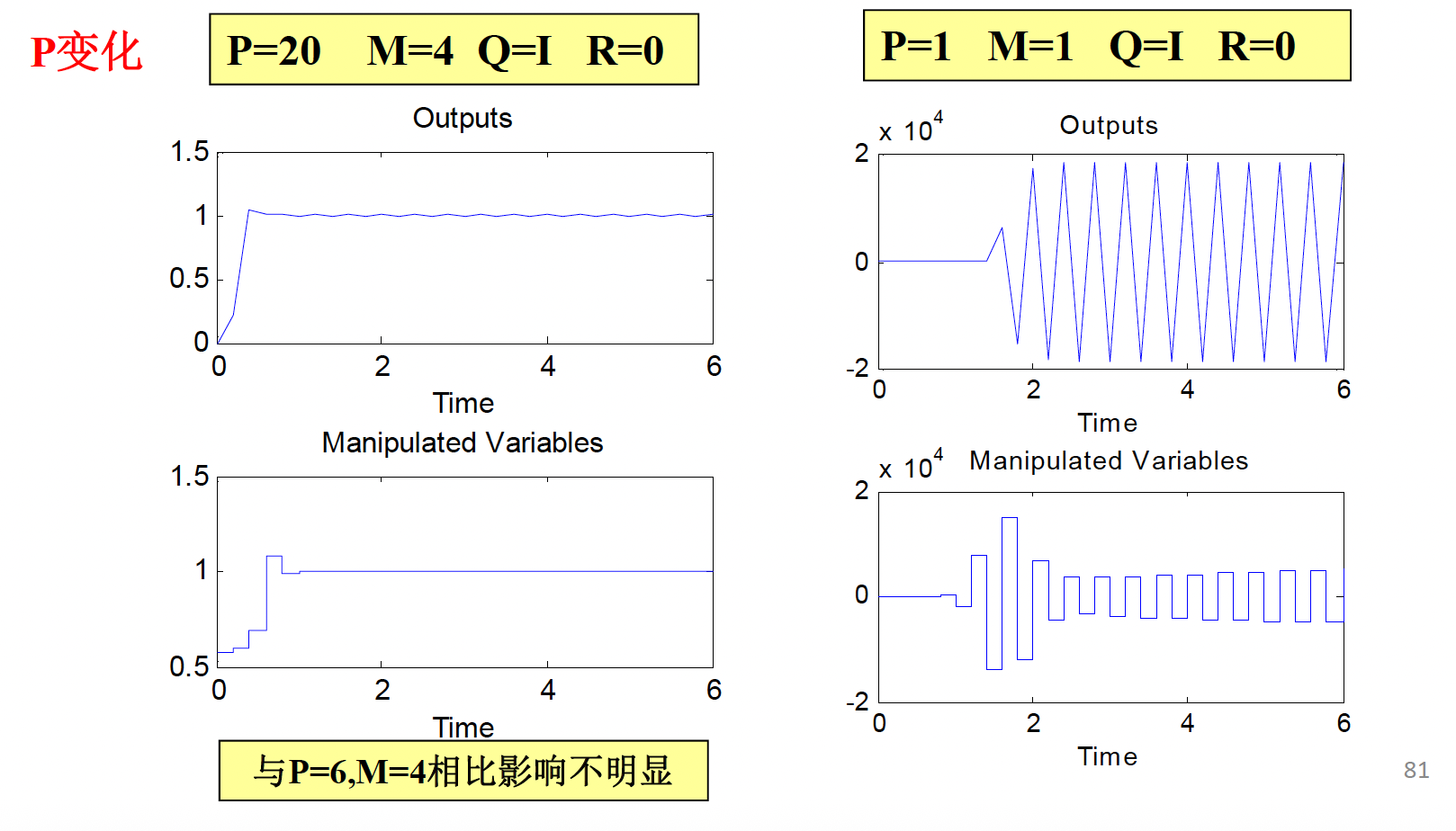
优化时域 P ¶
\(P\) 表示我们对 \(k\) 时刻起未来多少步的输出预测值逼近期望值感兴趣。为了使滚动优化真正有意义,要求优化的范围包含对象的真实动态部分。
优化时域 \(P\) 必须超过对象阶跃响应的时滞部分,或非最小相位引起的反向部分,并覆盖对象的主要动态部分。
通常,\(P\) 取在达到对象阶跃响应稳态值 \(80\%\)~\(90\%\) 的时域范围里
| 优化时域 \(P\) | 优势 | 劣势 |
|---|---|---|
| \(P\) 小 | 快速性好 | 稳定性和鲁棒性差 |
| \(P\) 大 | 稳定性好 | 动态响应慢,增加计算时间,降低系统实时性 |
控制时域 M ¶
控制时域 \(M\) 在优化性能指标中表示所要确定的未来控制量改变的数目,\(M<P\)。
用 \(M\) 个优化变量实现 \(P\) 个点的输出优化,从物理意义上讲,就是把 \(P\) 个点优化的要求分担到 \(M\) 个优化变量上。
一般情况下,\(M\) 越小,则越难保证输出在各采样点紧跟期望值的变化,所得到的性能指标也越差。
| 控制时域 \(M\) | 优点 | 缺点 |
|---|---|---|
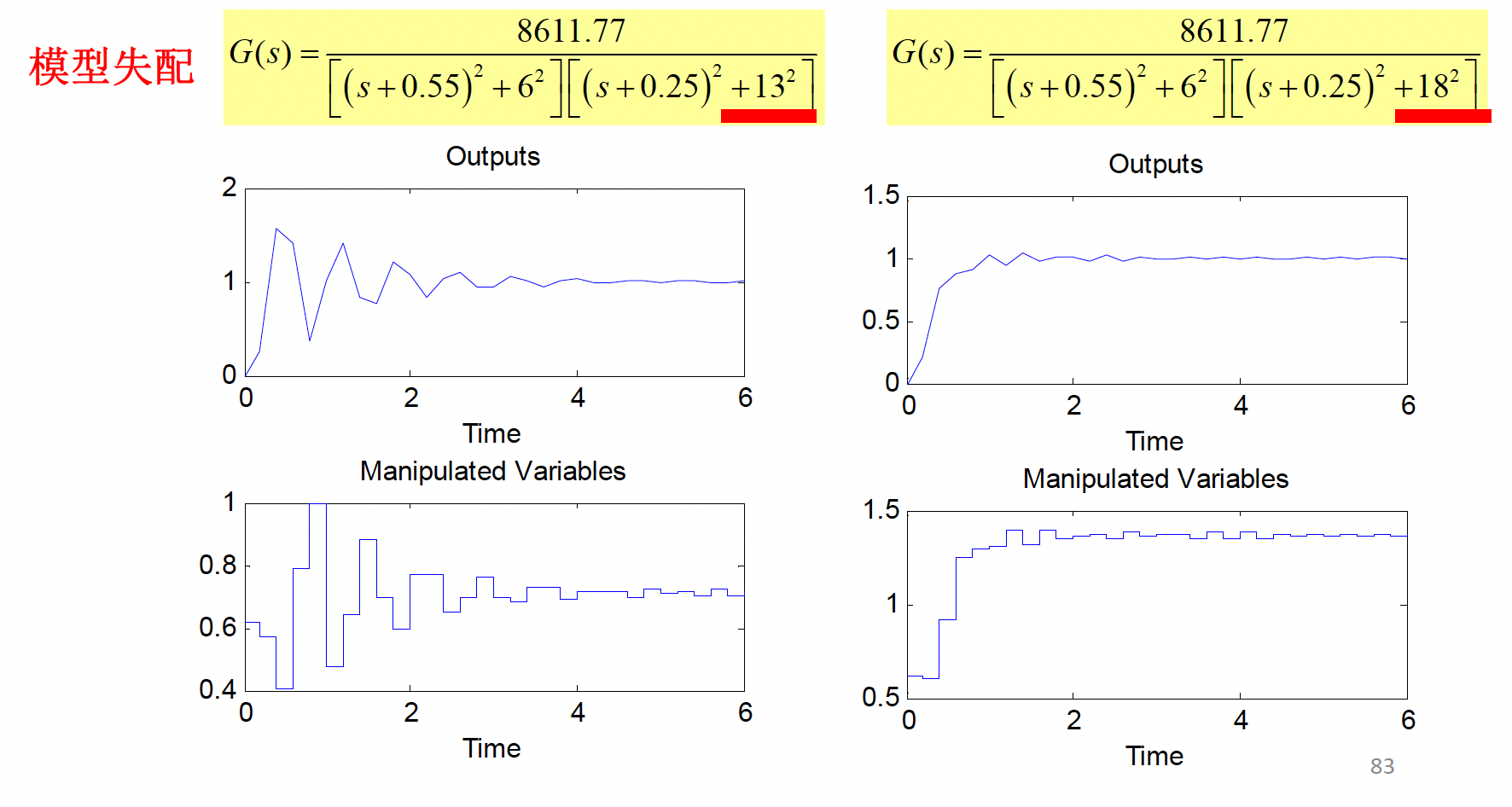
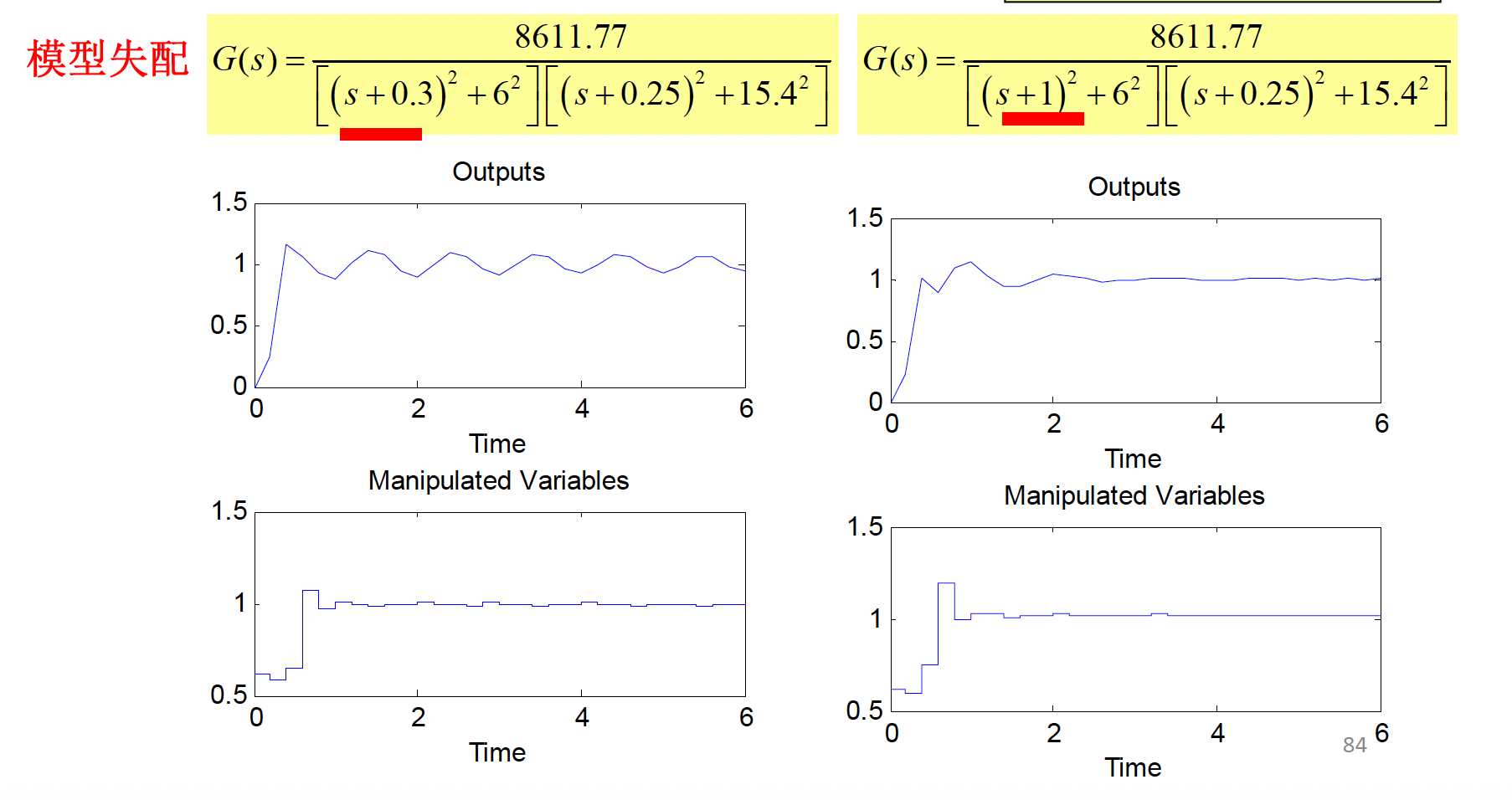
| \(M\) 小 | 容易导致稳定的控制,并对模型失配有较好的鲁棒性 | 控制的机动性较弱,优化要求只能在总体上得到平均兼顾 |
| \(M\) 大 | 控制的机动性较强,有可能改善动态响应 | 提高了控制的灵敏度,其稳定性和鲁棒性变差,增加了计算时间,降低了实时性 |
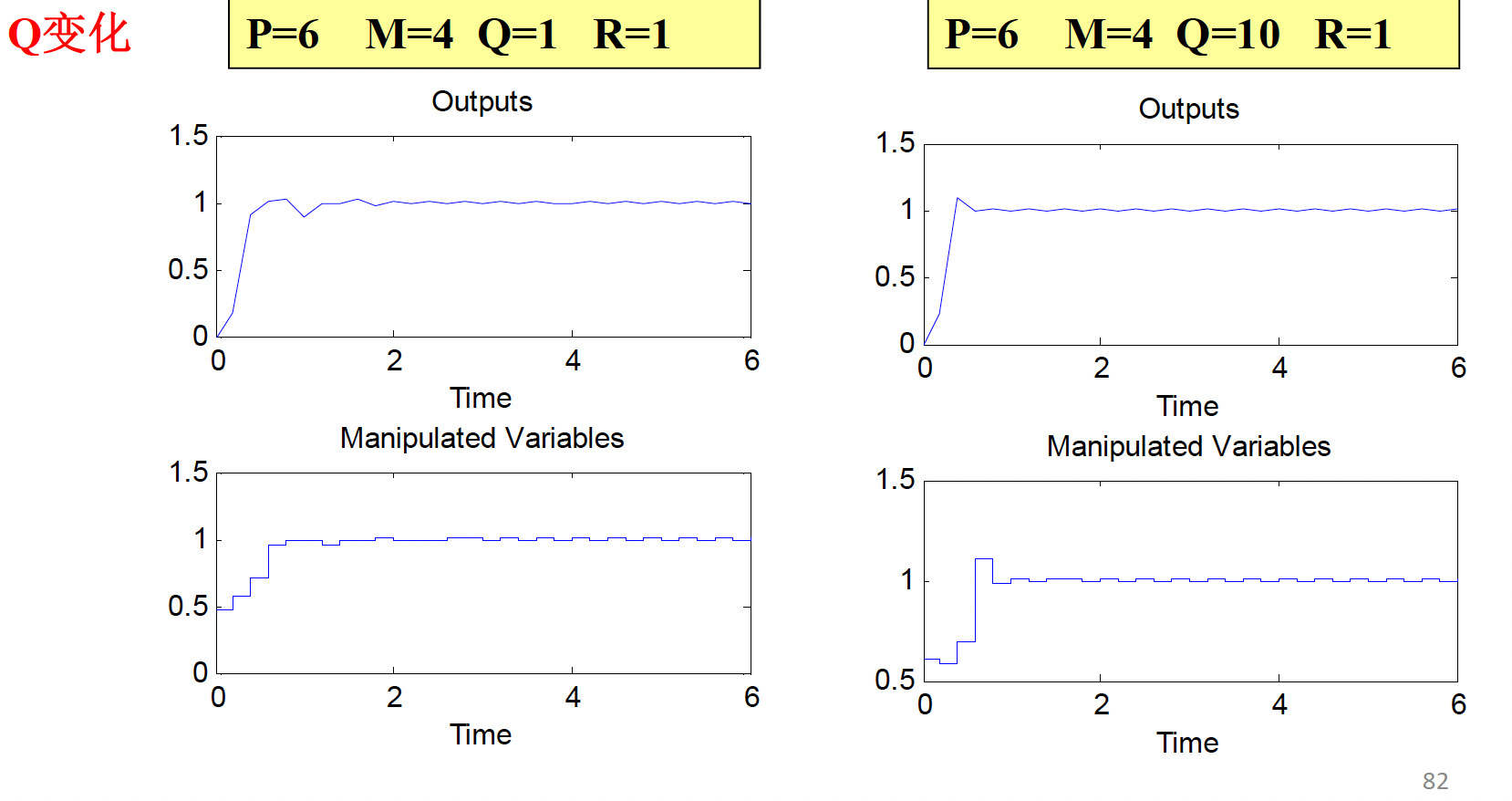
输出偏差加权 Q ¶
权系数 \(q_i\) 的大小反映了优化性能指标中不同时刻对预测输出逼近期望值的重视程度 .
对于时滞和因非最小相位特性引起的反向部分,应取为 0,即 \(q_i= 0\) \((i< N_1)\),\(N_1\) 表示系统时滞或反向部分。
一般地:
控制增量加权阵 R ¶
控制增量加权阵通常选为对角阵 \(diag( r_1, r_2, . . . , r_M)\)
目的:
1) 对控制增量的剧烈变化加以适度限制,减少对系统过大的冲击
2) 改善矩阵 \(A^TQA+ R\) 的条件数 Condition Number
理论分析证明:R 对稳定性的影响不是单调的
对于一阶对象,充分大和充分小的 R 均可以导致无振荡的控制,但对于 R 的某一中间区域,被控系统是以振荡形式收敛的; 对于二阶对象,虽然R在充分大和充分小时都能得到稳定的控制,但R的某一中间区域却会使控制系统振荡发散。 对R的调整,着眼点不应放在控制系统稳定性上,这部分要求通过调整P和M得到满足。
校正参数 h ¶
误差校正向量 \(\mathbf{h}\) 仅在对象收到未知干扰和存在模型失配,造成预测输出和实际输出不一致时才起作用,而对控制的动态响应没有明显的影响。
校正参数的不同选择对系统的抗干扰性和鲁棒性有不同的影响。
- 当 \(h_{i}\) 较小时,反馈校正较弱,鲁棒性增强,但对抗动的敏感性降低,抗干扰性较差。
- 当 \(h_{i}\) 较大时,反馈校正较强,鲁棒性减弱,但对抗动的敏感性增强,抗干扰性较强。
校正参数的取法包括:
- 等值修正: \(h_{1}=1\),\(h_{i}=\alpha\),其中 \(i=2\cdots N\)。
- 衰减修正: \(h_{1}=1\),\(h_{i}=\alpha^{i-1}\),其中 \(i=2\cdots N\)。
- 递增修正: \(h_{1}=1\),\(h_{i+1}=h_{i}+\alpha^{i}\),其中 \(i=2\cdots N\)。
校正参数的选择应在鲁棒性和抗干扰性之间取得平衡。
案例 ¶
最小相位对象
对象的阶跃响应表达式为:
对象的阶跃响应图
- 稳态值 : 1 最大超调 : 0.93
- 调节时间 : 6.4s
- 弱阻尼振荡最小相位系统
取
- 采样时间为 : 0.2s
- 模型长度 N: 40
- 优化时域 P: 6 ( 使系统至少经历一个振荡周期

代码 ¶
该对象具有以下特性:
- 包含纯滞后环节 \(e^{-1.5s}\),滞后时间为 1.5 秒
- 包含非最小相位环节 \((-6s + 1)\),表明系统初始响应方向与最终响应方向相反
- 包含两个惯性环节,时间常数分别为 20 秒和 5 秒
% Start of Selection
clear all;
close all;
function [steady_state_value, steady_state_time, settling_time] = analyzeStepResponse(sys)
% Plot step response
figure;
[y, t] = step(sys);
plot(t, y);
title('系统的单位阶跃响应');
xlabel('时间 (秒)');
ylabel('输出');
% 计算稳态值
steady_state_value = y(end);
% 计算稳态时间
tolerance = 0.02; % 2% tolerance
steady_state_time = t(find(abs(y - steady_state_value) < tolerance * steady_state_value, 1, 'last'));
% 计算调节时间
settling_time = t(find(abs(y - steady_state_value) > tolerance * steady_state_value, 1, 'last'));
fprintf('稳态值: %.2f\n', steady_state_value);
fprintf('稳态时间: %.2f 秒\n', steady_state_time);
fprintf('调节时间: %.2f 秒\n', settling_time);
end
% Initialize parameters
P = 30; M = 1; N = 80; % 优化时域、控制时域和建模时域
ts = 1; % 采样周期
k_step = 150;
times = zeros(1, k_step);
R = 2 * eye(M); % 控制权矩阵
Q = 9 * eye(P); % 误差权矩阵
h = 0.4 * ones(N, 1);
h(1) = 1;
% Create transfer function
den = conv([20, 1], [5, 1]); % Denominator: (20s + 1)(5s + 1)
num = 2.69 * [-6, 1]; % Numerator: 2.69(-6s + 1)
order = length(den);
sys = tf(num, den, 'InputDelay', 1.5); % 建立传递函数,考虑纯滞后
[steady_state_value, steady_state_time, settling_time] = analyzeStepResponse(sys);
% Discretize the system
sysd = c2d(sys, ts);
[numd, dend] = tfdata(sysd, 'v');
[a, ~] = step(num, den, ts:ts:N*ts); % 获得模型向量a
% Initialize variables for DMC
S = diag(ones(1, N-1), 1); S(N, N) = 1; % 移位矩阵S
yr = 1; % 期望输出
dum = zeros(M, 1); % 优化变量
du = 0; % 控制增量
yn0 = zeros(N, 1); % 前一时刻预测输出
yn1 = zeros(N, 1); % 当前预测输出
yp0 = zeros(P, 1); % 优化输出
us = zeros(1, k_step); % 实际控制量
ys = zeros(1, k_step); % 实际输出
yk_history = zeros(order-1, 1);
uk_history = zeros(order-1, 1);
% Build dynamic matrix A
A = zeros(P, M);
for i = 1:M
A(i:P, i) = a(1:P-i+1);
end
% Calculate control gain
c = zeros(M, 1); c(1) = 1;
d = c' * inv(A' * Q * A + R) * A' * Q;
d = d'; % 控制增益
% Perform DMC simulation
times(1) = ts;
ys(1) = 0;
ek = ys(1) - yn1(1);
yn0 = S * (yn1 + h * ek); % 预测值校正
yp0 = yn0(1:P);
du = d' * (yr - yp0); % 计算这一时刻控制增量
us(1) = 0 + du; % 施加控制增量,得到实际控制量
uk = us(1);
uk_history(1) = uk;
yn1 = yn0 + a(1:N) * du; % 得到施加控制增量后的预测输出
for k = 2:k_step
times(k) = k * ts;
ys(k) = -dend(2:end) * yk_history + numd(2:end) * uk_history; % 得到系统的实际输出
yk_history(2:end) = yk_history(1:end-1);
yk_history(1) = ys(k);
ek = ys(k) - yn1(1); % 计算偏差
yn0 = S * (yn1 + h * ek); % 预测值校正
yp0 = yn0(1:P);
du = d' * (yr - yp0); % 计算这一时刻控制增量
us(k) = us(k-1) + du; % 施加控制增量,得到实际控制量
uk_history(2:end) = uk_history(1:end-1);
uk_history(1) = us(k);
yn1 = yn0 + a(1:N) * du; % 得到施加控制增量后的预测输出
end
% Plot results
figure
subplot(1, 2, 1);
plot(times, ys');
title('输出曲线');
subplot(1, 2, 2);
stairs(times, us');
title('控制量变化曲线');
其他算法 ¶
GPC——基于参数模型的广义预测控制 ¶
Generalized Predictive Control
SSC——基于状态空间模型的预测控制 ¶
State-Space Predictive Control
MAC——基于有限脉冲响应的模型算法控制 ¶
Model Algorithm Control
Papers & Applications¶
MPCC - Model Predictive Contouring Control¶
但在无人驾驶方程式大赛中,走赛道中心线显然不是最优路线,在不依靠路径优化的情况下,如何走出最短的路线,这就是 MPCC 希望解决的。
他的核心思想就是车辆的行驶路程(Frenet 坐标系的 s)也放到 MPC 的状态量。例如,当前 s=1m,在预测域中,s = 1.1,s = 1.2,s = 1.3,s = 1.4,s = 1.5,在计算跟踪误差时,就可以根据 s 插值得到在每个步长下的期望参考点
[MPCC in FSAC | Casadi] 基于 MPCC 的无人系统控制设计思路 -CSDN 博客
MPC and MHE implementation in Matlab using Casadi - Workshop
CasADi is an open-source tool for nonlinear optimization and algorithmic differentiation.
自动驾驶 & RC 小车轨迹控制 ¶
有障碍物的轨迹控制 alexliniger/MPCC: Model Predictive Contouring Controller (MPCC) for Autonomous Racing

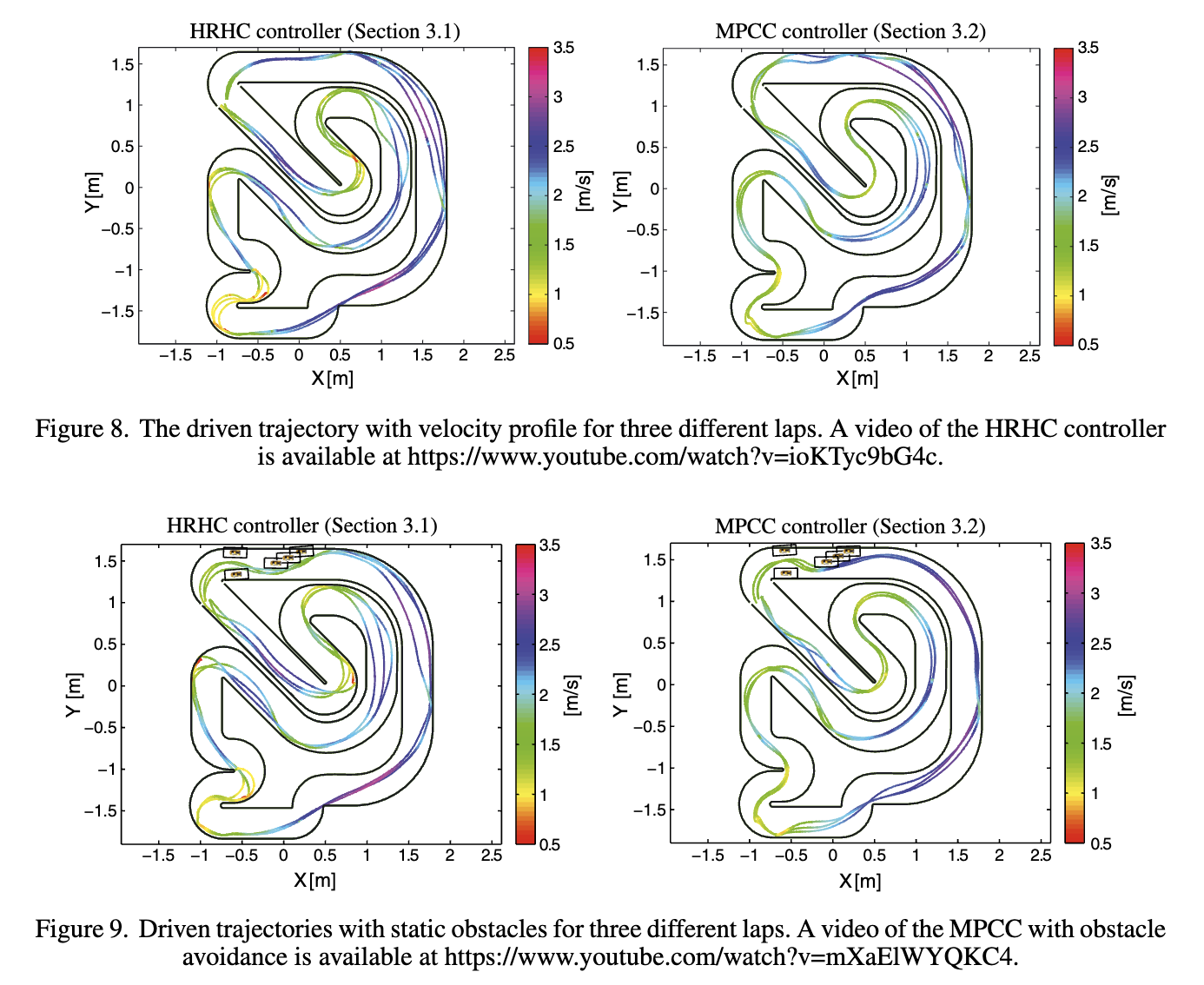
Optimization‐based autonomous racing of 1:43 scale RC cars - Liniger - 2015 提出了两种不同的控制方案。
- 第一个控制器采用两级结构,由路径规划器和用于跟踪的非线性模型预测控制器(NMPC)组成。
- 第二个控制器将这两个任务结合在一个非线性优化问题(NLP)中,遵循轮廓控制的思想。通过线性化获得的线性时变模型用于在每个采样时间构建控制 NLP 的局部近似,形成凸二次规划(QP
) 。生成的 QP 具有典型的 MPC 结构,障碍物规避通过基于动态规划的高级走廊规划器实现,该规划器根据对手的当前位置和赛道布局为控制器生成凸约束。 - 实验平台:控制性能通过使用 1:43 比例的 RC 赛车进行实验研究,这些赛车以超过 3 m/s 的速度行驶,并在后轮胎力饱和(漂移)的操作区域内运行。算法在嵌入式计算平台上以 50 Hz 的采样率运行,展示了基于优化的方法在自动驾驶中的实时可行性和高性能。
Related links - 论文中用到的RC小车是ミニッツRWD MR-04 レディセット シボレー コルベット C8.R ガンメタル / レッド 32356GMR - KYOSHO RC - RCFans论坛上有搭建轨道的教程RCFans论坛 【自建赛道】 完成 【制作全过程分享】 - Powered by Discuz! - 开源!手把手教你搭建阿克曼自动驾驶小车(上) - 知乎
机器人当中应用 ¶
- 非线性 MPC 用于容错控制
- Whole-body MPC 用于轮腿机器人
飞机轨迹控制 ¶

桨叶失效控制 ¶
Fault-Tolerant MPC 问题构建 :
- 正常飞行 :\(\bar{u} = T_{\max} 1_{4 \times 1}\)
- 单桨失效 :\(\bar{u}_{i} = \underline{u}_{i} = 0\)
飞行吊载控制 ¶