跳转至

01 | 基本概念

约 1786 个字 预计阅读时间 7 分钟

预置知识

和差化积 积化和差

基础公式

基本定义

随机过程

{ \(X(t);t\in T\) } 在 \(T\) 中取任一 \(t\) 的随机变量集合。

股票 243 个交易日的价格走向

样本函数

\(X(t)\) ，为 \(t\) 的函数。（所有随机变量取到可能出现的值）

股票一天的走势；三角函数振幅给定

  • 状态：给定 \(t_0\) ，\(X(t_0)\) 的与随机变量相关的值。
  • 状态空间：所有状态取值构成的集合。

分布函数

随机过程的分布函数

  • 一维分布函数
\[ F(t,x) = P\{X(t) < x\} \]
  • 二维分布函数
\[ F(s,t; x,y) = P\{X(s) < x, X(t) < y\}\]

数字特征

大部分随机过程的数字特征都是在和求期望打交道

  • 方差是用来度量单个随机变量的离散程度
  • 协方差则一般用来刻画两个随机变量的相似程度（相关性）

如何直观地理解「协方差矩阵」？ - 知乎

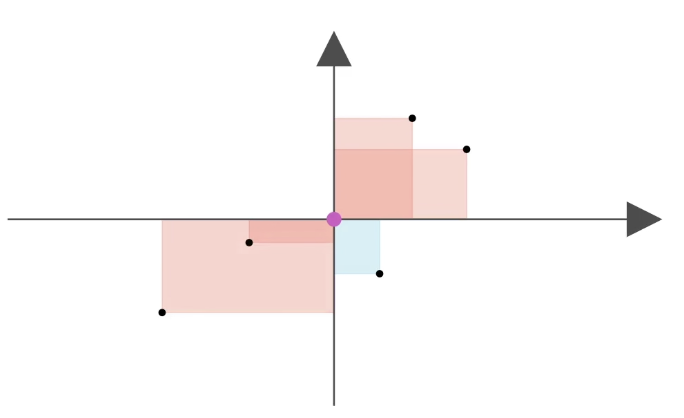
协方差：用与均值面积正负来刻画相关性 ( 一三象限是正相关，二四象限是负相关 ) 把原点看作\((\bar{x},\bar{y})\)，那么\(\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})\)就可以理解为这些矩形的面积了 图片出自如何通俗地解释协方差｜马同学图解数学_哔哩哔哩_bilibili

单个随机过程

  1. 均值函数 \(\mu(t) = E\big(X(t)\big)\)
  2. 方差函数 \(\sigma^2(t) = E\big(X^{2}(t)\big) - \mu^{2}(t) = C(t,t)\)
  3. 协方差函数 \(C(s,t) = E\big(X(s)X(t)\big) - \mu(s)\mu(t)\)
  4. 相关函数 \(R(s,t) = E\big(X(s)X(t)\big)\), 是协方差函数的第一项

理解自相关的例子：家族男性当中：父子身高的相关性、爷孙身高的相关性
自协方差：\(t\)和\(t+\tau\)的信号幅值变化相同，想找一个函数来去掉直流分量的影响

两个随机过程

  1. 互协方差函数 \(C_{XY}(s,t) = E\big(X(s)Y(t)\big) - \mu(s)\mu(t)\)
  2. 互相关函数 \(R_{XY}(s,t) = E\big(X(s)Y(t)\big)\)

自己和别人的两个时刻的对比 平稳随机过程的自相关和互相关（函数/系数）的性质 - 知乎

题型

求数字特征

需要搞清楚谁是随机变量

设随机过程 \(X(t)=At+B\) ，其中 \(A\)、\(B\) 独立同分布，\(P(A=1)=0.6\) ，\(P(A=-1)=0.4\) 。

(1) \(X(t)\) 的所有样本函数为 \(X(t)=t+1\) ；\(X(t)=-t+1\) ；\(X(t)=t-1\) ；\(X(t)=-t-1\)

(2) \(X(1)=A+B\) 的分布律为 \(P[X(1)=0]=0.48\) ； \(P[X(1)=2]=0.36\) ；\(P[X(1)=-2]=0.16\)

(3) { \(X(t);t∈T\) } 的均值函数为 \(E[X(t)]=tE(A)+E(B)=0.2t+0.2\)

(4) 自相关函数为

\[ \begin{aligned} R_X(t_1,t_2)&=E[X(t_1)X(t_2)]=E[(At_1+B)(At_2+B)]\\ &=t_1t_2E(A^2)+(t_1+t_2)E(AB)+E(B^2)=t_1t_2+0.04(t_1+t_2)+1 \end{aligned} \]

（∵ \(E(A)=0.2\) \(D(A)=0.96\) \(E(A^2)=E(B^2)=D(A)+E^2(A)=0.96+0.2^2=1\) ）

随机相位正弦波 \(X(t) = \alpha \cos(\beta t + \theta)\)，\(-\infty < t < +\infty\), 其中，\(\alpha, \beta\) 为常数，\(\theta\) 是在 \([0, 2\pi]\) 上均匀分布的随机变量，求 \(X(t)\) 的均值函数、方差函数、相关函数、协方差函数

解：

\(\theta\) 的概率密度为

\(f(\theta) = \begin{cases} \frac{1}{2\pi}, & 0 \leq \theta \leq 2\pi \\ 0, & \text{其他} \end{cases}\)

均值函数为：

\[ E(X(t)) = \int_{-\infty}^{+\infty} X(t) f(\theta) \, \mathrm{d}\theta = \int_{0}^{2\pi} \alpha \cos(\beta t + \theta) \frac{1}{2\pi} \, \mathrm{d}\theta = 0 \]
\[ \begin{align*} R(s, t) &= E(X(s) X(t)) = \int_{-\infty}^{+\infty} X(t) X(s) f(\theta) \, \mathrm{d}\theta\\ &= \int_{0}^{2\pi} \alpha^2 \cos(\beta t + \theta) \cos(\beta s + \theta) \frac{1}{2\pi} \, \mathrm{d}\theta \quad \rightarrow \text{积化和差}\\ &=\frac{\alpha^{2}}{2\pi}\frac{1}{2}\int_{0}^{2\pi}\cos\beta(t-s)+\cos(\beta(t+s)+2\theta)\mathrm{d}\theta\\ &=\frac{\alpha^{2}}{2}\cos\beta(t-s)\\ C(s,t)&=E\left(X(s)X(t)\right)-m(s)m(t)=R(s,t)\\ D(t)&=C(t,t)=\frac{\alpha^{2}}{2} \end{align*} \]

设随机过程 \(X(t)=V\cdot t\), 其中 \(V\) 是在 (0,1) 上服从均匀分布的随机变量

求过程 \(X(t)\) 的均值和自相关函数

解：

已知随机变量 \(V\) 的概率密度为：

\(f(v)=\begin{cases}1,v\in(0,1)\\0,\text{其他}\end{cases}\)

\[ \begin{aligned} &E\big(X(t)\big)=\int_{-\infty}^{+\infty}x(t)f(v)\:\mathrm{d}v=\int_{0}^{1}vt\:\mathrm{d}v=\frac{t}{2}\\ &R_{X}(t_{1},t_{2})=E\big(X(t_{1})Y(t_{2})\big)=E(Vt_{1}Vt_{2})=\int_{0}^{1}v^{2}t_{1}t_{2}\:\mathrm{d}v=\frac{t_{1}t_{2}}{3} \end{aligned} \]

设两个连续时间的随机相位信号 ,\(X(t)=\sin(w_{0}t+\Phi)\),\(Y(t)=\cos(w_{0}t+\Phi)\), 其中 \(w_0\) 为常数，\(\Phi\) 在 \((-\pi,\pi)\) 上服从均匀分布，求互协方差函数。

解：首先求两个信号的均值：

\(E(X(t))=E(\sin(w_{0}t+\Phi))=\int_{-\pi}^{\pi}\sin(w_{0}t+\Phi)\frac{1}{2\pi}\mathrm{d}\varphi=0\)

\(E(Y(t))=E(\cos(w_{0}t+\Phi))=\int_{-\pi}^{n}\cos(w_{0}t+\Phi)\frac{1}{2\pi}\mathrm{d}\varphi=0\)

互协方差函数为：

\[ C_{XY}(t_{1},t_{2})=R_{XY}(t_{1},t_{2})-E(X(t_{1}))E(Y(t_{2}))=R_{XY}(t_{1},t_{2}) \]

其中：

\[ \begin{aligned} R_{XY}(t_{1},t_{2})&=E(X(t_{1})Y(t_{2}))=E(\sin(w_{0}t_{1}+\Phi)\cos(w_{0}t_{2}+\Phi))\\ &=\int_{-\pi}^{\pi}\sin(w_{0}t_{1}+\Phi)\cos(w_{0}t_{2}+\Phi)\frac{1}{2\pi}\mathrm{d}\varphi\\ &=\frac{1}{4\pi}\int_{-\pi}^{\pi}\sin(w_{0}(t_{2}-t_{1}))+\sin(w_{0}(t_{1}+t_{2})+2\Phi)\mathrm{d}\varphi\\ &=\frac{1}{2}\sin(w_{0}(t_{2}-t_{1}))+\frac{1}{4\pi}\int_{-\pi}^{\pi}\sin(w_{0}(t_{1}+t_{2})+2\Phi)\mathrm{d}\varphi\\ &=\frac{1}{2}\sin(w_{0}(t_{2}-t_{1})) \end{aligned} \]

导函数的数字特征

设随机过程 \(X(t)\) 的均值与自相关函数为 \(m_{X}= 5\sin t\) , \(R_{X}( t, s) = 3\mathrm{e} ^{- 0. 5( s- t) ^{2}}\) 试求\(Y(t)=X^\prime(t)\)的均值和自相关函数

\[ \begin{aligned}&E\big(Y(t)\big)=\frac{\mathrm{d}}{\mathrm{d}t}E\big(X(t)\big)=5\cos t\\&R_{Y}(t,s)=\frac{\partial^2}{\partial s\:\partial t}R_X(t,s)\end{aligned} \]

随机过 \(X(t)=A\cos wt,Y(t)=(1-B)\cos wt\), 其中 \(A,B\) 同为均值为 2，方差为 \(\sigma^2\) 的高斯随机变量，\(A,B\) 统计独立，\(w\) 为非零常数。求两个随机过程的均值、互相关函数、互协方差函数

\[ \begin{aligned} &E\big(X(t)\big)=E(A\cos wt)=2\cos wt\\ &E\big(Y(t)\big)=E\big((1-B)\cos wt\big)=-\cos wt\\ &R_{XY}(t_{1},t_{2})=E\big(X(t_{1})Y(t_{2})\big)=E\big(A\cos wt_{1}\times(1-B)\cos wt_{2}\big)=-2\cos wt_{1}\cos wt_{2}\\&C_{XY}(t_{1},t_{2})=R_{XY}(t_{1},t_{2})-E\big(X(t)\big)E\big(Y(t)\big)=0 \end{aligned} \]

求分布函数

通过投掷一个硬币定义一个随机过程 :\(X(t)=\begin{cases} \cos\pi t, 出现正面 \\ 2t, 出现反面 \end{cases}\)(1) \(F\left(\frac{1}{2},x\right), F(1,x)\)(2) \(F\left(\frac{1}{2},1,x,y\right)\)

解 :

\(F\left(\frac{1}{2},x\right)\) 相当于是求 \(X\left(\frac{1}{2}\right)\) 的分布函数，这里要注意 \(X\left(\frac{1}{2}\right)\) 已经是一个随机变量

\(X\left(\frac{1}{2}\right)=\begin{cases} \cos\frac{\pi}{2}, 出现正面 \\ 1, 出现反面 \end{cases}\)

\(X\left(\frac{1}{2}\right)\) 0 1
\(\frac{1}{2}\) \(\frac{1}{2}\)

\(F\left(\frac{1}{2},x\right)=P\left\{X\left(\frac{1}{2}\right)<x\right\}=\begin{cases} 0, -\infty < x \leq 0 \\ \frac{1}{2}, 0 < x \leq 1 \\ 1, 1 < x < +\infty \end{cases}\)

\(F\left(\frac{1}{2},1,x,y\right)=P\left\{X\left(\frac{1}{2}\right)<x,X(1)<y\right\}\)

先求 \(X(\frac{1}{2}), X(1)\) 的联合分布律 :

\(X(\frac{1}{2})\) \(X(1) = -1\) \(X(1) = 2\)
\(0\) \(\frac{1}{4}\) \(\frac{1}{4}\)
\(1\) \(\frac{1}{4}\) \(\frac{1}{4}\)